ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Электроника
Добавлен: 23.10.2018
Просмотров: 8850
Скачиваний: 20

141
Сопротивления слоев коллектора и эмиттера здесь опущены,
так как в усилительной технике они несущественны. Однако
включение этих сопротивлений в схему не приводит ни к каким
затруднениям, так как через них протекают заданные токи, и,
значит, соответствующие напряжения легко рассчитать и доба-
вить к напряжениям на переходах.
4.4
Статические
параметры
транзистора
Нелинейные эквивалентные схемы, показанные на рис. 4.12,
используются при анализе режимов, связанных с большим сигна-
лом. При расчете малых переменных составляющих, характерных
для усилительной техники, эти схемы целесообразно линеаризо-
вать.
Возьмем за основу схему на рис. 4.12, б. Генератор постоян-
ного тока
0
K
I
исключим, поскольку нас интересуют переменные
составляющие, и введем вместо него дифференциальное сопро-
тивление коллекторного перехода
K
r . Эмиттерный диод также
заменим его дифференциальным сопротивлением
Э
r . Обратную
связь по напряжению отразим генератором э.д.с., включенным
последовательно с сопротивлением
Э
r .
Наконец, для учета частотных зависимостей включим па-
раллельно сопротивлениям
Э
r и
K
r барьерные емкости, а коэф-
фициент
α
будем считать операторной или комплексной величи-
ной. Тогда линейная эквивалентная схема транзистора будет та-
кой, как показано на рис. 4.13. Ее легко дополнить паразитными
емкостями, однако это редко необходимо.
Схема на рис. 4.13 хорошо отражает структуру транзистора
и содержит физически обоснованные параметры. Точка
1
Б
на
схеме называется внутренней базовой точкой в отличие от внеш-
него зажима базы.
142
α
N
I
1
α
i
I
2
r
б
r
ЭЭ
r
К
К
Б
I
Б
I
К
I
Э
Э
I
1
I
2
а
К
α
I
Э
Б
1
I
K0
r
б
Б
I
Б
I
К
I
Э
Э
б
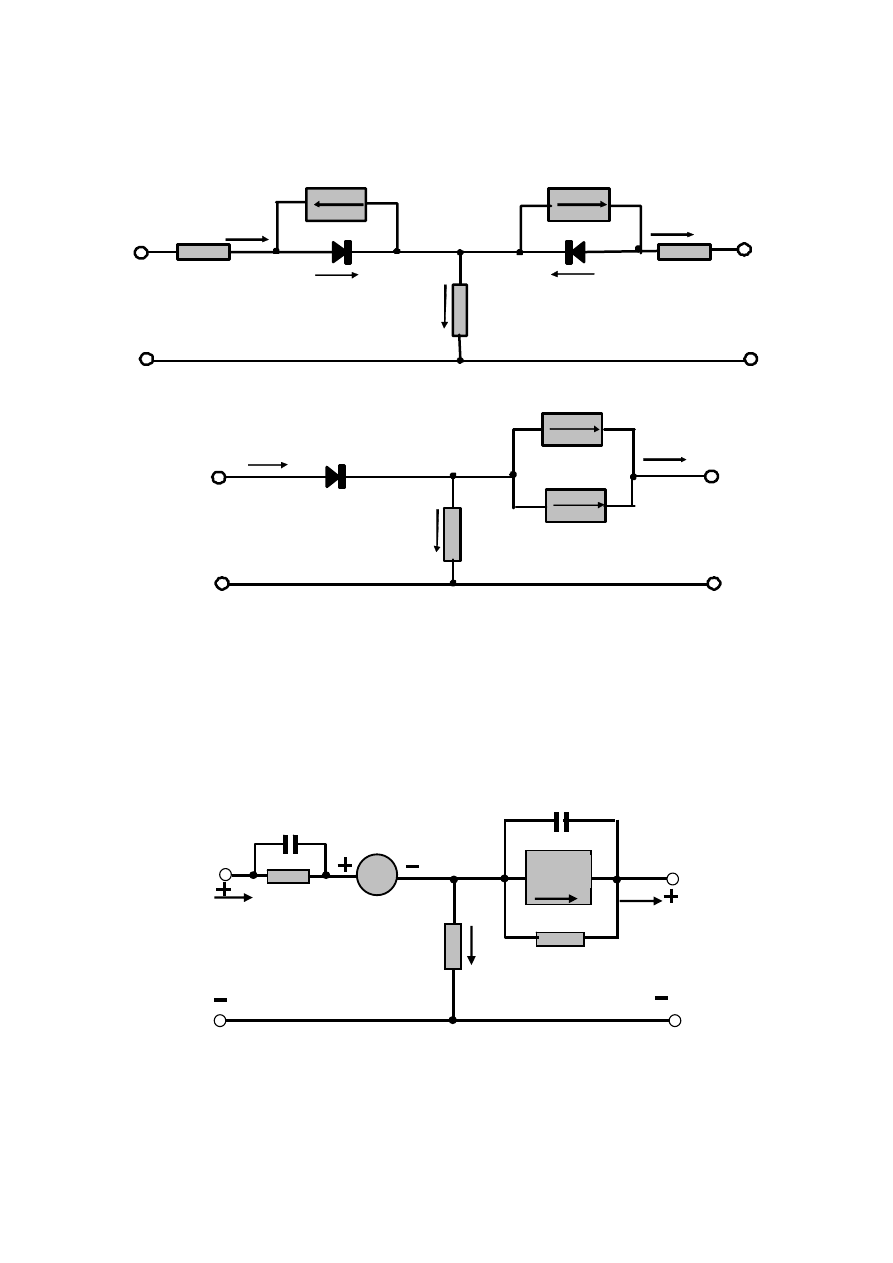
Рис. 4.12 — Эквивалентные схемы транзистора для постоянных
составляющих: а — общая схема с учетом сопротивлений слоев;
б — схема для нормального активного режима
I
Б
Б
I
К
C
Э
C
K
µ
ЭК
U
K
Б
1
К
Э
αIэ
r
Б
r
К
r
Э
I
Э
Рис. 4.13 — Эквивалентная схема транзистора
для переменных токов
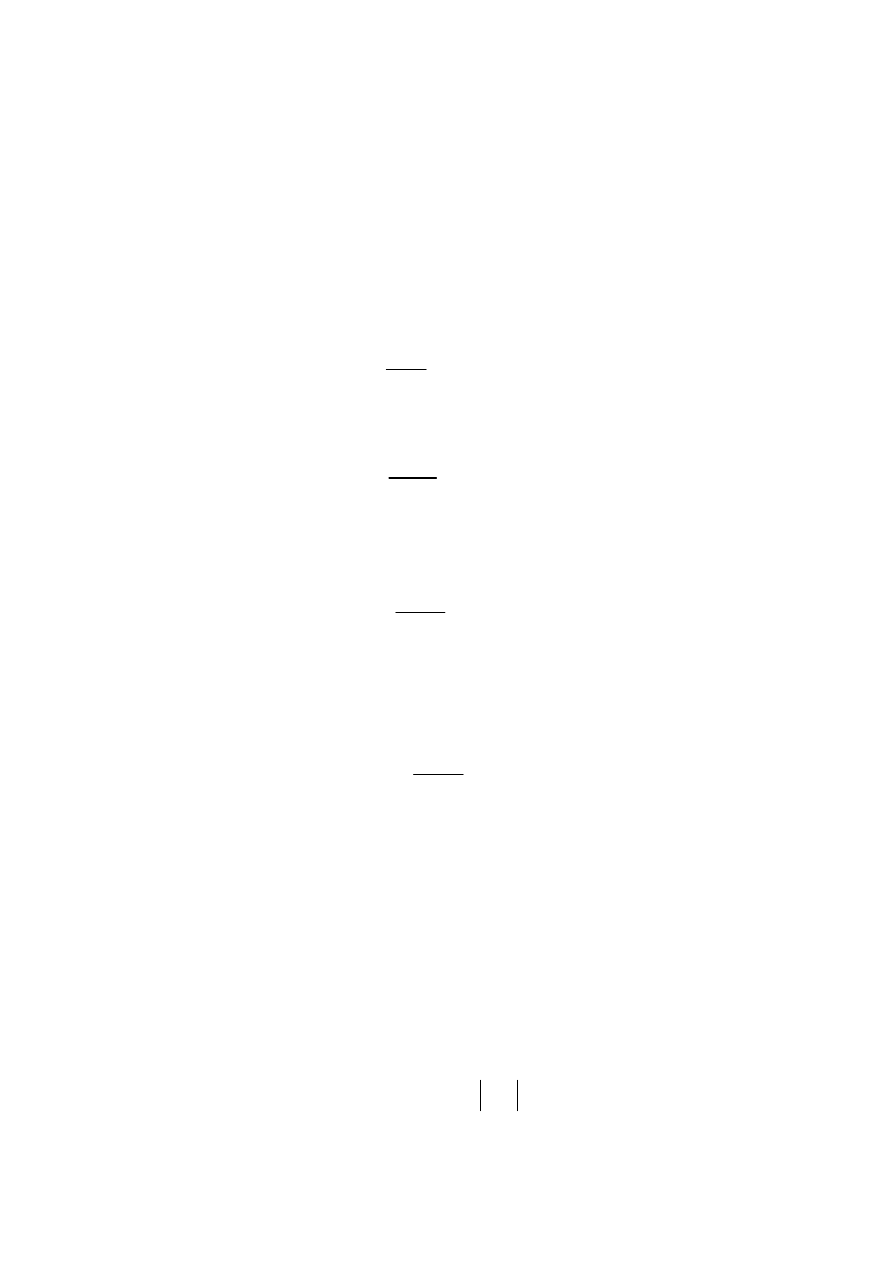
143
К числу основных параметров, необходимых при построе-
нии эквивалентной схемы транзистора (для переменных состав-
ляющих), относятся следующие: 1. Дифференциальный коэффи-
циент передачи эмиттерного тока при нормальном включении
N
α . В дальнейшем будем писать его без индекса N, так как ин-
версное включение относится к специальным случаям. Коэффи-
циент
α
определяется следующим образом:
Э
.
K
K
U
const
dI
dI
=
⎛
⎞
α = ⎜
⎟
⎝
⎠
(4.11а)
2. Дифференциальное сопротивление эмиттерного перехода
.
K
Э
Э
Э
U
const
dU
r
dI
=
⎛
⎞
= ⎜
⎟
⎝
⎠
(4.11б)
3. Дифференциальное сопротивление коллекторного пере-
хода
.
Э
K
K
K
U
const
dU
r
dI
=
⎛
⎞
= ⎜
⎟
⎝
⎠
(4.11 в)
4. Коэффициент внутренней обратной связи по напряжению,
характеризующий влияние коллекторного напряжения на эмит-
терный переход в связи с модуляцией толщины базы,
.
Э
Э
ЭК
K
I
const
dU
dU
=
⎛
⎞
μ
= ⎜
⎟
⎝
⎠
(4.11г)
5. Объемное сопротивление базы
Б
r . В отличие от преды-
дущих параметров сопротивление базы должно определяться
не для одномерной модели, а для реальной структуры транзисто-
ра. Ток базы протекает в направлении, перпендикулярном потоку
дырок, и, следовательно, необходимо учитывать реальную кон-
фигурацию базы, т. е. активную и пассивную ее части. Помимо
перечисленных дифференциальных параметров, важную роль
в работе транзистора играет тепловой ток
0
K
I
, который опреде-
ляется следующим образом:
0
0
(
)
;
Э
K
K I
I
I
=
=
K
T
U
>> ϕ
.

144
Коэффициент передачи эмиттерного тока. Величина
α
,
стоящая в формуле (4.8), в отличие от величины
α
в формуле
(4.11а) является интегральной, так как связывает не приращения
Э
I
∂ и
K
I
∂ , а полные токи
K
I и
Э
I .
0
.
K
K
ИН
Э
I
I
I
−
α
=
(4.12а)
Если бы коэффициент
α
не зависел от тока
Э
I , то, как сле-
дует из (4.8), дифференциальный коэффициент передачи был бы
равен интегральному значению. На самом деле он является функ-
цией эмиттерного тока, и поэтому, продифференцировав (4.8)
по току
Э
I , получим следующее соотношение:
.
ИН
ИН
Э
Э
d
I
dI
α
α = α
+
(4.12б)
Выразим коэффициент передачи тока эмиттера через физи-
ческие параметры транзистора. Эта задача будет линейной только
в том случае, если пренебречь зависимостью
( )
Э
I
α
, считая
ИН
α = α
. Поэтому в дальнейшем мы будем различать интеграль-
ный и дифференциальный коэффициенты передачи лишь тогда,
когда это принципиально необходимо. Коэффициент передачи
эмиттерного тока можно записать в следующем виде:
,
α = γχ
(4.13)
где
γ
— коэффициент инжекции дырок;
χ
— коэффициент пере-
носа дырок через базу, показывающий, какая доля инжектиро-
ванных дырок доходит до коллектора. На низких частотах коэф-
фициент инжекции в транзисторах не имеет специфики по срав-
нению с диодами и выражается известными формулами. Поэто-
му, прежде всего, проанализируем коэффициент переноса. Для
этого решим уравнение диффузии (1.39а) для стационарного ре-
жима
0
p
t
∂
=
∂
. В этом случае уравнение будет по форме таким
же, как (2.16); запишем его для полной концентрации
0
2
2
2
.
p
dp
p
dx
L
L
−
= −
(4.14)
Общее решение этого уравнения будет таким же, как (2.17),
а частным решением будет
0
p , поэтому

145
( )
1
2
0
.
x
x
L
L
p x
A e
A e
p
=
+
+
−
(4.15)
Граничные условия запишем, исходя из того, что в эмиттер-
ной цепи задан дырочный ток,
ЭР
Э
I
I
= γ , а на коллекторном пере-
ходе — напряжение
K
U
. Учитывая (1.34а) и (2.13а), получаем
при
0
x
=
и
x
w
=
соответственно:
0
;
ЭР
X
I
dp
dx
qDs
=
−
=
(4.16а)
( )
0
,
k
T
U
p w
p e
ϕ
=
(4.16б)
где S — как и раньше, площади переходов. Используя граничные
условия (4.16), определяем коэффициенты
1
A
и
2
A , входящие
в уравнение (4.15). После этого распределение концентрации
можно привести к следующему виду:
( )
0
1
1 .
K
T
U
ЭР
w
x
w
x
sh
сh
I
L
L
L
p x
p
e
w
w
qDS
ch
ch
L
L
ϕ
−
⎡
−
⎤
⎛
⎞
⎛
⎞
⎛
⎞
⎜
⎟
⎜
⎟
⎢
⎥
⎝
⎠
⎝
⎠
⎜
⎟
⎢
⎥
=
+
−
+
⎜
⎟
⎛ ⎞
⎛ ⎞
⎢
⎥
⎝
⎠
⎜ ⎟
⎜ ⎟
⎢
⎥
⎝ ⎠
⎝ ⎠
⎣
⎦
(4.17а)
При нормальном рабочем режиме (
0
k
U
< и
K
T
U
>> ϕ
),
а также при условии
w
L
<<
вторым членом в правой части
(4.17а) можно пренебречь. Тогда:
( )
.
ЭР
w
x
sh
I
w
L
p x
w
qDS
ch
L
−
⎛
⎞
⎜
⎟
⋅
⎝
⎠
=
⎛ ⎞
⎜ ⎟
⎝ ⎠
(4.17б)
Если пренебречь рекомбинацией в базе, положив
L
→ ∞
, что
выполняется далеко не всегда, то формула (4.17б) принимает вид
( )
1
.
ЭР
I
w
x
p x
qDS
w
⋅ ⎛
⎞
=
−
⎜
⎟
⎝
⎠
(4.17в)
Как видим, стационарное распределение дырок в тонкой ба-
зе близко к линейному, на что уже обращалось внимание выше
при анализе диода. Дифференцируя (4.17б) по х, умножая обе ча-
сти на
Dqs
−
и принимая во внимание, что
x
w
=
, получаем для
коллекторного тока выражение