ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Электроника
Добавлен: 23.10.2018
Просмотров: 8833
Скачиваний: 20
31
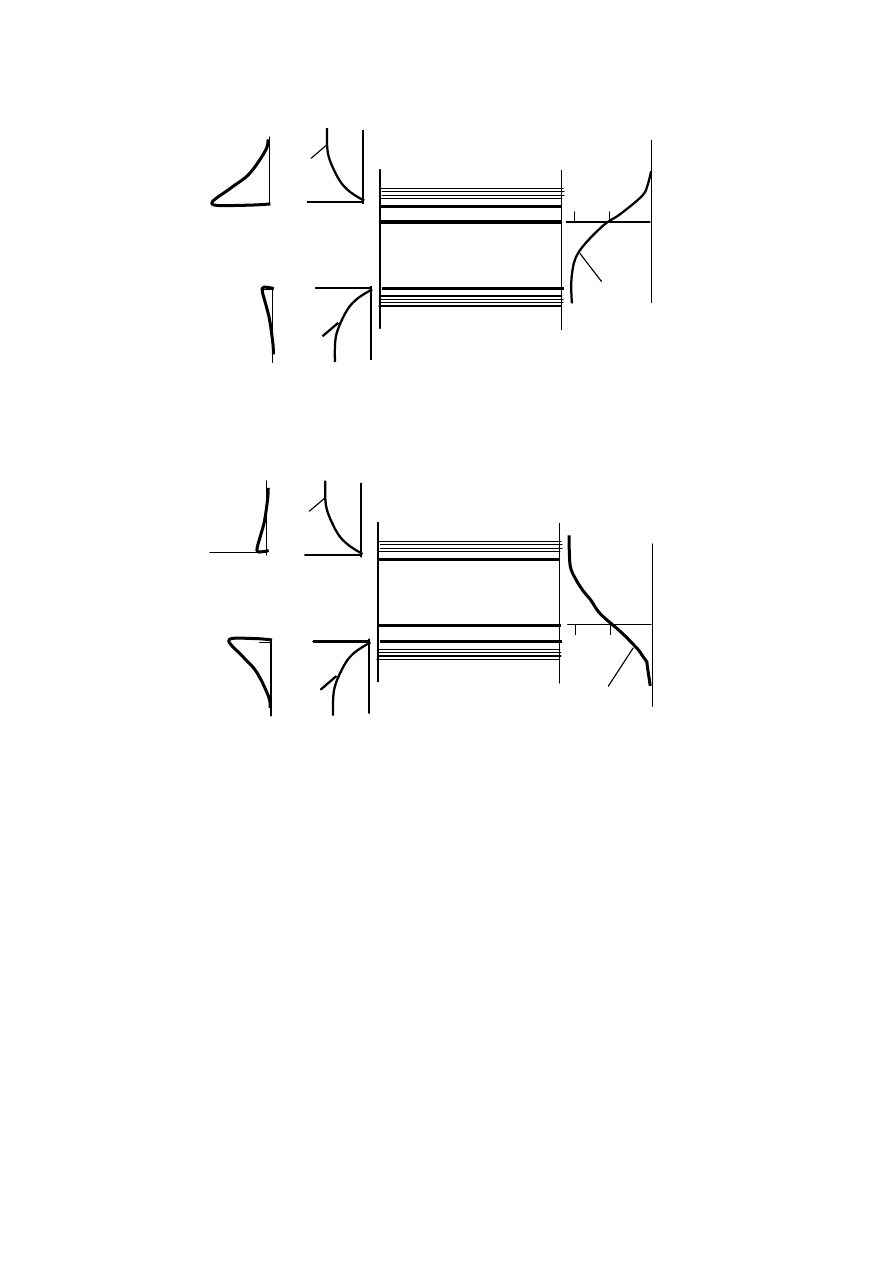
ϕ
V
ϕ
C
n
P
P
n
(ϕ
)
1 0,5
Запрещенная
зона
Валентная зона
Зона проводимости
ϕ
F
F
n
(ϕ
)
T
≠ 0
P
p
(ϕ
)
Рис. 1.10 — Плотность уровней энергии, функция вероятности
и концентрации носителей в примесном полупроводнике n типа
ϕ
V
ϕ
C
n
P
P
n
(ϕ
)
Запрещенная
зона
Валентная зона
Зона
проводимости
1 0,5
ϕ
F
F
p
(ϕ
)
T
≠ 0
P
p
(ϕ
)
P
p
(ϕ
)
Рис. 1.11 — Плотность уровней энергии, функция вероятности
и концентрации носителей в примесном полупроводнике p типа
В общем, виде условие нейтральности для единичного
объема можно записать в виде
(
)
*
*
0,
Д
а
p
N
n
N
+
− +
= (1.19
а
)
где
*
Д
N
и
*
а
N —
концентрации
ионизированных
доноров
и
ак
-
цепторов
.
Уравнение
(1–19
а
)
говорит
о
том
,
что
концентрация
частиц
,
несущих
положительный
заряд
(
дырки
и
ионизированные
доноры
),
равна
концентрации
электронов
и
ионизированных
ак
-
цепторов
.
Для
электронных
полупроводников
,
не
содержащих
акцепторов
,

32
*
.
д
n
N
p
=
+ (1.19
б
)
Для
дырочных
полупроводников
,
не
содержащих
доноров
,
*
.
a
p
N
n
=
+ (1.19
в
)
Перейдем
непосредственно
к
оценке
концентраций
свобод
-
ных
носителей
в
разных
типах
полупроводников
.
Рассмотрим
сначала
электронные
полупроводники
.
В
типичном
электронном
полупроводнике
выполняется
неравенство
n >
р
.
Кроме
того
,
бу
-
дем
считать
,
что
в
рабочем
диапазоне
температур
донорные
ато
-
мы
практически
полностью
ионизированы
,
т
.
е
.
*
Д
Д
N
N
=
.
Допу
-
стим
,
что
собственной
концентрацией
электронов
в
силу
того
,
что
их
концентрация
много
меньше
примесных
,
можно
прене
-
бречь
.
Тогда
из
соотношения
(1.19
б
)
получаем
концентрацию
свободных
электронов
.
Д
n
N
=
(1.20
а
)
Как
видим
из
1.20
а
,
концентрация
электронов
определяется
концентрацией
примеси
и
,
следовательно
,
не
зависит
от
темпера
-
туры
.
С
помощью
(1.16)
легко
получаем
концентрацию
свобод
-
ных
дырок
,
неосновных
носителей
,
которая
зависит
от
темпера
-
туры
в
силу
сильной
зависимости
от
температуры
собственной
концентрации
электронов
(
дырок
).
2
.
i
Д
n
p
N
=
(1.20
б
)
Наконец
,
из
(1.18
а
)
или
(1.13
а
)
находим
уровень
Ферми
в
типичном
электронном
полупроводнике
:
ln
ln
.
Д
Д
F
E
T
C
T
i
C
N
N
n
N
ϕ = ϕ + ϕ
= ϕ + ϕ
(1.20
в
)
Выражение
(1.20
в
)
позволяет
сделать
вывод
,
что
уровень
Ферми
лежит
тем
выше
,
чем
больше
концентрация
доноров
и
чем
ниже
температура
.
Вывод
можно
считать
справедливым
до
тех
пор
,
пока
снижение
температуры
не
приводит
к
уменьшению
числа
ионизированных
доноров
,
т
.
к
.
при
0
T
K
= °
уровень
Ферми
равен
F
E
ϕ = ϕ
.
Увеличение
температуры
приводит
к
росту
соб
-
ственной
концентрации
носителей
,
которая
становится
сравни
-
мой
с
концентрацией
примесей
,
затем
и
превышает
её
.
Проводи
-
мость
становится
преимущественно
собственной
.
С
изменением

33
типа
проводимости
значительно
изменяются
свойства
полупро
-
водниковых
материалов
и
приборов
,
выполненных
на
их
основе
.
Температура
,
при
которой
проводимость
становится
преимуще
-
ственно
собственной
,
определяет
допустимую
температуру
рабо
-
ты
полупроводникового
прибора
.
Необходимо
помнить
,
что
выражение
(1.20
в
)
получено
при
допущении
Д
i
N
n
>> .
Зависимость
от
температуры
обусловлена
в
основном
T
ϕ
,
т
.
к
.
отношение
концентрации
доноров
к
эффективной
плотности
со
-
стояний
остается
практически
постоянное
.
Простые
формулы
(1.20)
широко
используются
на
практике
.
Однако
следует
иметь
в
виду
,
что
они
действительны
в
ограниченном
температурном
диапазоне
:
с
понижением
температуры
степень
ионизации
доноров
уменьша
-
ется
и
принятое
равенство
*
Д
Д
N
N
=
становится
менее
строгим
.
Случай
дырочного
полупроводника
,
в
котором
р
> n,
нет
необходимости
рассматривать
столь
же
подробно
.
Главные
осо
-
бенности
акцепторной
примеси
видны
из
рис
. 1.11.
Если
акцеп
-
торы
полностью
ионизированы
и
температура
ниже
критической
,
то
вместо
формул
(1.20)
получаем
аналогичные
соотношения
,
ха
-
рактерные
для
ярко
выраженного
дырочного
полупроводника
:
;
a
p
N
=
(1.21
а
)
2
;
i
a
n
n
N
=
(1.21
б
)
ln
ln
.
a
a
F
E
T
V
T
i
V
N
N
n
N
ϕ = ϕ − ϕ
= ϕ − ϕ
(1.21
в
)
Весь
предыдущий
анализ
и
зонные
диаграммы
соответство
-
вали
однородным
полупроводникам
,
в
которых
примеси
распре
-
делены
равномерно
.
Разумеется
,
однородный
полупроводник
яв
-
ляется
некоторой
идеализацией
.
Более
того
,
часто
специально
со
-
здают
неоднородность
внутри
кристалла
в
виде
градиента
кон
-
центрации
примесей
,
что
придает
полупроводнику
новые
свой
-
ства
,
необходимые
для
работы
ряда
приборов
.
Посмотрим
,
како
-
вы
особенности
неоднородных
полупроводников
.
Пусть
,
напри
-
мер
,
в
полупроводнике
типа
n
концентрация
доноров
изменяется
от
1
Д
N
до
2
1
Д
Д
N
N
<
.
34
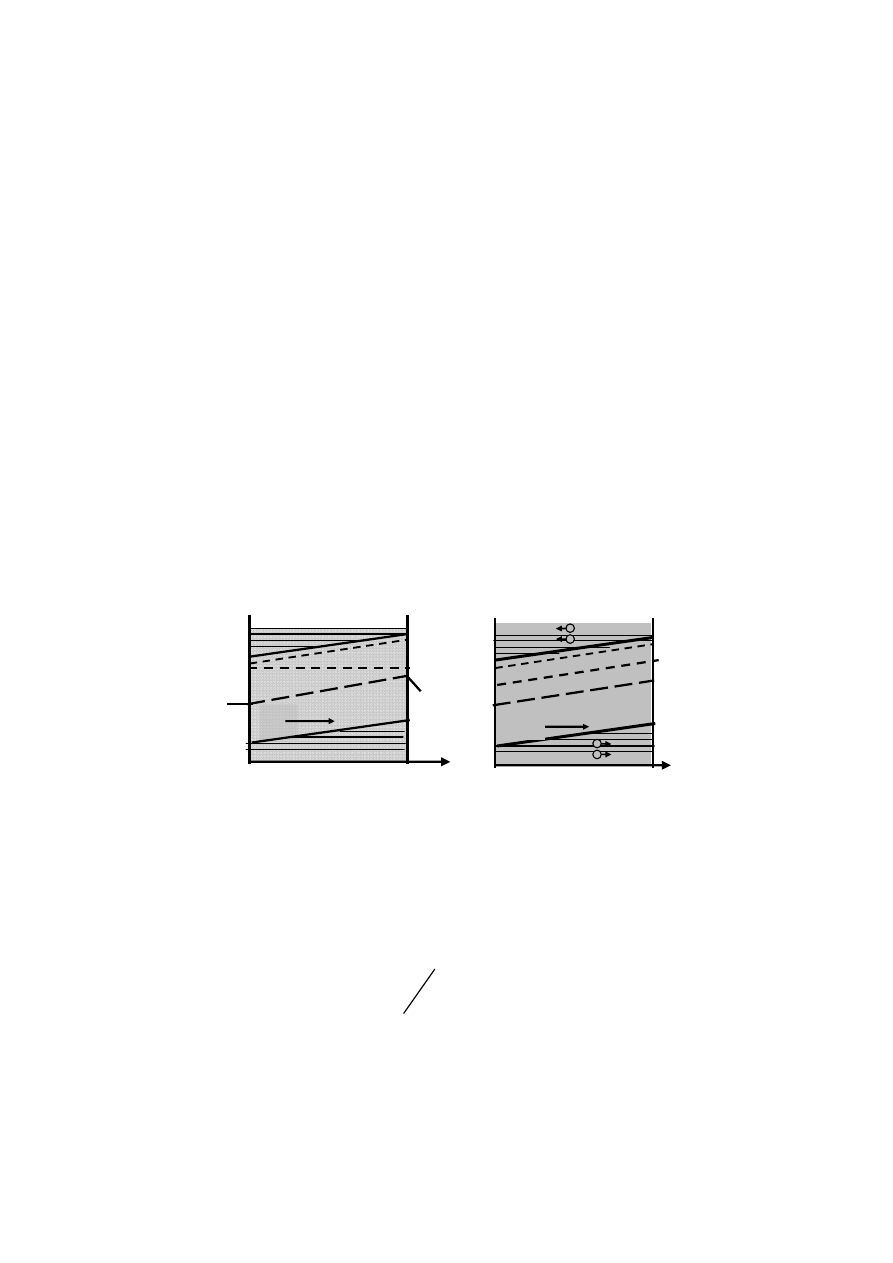
Поскольку в равновесной системе уровень Ферми
во всех ее частях одинаков, зонная диаграмма должна иметь
вид, как показано на рис. 1.12, а.
Учитывая
,
что
концентрация
доноров
,
а
следовательно
,
и
концентрация
электронов
слева
вы
-
ше
,
уровень
Ферми
у
левой
границе
полупроводника
должен
быть
ближе
к
«
дну
»
зоны
проводимости
.
Это
возможно
только
при
искривлении
зон
,
как
показано
на
рис
. 1.12,
а
.
Электростати
-
ческий
потенциал
Е
ϕ
вдоль
неоднородного
полупроводника
ме
-
няется
,
т
.
к
.
по
определению
это
потенциал
середины
запрещен
-
ной
зоны
.
Следовательно
,
в
неоднородных
полупроводниках
имеются
внутренние
электрические
поля
,
в
которых
возможен
дрейф
носителей
.
Однако
в
отсутствие
внешнего
поля
дрейфовые
потоки
носителей
равны
противоположно
направленным
диффу
-
зионным
потокам
,
которые
обусловлены
градиентом
концентра
-
ции
тех
же
носителей
.
Поэтому
результирующий
поток
отсут
-
ствует
и
соблюдается
больцмановское
равновесие
.
N
д2
N
д1
>
N
д
N
д
ϕ
F2
ϕ
F1
ϕ
E1
ϕ
E2
ϕ
F
ϕ
F
х
х
Е
Е
ϕ
E1
ϕ
E2
а
б
Рис 1.12 — Зонные диаграммы неоднородного полупроводника (а)
и однородного полупроводника при наличии внешнего
электрического поля (б)
Для
сравнения
на
рис
. 1.12,
б
показана
зонная
диаграмма
од
-
нородного
полупроводника
при
наличии
внешнего
электрического
поля
(
напряженность
E
d
E
dx
ϕ
=
та
же
,
что
и
на
рис
. 1.12,
а
).
Если
в
силу
условия
квазинейтральности
принять
концентрации
носи
-
телей
неизменными
вдоль
оси
х
,
то
будут
неизменными
и
хими
-
ческие
потенциалы
,
т
.
е
. «
расстояния
»
уровня
F
ϕ
от
краев
разре
-
шенных
зон
.
Тогда
согласно
(1.18)
имеет
место
градиент
уровня

35
Ферми
,
обусловленный
нарушением
равновесия
(
внешнее
элек
-
трическое
поле
вызывает
протекание
тока
).
Наличие
градиента
потенциала
Ферми
обусловливает
принципиальное
отличие
дан
-
ного
случая
от
предыдущего
(
рис
. 1.12,
а
),
и
прежде
всего
во
вто
-
ром
результирующий
ток
не
равен
нулю
,
несмотря
на
внешнее
сходство
«
перекошенных
»
зонных
диаграмм
.
Заметим
,
что
нали
-
чие
внутреннего
электрического
поля
в
общем
случае
не
означает
нарушения
условия
квазинейтральности
,
так
как
постоянное
или
почти
постоянное
поле
не
связано
с
существенными
объемными
зарядами
.
Все
сказанное
действительно
и
для
полупроводника
типа
р
с
учетом
расположения
уровня
Ферми
.
1.8
Подвижность
носителей
и
удельная
проводимость
Удельная
проводимость
любого
тела
зависит
не
только
от
концентрации
носителей
,
но
и
от
их
подвижности
в
электриче
-
ском
поле
.
Подвижность
носителей
по
определению
есть
их
средняя
направленная
скорость
в
электрическом
поле
с
напря
-
женностью
1
В
/
см
.
Соответственно
дрейфовую
скорость
можно
записать
в
виде
ДР
v
Е
= μ .
Постоянство
дрейфовой
скорости
но
-
сителей
в
однородном
поле
(
Е
=const)
специфично
для
твердого
тела
,
где
имеются
различные
«
препятствия
»
движению
.
В
вакуу
-
ме
,
где
таких
препятствий
нет
,
движение
заряженных
частиц
в
однородном
поле
равноускоренное
,
т
.
е
.
понятие
дрейфовой
скорости
отсутствует
.
Направленное
движение
носителей
в
твердом
теле
под
дей
-
ствием
поля
сочетается
с
их
хаотическим
(
тепловым
)
движением
.
*
3
/
.
T
V
kT m
=
(1.22)
Из
формулы
(1.22)
видно
,
что
тепловая
скорость
зависит
от
температуры
.
При
слабых
электрических
полях
дрейфовая
скорость
намного
меньше
тепловой
или
,
как
говорят
,
температура
носите
-
лей
определяется
температурой
кристаллической
решетки
.
В
этих
условиях
подвижность
можно
выразить
формулой
:
*
*
,
СР
СР
T
l
q
q
t
m
m V
μ =
=
(1.23)