ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Электроника
Добавлен: 23.10.2018
Просмотров: 11033
Скачиваний: 27

66
Анализ перехода в равновесном состоянии
Строгий анализ -
p n
переходов, в общем виде, весьма сло-
жен. Наиболее просто анализируется ступенчатый переход, рас-
смотренный в предыдущем разделе. Но даже в этом случае необ-
ходимы упрощающие допущения. В самом деле, если решать за-
дачу строго, т.е. исходить из структуры перехода, показанной на
рис. 2.3,
б
, то нужно учитывать распределение подвижных носи-
телей заряда и в переходе.
Задача анализа упрощается, если считать, что переход имеет
структуру, показанную на рис. 2.3,
в
, где концентрации подвиж-
ных носителей внутри перехода равны нулю и размеры перехода
малы, т.е. можно пренебречь процессами генерации и рекомби-
нации в переходе. Такое допущение вполне приемлемо. Во-
первых, в этой области доноры и акцепторы все ионизированы, а
во вторых, вследствие возникшей напряженности электрического
поля на переходе свободные заряды уносятся в нейтральные слои
соответствующих полупроводников.
Высоту равновесного потенциального барьера можно полу-
чить непосредственно из рис. 2.5,
а
:
0
,
n
p
F
F
Δϕ = ϕ − ϕ
(2.3)
где величины в правой части — потенциалы Ферми в полупро-
водниках до их объединения.
Из данного выражения следует, что чем ближе уровни Фер-
ми находятся к разрешенным зонам, тем больше диффузионный
потенциал. В первой главе мы показали, чем выше концентрация
примесей, тем ближе потенциал Ферми к потенциалам разрешен-
ных зон. Следовательно, изменяя концентрацию примесей, мож-
но управлять величиной диффузионного потенциала.
Максимальное значение потенциала Ферми для невырож-
денных полупроводников равно границам разрешенных зон по-
лупроводника. Максимальная высота потенциального барьера
перехода в невырожденных полупроводниках равна ширине за-
прещенной зоны полупроводникового материала.
Воспользуемся формулой (1.18а) и запишем эти потенциалы
через концентрации свободных электронов в слоях:
0
ln
p
p
F
T
E
i
n
n
ϕ = ϕ
+ ϕ ;

67
0
ln
n
n
F
T
E
i
n
n
ϕ = ϕ
+ ϕ ,
где индекс 0 соответствует равновесному состоянию концентра-
ций. Электрические потенциалы в обоих полупроводниках рав-
ны. Подставляя значения потенциалов Ферми в (2.3), придем к
выражению
0
0
0
ln
.
n
T
p
n
n
Δϕ = ϕ
(2.4а)
Если воспользоваться формулой (1.18б) или в выражении
(2.4а) заменить концентрации электронов концентрациями дырок
с помощью соотношения (1.16), то высота потенциального барье-
ра запишется следующим образом:
0
0
0
ln
.
p
T
n
p
p
Δϕ = ϕ
(2.4б)
Величину
0
Δϕ
иногда называют диффузионным потен-
циалом, поскольку эта разность потенциалов, во-первых, об-
разуется в результате диффузии носителей через переход и,
во-вторых, противодействует диффузионным потокам носи-
телей.
Еще одно название для величины
0
Δϕ — контактная раз-
ность потенциалов.
Выражая в любой из формул (2.4) концентрацию неоснов-
ных носителей (
p
n
или
n
p
) через концентрацию основных носи-
телей в том же слое с помощью соотношения (1.16) и используя
выражения (2.46), легко получить зависимость высоты равновес-
ного барьера от удельных сопротивлений слоев:
2
0
(
1)
ln
,
i
T
P n
b
b
ρ
+
Δϕ = ϕ
ρ ρ
(2.5)
где
n
p
b
μ
=
μ .
Для вычисления равновесной ширины потенциального
барьера
0
l
воспользуемся распределениями примесей и зарядов,
которые показаны на рис. 2.6.
Примем, что поле в переходе направлено вдоль оси
х
и от-
сутствует во всех других направлениях. При выполнении этого
68
допущения действительны уравнения Пуассона, в которых плот-
ности заряда в обеих частях ступенчатого перехода постоянны и
определяются концентрациями соответствующих ионизирован-
ных примесей (рис. 2.6,
б
):
p
a
qN
λ = −
;
n
Д
qN
λ = −
.
Из уравнений Пуассона следует, что плотность заряда в пе-
реходе прямо пропорциональна концентрации примесей. Учиты-
вая, что для ступенчатого перехода выполняется условие
a
Д
N
N
>>
, можно заключить
P
n
λ >> λ . Переход должен быть
нейтральным, т.е.
P P
n n
Q
Q
V
V
+
−
=
= λ
= λ
,
где
P
V
, Vn — объемы пространственного заряда в переходе, рас-
положенные в полупроводниках p и n типа. Учитывая условие
равенства зарядов в переходе, можно записать
P
V
<<Vn , т.е. пере-
ход сосредоточен в основном в высокоомном полупроводнике.
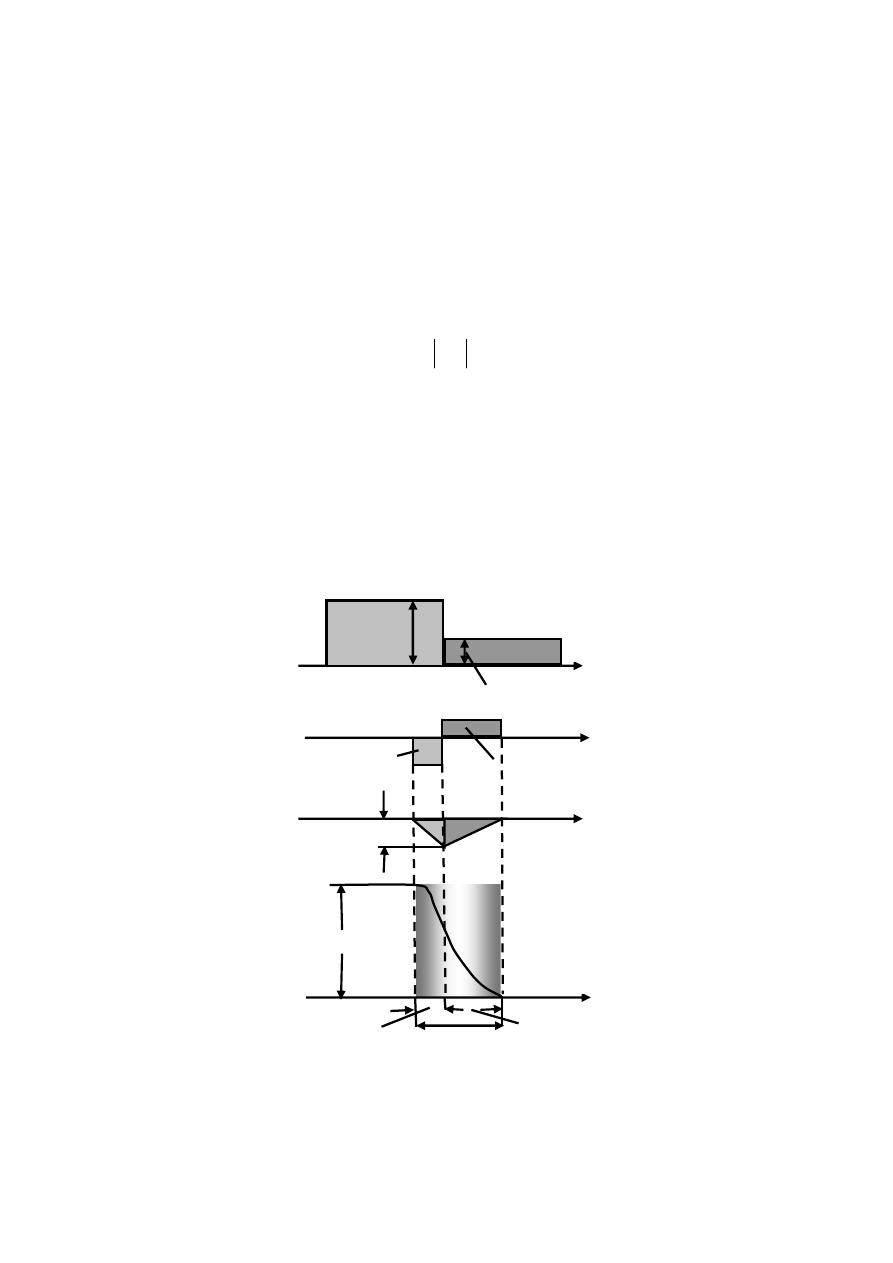
φ
ЕР
N
д
N
x
x
x
x
p-слой
n-слой
N
a
λ
Е
Е
макс
-qN
а
+qN
д
φ
Δφ
0
φ
Е
n
l
p
l
n
l
o
Рис. 2.6 — Распределение концентрации примесей (а),
плотности заряда (б), напряженности поля (в)
и потенциала (г) в ступенчатом
-
p n
переходе

69
Напряженность электрического поля равна нулю вне пере-
хода, если считать, что сопротивление перехода много больше
сопротивления нейтральных слоев полупроводников и используя
уравнения Пуассона, то напряженность в переходе изменяется по
закону, показанному на рис. 2.6,
в
, а выражения для них запишут-
ся в виде:
0
(
);
0;
а
p
p
qN
E
x
l
x
−
=
+
≤
ξ ξ
(2.6а)
0
(
);
0.
д
n
n
qN
E
l
x x
−
=
−
≥
ξ ξ
(2.6б)
При этом потенциал в пределах перехода будет изменяться
по квадратичному закону с точкой перегиба в месте излома кри-
вой
( )
E x
(рис. 2.6,
г
).
2
0
(
) ;
0;
2
a
p
Ep
p
qN
x
l
x
ϕ − ϕ = −
+
≤
ε ε
(2.7а)
2
0
(
) ;
0,
2
n
Д
n
E
n
qN
x l
x
ϕ − ϕ = −
−
≥
ε ε
(2.7б)
где
Ep
ϕ и
En
ϕ — электростатические потенциалы соответствую-
щих слоев вне перехода. Приравнивая значения напряженностей
на металлургической границе
0
x
= в выражениях (2.6а и 2.6б)
0
p
E
и
0
n
E
, получаем соотношение между шириной перехода в
слоях и концентрациями p и
n
.
.
p
Д
n
a
l
N
l
N
=
(2.8)
Для несимметричного перехода
A
Д
N
N
>>
, следовательно,
p
n
l
l
<< , а значит,
0
n
l
l
≈ , т.е. можно считать, что переход полно-
стью сосредоточен в высокоомном полупроводнике n.
Приравнивая
( )
0
p
ϕ
и
( )
0
n
ϕ
в выражениях (2.7а и 2.7б), ис-
пользуя соотношения
0
n
p
l
l
l
= + (2.8) и (2.3), можно получить за-
висимость между высотой барьера
0
Δϕ и шириной перехода
0
l
в
следующем общем виде:

70
0
0
0
2
1
1
(
).
Д
a
l
q
N
N
ξ ξΔϕ
=
+
(2.9а)
Для несимметричного перехода при
a
Д
N
N
>>
получаем:
0
0
0
2
.
Д
l
qN
ξ ξΔϕ
=
(2.9б)
Используя формулу (1.20в), выражение для ширины перехо-
да можно записать в виде:
0
2
0
2
ln
.
Д
a
T
i
Д
N N
n
l
qN
ε εϕ
=
(2.9
в
)
Из
выражения
(2.9
в
)
следует
,
чем
выше
концентрация
доно
-
ров
,
тем
меньше
ширина
перехода
,
т
.
е
.
влияние
высокоомного
полупроводника
более
существенно
по
сравнению
с
низкоомным
.
Увеличение
концентрации
доноров
приводит
к
увеличению
плотности
заряда
в
этом
слое
,
не
изменяя
плотности
заряда
в
низ
-
коомном
полупроводнике
.
Учитывая
,
что
заряды
в
переходе
сле
-
ва
и
справа
от
металлургической
границы
должны
быть
равны
по
абсолютной
величине
,
ширина
перехода
в
полупроводнике
n
уменьшится
.
Анализ перехода в неравновесном состоянии
Подключим
источник
напряжения
.
между
-
p
и
n -
слоями
.
Напряжение
нарушает
равновесие
в
системе
и
вызывает
изменение
величины
тока
.
При
этом
высота
потенциального
барьера
должна
измениться
,
так
как
при
равновесном
значении
0
Δϕ
потоки
носите
-
лей
через
переход
уравновешены
и
ток
отсутствует
.
Выше
было
показано
,
что
удельное
сопротивление
обедненного
слоя
на
не
-
сколько
порядков
выше
,
чем
удельное
сопротивление
основных
p -
и
n -
слоев
диода
.
Поэтому
внешнее
напряжение
почти
полностью
падает
на
переходе
,
т
.
е
.
изменение
высоты
потенциального
барьера
должно
быть
равно
величине
приложенного
напряжения
.
Когда
внешнее
напряжение
приложено
плюсом
к
p -
слою
,
высота
барьера
уменьшается
(
рис
. 2.7, а)
и
становится
равной
:
0
.
U
Δϕ = Δϕ − (2.10)