ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Электроника
Добавлен: 23.10.2018
Просмотров: 11037
Скачиваний: 27

76
дет иметь повышенное сопротивление, а граничный слой на рис.
2.9,
б
обогащается электронами и будет иметь пониженное со-
противление по сравнению с равновесным состоянием. Значит,
такая полярность будет обратной для контактов на рис. 2.9,
а
и
прямой для контактов на рис. 2.9,
б
.
Если изменить полярность приложенного напряжения, то по
аналогичным причинам сопротивление граничного слоя на рис. 2.9,
а
понизится и контакты будут работать в прямом направлении, а
сопротивление граничного слоя на рис. 2.9,
б
повысится, т.е. сис-
тема будет работать в обратном направлении.
Таким образом, контакты на рис. 2.9,
а
и
б
хотя и не обеспе-
чивают инжекции, но обладают вентильными свойствами и лежат
в основе диодов Шоттки. Принципиальное отличие таких контак-
тов от системы с образованием p-n перехода заключается в том,
что ток обусловлен основными носителями, подвижность кото-
рых значительно выше неосновных. Кроме того, отсутствие ре-
жима инжекции не приводит к накоплению и рассасыванию из-
быточных носителей заряда. Два этих фактора способствуют су-
щественному повышению быстродействия в диодах Шоттки.
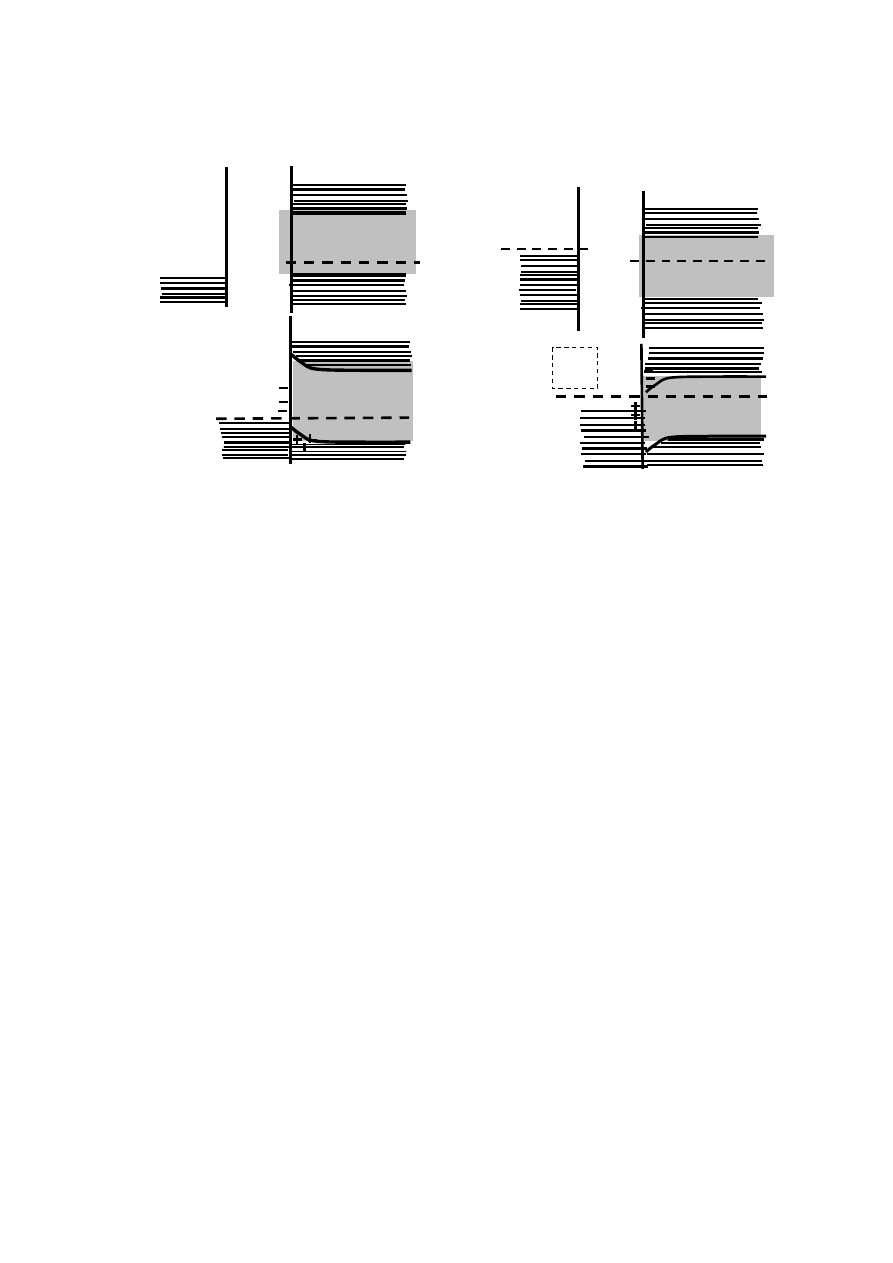
Иная картина получается тогда, когда для контакта металла
с полупроводником p -типа имеет место соотношение
Fm
Fp
ϕ
< ϕ ,
а для контакта металла с полупроводником
n
-типа — соотноше-
ние
Fm
Fn
ϕ
> ϕ . В этих случаях искривление зон в полупроводни-
ках получается обратным по сравнению с тем, какое показано на
рис. 2.9,
а
и
б
, т.е. граничные слои оказываются не обедненными,
а обогащенными основными носителями (рис. 2.10). Соответст-
венно, удельные сопротивления граничных слоев оказываются
ниже, чем у основных слоев полупроводника вдали от границы,
так что наличие граничного слоя в системе малосущественно с
точки зрения ее суммарного сопротивления. Следовательно, ре-
зультирующее сопротивление системы близко к сопротивлению
основного слоя полупроводника и почти не зависит от полярно-
сти и величины внешнего напряжения. Такие контакты называют
омическими, или невыпрямляющими. Невыпрямляющие контак-
ты являются основой омических контактов.
77
ϕ
FM
ϕ
Fn
ϕ
FM
Полупроводник
n-типа
Запрещенная
зона
металл
ϕ
F
ϕ
Fp
Полупроводник
p-типа
Запрещенная
зона
металл
ϕ
F
а
б
Рис. 2.10 — Зонные диаграммы невыпрямляющих контактов металла
с полупроводником: а — контакт с полупроводником
p
-типа;
б — контакт с полупроводником
n
-типа
2.4
Анализ
идеализированного
диода
Несмотря на то, что диод представляет собой один из про-
стейших полупроводниковых приборов, процессы, происходящие
в нем, достаточно сложны. Для того чтобы выяснить основные
параметры и характеристики диода, проведем сначала упрощен-
ный анализ, а затем в последующих параграфах уточним полу-
ченные результаты.
Исходные предпосылки
. Будем, как и раньше, считать -
p n
переход несимметричным и p -слой значительно больше легиро-
ванным, чем
n
-слой. При этом, как известно, инжекция и экс-
тракция носят односторонний характер, а значит, можно сосредо-
точить внимание на анализе процессов в базе и результаты анали-
за распространить на аналогичные, но менее существенные про-
цессы в эмиттере.
Анализ существенно упрощается, если принять следующие
допущения, а в дальнейшем ввести уточнения.
1. Слой базы является ярко выраженным электронным по-
лупроводником. Это значит, что вместо «объединенного» элек-

78
тронно-дырочного уравнения можно пользоваться уравнением
(1.33а) и положить
0
E
x
∂
=
∂
.
2. Концентрация дырок, инжектируемых в базу, невелика,
т.е. выполняется условие низкого уровня инжекции. При этом
полная концентрация дырок в базе
0
p
p
p
=
= Δ остается значи-
тельно меньше концентрации электронов
0
n
n
= . Следовательно,
можно пренебречь дрейфовой составляющей дырочного тока в
базе. По аналогичным причинам можно пренебречь дрейфовой
составляющей электронного тока в эмиттере. Соответственно
вместо уравнения непрерывности можно использовать уравнения
диффузии.
3. Падение напряжения в базе (а тем более в низкоомном
эмиттерном слое) значительно меньше внешнего напряжения, так
что последнее можно считать приложенным непосредственно к
переходу.
4. Ширина перехода настолько мала, что процессами гене-
рации и рекомбинации в области перехода можно пренебречь.
Это дает право считать электронные токи на обеих границах пе-
рехода одинаковыми; то же самое относится к дырочным токам.
Сразу же оговоримся, что это допущение очень часто не реализу-
ется, особенно для кремния и арсенида галлия, т.е. для полупро-
водниковых материалов с относительно большой шириной за-
прещенной зоны.
5. Обратные напряжения значительно меньше напряжения
пробоя, так что можно пренебречь предпробойными явлениями в
переходе.
6. Отсутствуют всякого рода поверхностные утечки, шунти-
рующие переход, а следовательно, и токи утечки, которые добав-
ляются к токам, обусловленным инжекцией и экстракцией.
Учитывая принятые допущения, работу диода можно опи-
сать следующим образом. При прямом смещении перехода кон-
центрация дырок на его базовой границе повышается, и эти избы-
точные дырки диффундируют в глубь базы. По мере удаления от
перехода концентрация дырок убывает и в установившемся ре-
жиме получается некоторое распределение избыточных дырок
( )
p x
Δ
(рис. 2.11,
а
). Инжекция дырок в базу нарушает ее ней-

79
тральность и вызывает приток избыточных электронов из внеш-
ней цепи. Эти электроны распределяются таким образом, чтобы
компенсировать поле дырок, т.е. накапливаются в той же облас-
ти, что и дырки. Поэтому кривые
( )
p x
Δ
и
n
Δ
(х)
оказываются
почти одинаковыми. Небольшая разница между этими кривыми
обусловлена различием подвижностей электронов и дырок (эф-
фект Дембера). В установившемся режиме в базе протекает диф-
фузионный дырочный ток, пропорциональный градиенту концен-
трации в каждой точке кривой
( )
p x
Δ
.
Так как полный ток диода должен быть одинаковым в лю-
бом сечении, то уменьшение диффузионного дырочного тока со-
провождается ростом электронной составляющей.
Структура полного тока рассмотрена нами раньше. Однако
величину полного тока удается вычислить без учета этой струк-
туры, если воспользоваться сделанными выше допущениями.
Действительно, учитывая допущения 2 и 4, можем для базовой
границы перехода записать:
( )
( )
( )
0
0
0
(0)
(
)
p
n
pдиф
nдиф
j
j
j
j
j
l
=
+
=
+
− ,
где координата x
l
= − соответствует эмиттерной границе. В одно-
мерном случае плотность тока
( )
0
j
сохраняется в любом сечении.
Реальные структуры полупроводниковых диодов и транзи-
сторов неодномерные, однако анализ проводится применительно
к одномерной модели (в данном случае применительно к модели,
показанной на рис. 2.8), после чего в случае необходимости де-
лаются те или иные поправки.
Таким образом, чтобы рассчитать ток диода, нужно, зная
величину приложенного напряжения, найти распределения дырок
в базе и электронов в эмиттере, определить градиенты этих рас-
пределений соответственно в точках
0
x
= и x
l
= − и затем с по-
мощью формул, известных нам из первой главы, получить ком-
поненты полного тока
.
(0)
рдиф
j
и
.
(
)
пдиф
j
l
− .
Решение диффузионного уравнения
. Чтобы получить ста-
тическую вольт-амперную характеристику диода, нужно найти
стационарное распределение дырок в базе. Для этого в уравнении
80
диффузии следует положить
0
p
t
∂Δ
=
∂
, после чего оно приводит-
ся к виду
( )
2
2
2
0,
d
p
p
dx
L
Δ
Δ
−
= (2.16)
где для простоты опущен индекс p при параметре
L
.
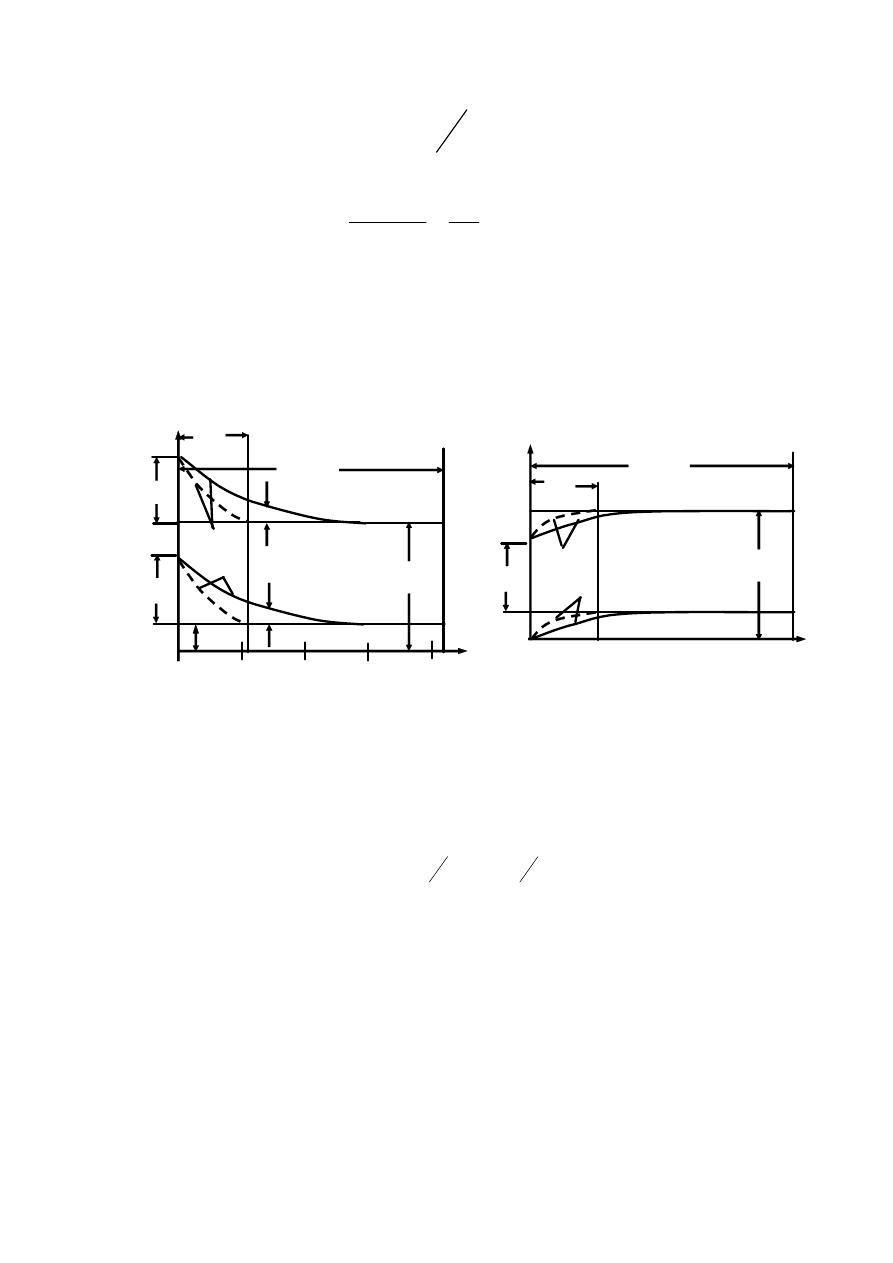
Поскольку в базе n
p
>> , кривые
( )
n x должны были бы
лежать намного выше, чем кривые
( )
p x . Чтобы этого избежать,
на рис. 2.11 сделан разрыв на оси ординат.
p
Δ
p(0)
Δ
p
p
0
Δ
n
n
p,n
w=L
Δ
n(0)
n
0
0 1 2 3
x/L
w>>L
а
Δ
p(0)
Δ
n(0)
p,n
w=L
Δ
n(0)
n
0
0 1 2 3
x/L
w>>L
p
n
б
Рис. 2.11 — Распределение носителей в диодах с толстой и тонкой базой:
а — при прямом смещении; б — при обратном смещении
Как известно, решением (2.16) является сумма двух экспо-
нент:
( )
1
2
.
x
x
L
L
p x
A e
A e
−
Δ
=
+
(2.17)
Для того чтобы в решении (2.17) определить коэффициенты
1
A и
2
A
, нужно знать граничные условия. В разделе 1.13 (разд.
«Монополярная диффузия») значение
( )
0
p
Δ
использовалось без
расшифровки, а толщина базы принималась бесконечно большой,
и соответственно полагалось
( )
0
p
Δ ∞ = . Теперь, учитывая конеч-
ные размеры базы, выразим граничную концентрацию
( )
0
p
Δ
че-
рез приложенное напряжение с помощью (2.14а):