Файл: Ядерная физика - уч. пособие Мухачев.pdf

26

Глава 2. Радиоактивность

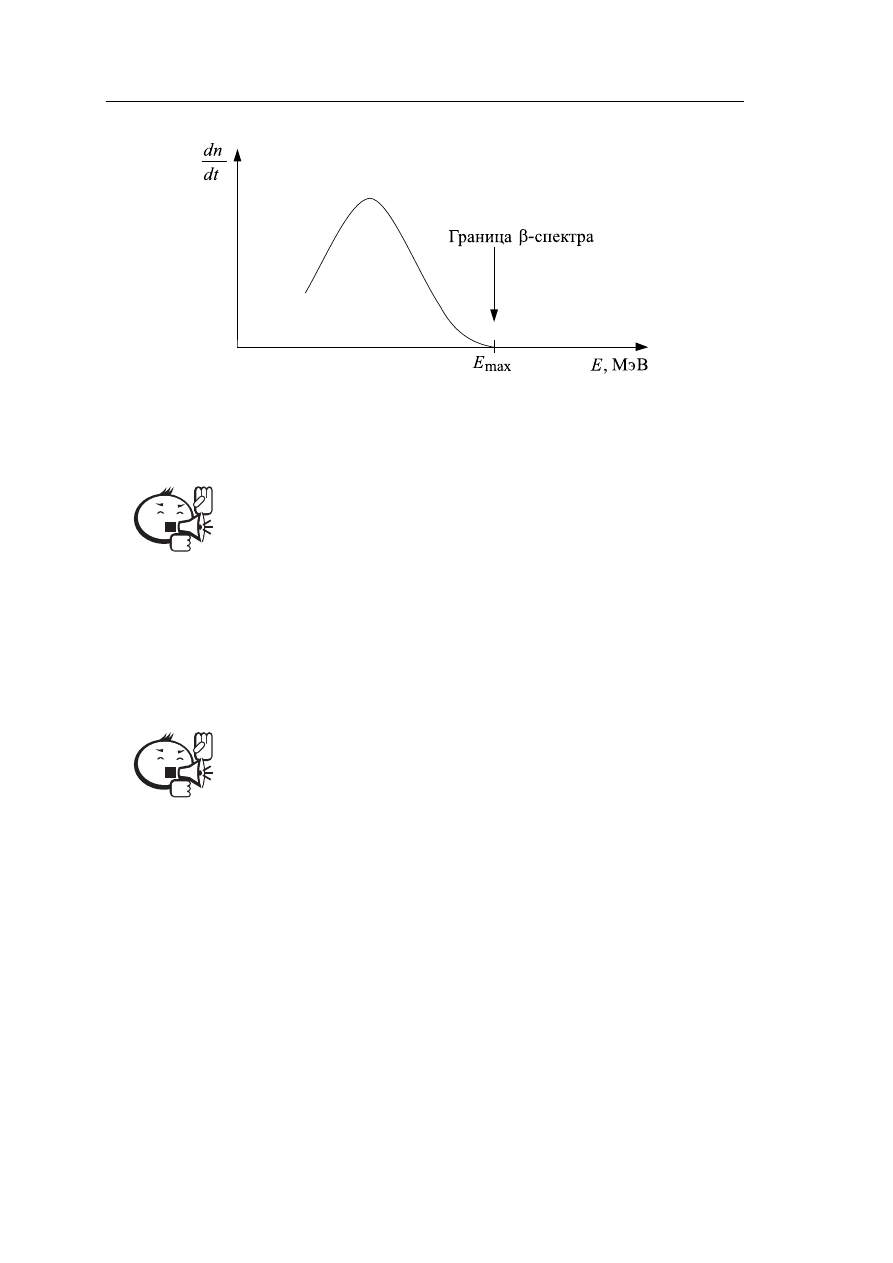
Рис. 2.4 – Примерная зависимость интенсивности вылетающих

электронов от их энергии

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

По предложению Э. Ферми (1901–1954 гг.) она была названа ней-
трино (нейтрончик); им же в 1933–1934 гг. была создана теория
β-распада, в которой нейтрино имел следующие характеристики:
энергия покоя равна нулю, электрический заряд равен нулю, спин
равен

~/2.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Непосредственное экспериментальное доказательство существования нейтри-

но было получено только в 1956 г. (В 1953 г. Рейнесом и Коуэном (США) было
зафиксировано, как потом выяснилось, антинейтрино, см. 4.4.4.)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Разгадка природы

β-распада позволила разгадать одно из фунда-

ментальных свойств элементарных частиц — рождение элементар-
ных частиц. В ядре нет ни электронов, ни нейтрино. Вылетая от-
туда, они рождаются при распаде нейтрона. Обе эти частицы не
входят в нейтрон, они именно рождаются.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Погибло представление об элементарных частицах как о неделимых кирпичи-

ках мироздания. Частицы могут рождаться и уничтожаться, но вот электрический
заряд не рождается и не исчезает, заряд вечен. Сформировался новый взгляд на
законы сохранения.

В целом теория

β-распада дала три важных следствия:

1) способность частиц рождаться и «исчезать»;

2) была «открыта» новая частица — нейтрино;

3) был открыт новый вид фундаментальных взаимодействий — слабое взаи-

модействие.

Позитронный

β

+

-распад. Схема распада:

A
Z

x

→

A

Z

−1

y

+

0
1

e

+ v

e

,

2.4 Виды распадов ядер

27

где v

e

— электронное нейтрино;

0
1

e — позитрон; v

e

,

0
1

e — античастицы по отношению

к тем, что рождаются при

β

−

-распаде. Пример реального

β

+

-распада:

13

7

N

→

13

6

C

+

0
1

e

+ v

e

.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Процесс

β

+

-распада происходит только у искусственных ядер

и протекает так, как если бы один из протонов превратился в ней-
трон, испустив позитрон и нейтрино. Для свободного протона
такой процесс невозможен, так как масса протона меньше мас-
сы нейтрона. Но в ядре протон может позаимствовать требуемую
энергию у других нуклонов.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Образовавшийся в результате распада ион превращается в нейтральный атом,

испуская один из электронов оболочки атома.

Электронный захват (K-захват). Этот вид распада заключается в том, что

ядро поглощает один из электронов 1-й, 2-й и даже 3-й оболочки (чаще все-таки
первой, K-оболочки). В результате один из протонов ядра превращается в нейтрон,
испуская при этом нейтрино:

p

+ e

−

→ n + v

e

.

Электронный захват сопровождается характеристическим рентгеновским излу-

чением.

Пример реального процесса:

40
19

K

+

0

−1

e

→

40
18

Ar

+ v

e

.

Отличительной чертой

β-распада является его внутринуклонное, а не внутри-

ядерное происхождение. Все виды

β-распада обусловлены следующими превраще-

ниями с участием нейтрино:

n

→ p + e

−

+ ˜v

e

,

p

→ n + e

+

+ v

e

,

p

+ e

−

→ n + v

e

.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

В этих процессах могут участвовать не только нуклоны, связанные
в ядре, но и свободные нуклоны. Вызывают эти процессы только
слабые взаимодействия [1–4].
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.4.3

γ-распад ядер

Этот вид распада состоит в испускании ядром

γ-кванта без изменения Z и A.

Энергия испускаемого

γ-кванта 0,01–5 МэВ, что значительно меньше энергии по-

коя ядра. Спектр испускаемых

γ-квантов дискретен благодаря дискретности энер-

гетического спектра внутриядерного движения (оболочечная модель). Механизм
γ-распада обусловлен взаимодействием отдельных нуклонов ядра с электромаг-
нитным полем. Тем не менее

γ-распад — явление внутриядерное, а не внутринук-

лонное, так как свободный нуклон может испустить

γ-квант только виртуально.

28

Глава 2. Радиоактивность

Вероятность испускания возбужденным ядром

γ-кванта в сильной степени за-

висит от величины спина начального и конечного состояния ядер. Если эти состо-
яния значительно отличаются по величине спина, то испускание

γ-кванта сильно

подавлено.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Это объясняется тем, что

γ-квант должен унести с собой боль-

шой момент импульса (

~), не унося большой энергии. Такие со-

бытия происходят очень редко, из-за чего времена жизни та-
ких

γ-активных ядер могут достигать макроскопических величин,

вплоть до нескольких часов, а иногда и больше. Столь долгоживу-
щие возбужденные состояния ядер называют изомерами. Один из
наиболее долгоживущих изомеров

236

Np — 5500 лет.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
С

γ-излучением конкурирует процесс, который называется внут-

ренней конверсией. Это явление заключается в том, что ядро
освобождается от энергии возбуждения, передавая ее непосред-
ственно одному из электронов атомной оболочки. Механизм явле-
ния состоит в испускании ядром

γ-кванта, который затем погло-

щается электроном оболочки. Электрон улетает или переходит
на возбужденный уровень, а его место занимает электрон внеш-
ней оболочки, при этом испускается фотон характеристического
рентгеновского излучения.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.4.4 Эффект Мёссбауэра

С

γ-излучением и поглощением γ-квантов ядрами, а именно с резонансным

поглощением, связано одно из крупнейших открытий в физике XX века — эффект
Мёссбауэра (Р. Мёссбауэр (1929–2011 гг.), открытие сделано 31 января 1958 г., Но-
белевская премия, 1961 г.).

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Резонансное поглощение — поглощение

γ-квантов такими же яд-

рами, какие являлись источником

γ-квантов.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Рассмотрим два неподвижных и одинаковых ядра, но одно находится в возбуж-

денном состоянии (источник), а другое — в стационарном состоянии (поглотитель).
Возбужденное ядро переходит в стационарное состояние и при этом испускает

γ-

квант (тот же фотон, только энергия его

∼ МэВ). При этом ядро испытывает отдачу

(в силу закона сохранения импульса

∣P

я

∣ = ∣P

γ

∣). Энергия перехода ядра из возбуж-

денного состояния в стационарное (

∆E) делится между ядром и γ-квантом:

∆E = cP

γ

+

P

2
я

2m

я

,

где P

2
я

/(2m

я

) — нерелятивистское выражение для кинетической энергии ядра.

2.4 Виды распадов ядер

29

Всегда выполняется условие

∆E ≪ m

я

⋅c

2

— выделяющаяся энергия много мень-

ше энергии покоя ядра. Подавляющую долю энергии уносит

γ-квант, поэтому с вы-

сокой точностью можно считать, что P

γ

≅ (∆E)/c. Следовательно, и P

я

≅ (∆E)/c.

Тогда

cP

γ

= ∆E −

∆E

2

2m

я

⋅ c

2

,

где

∆E

2

/(2m

я

⋅ c

2

) — энергия отдачи ядра. Именно на эту величину уменьшается

энергия

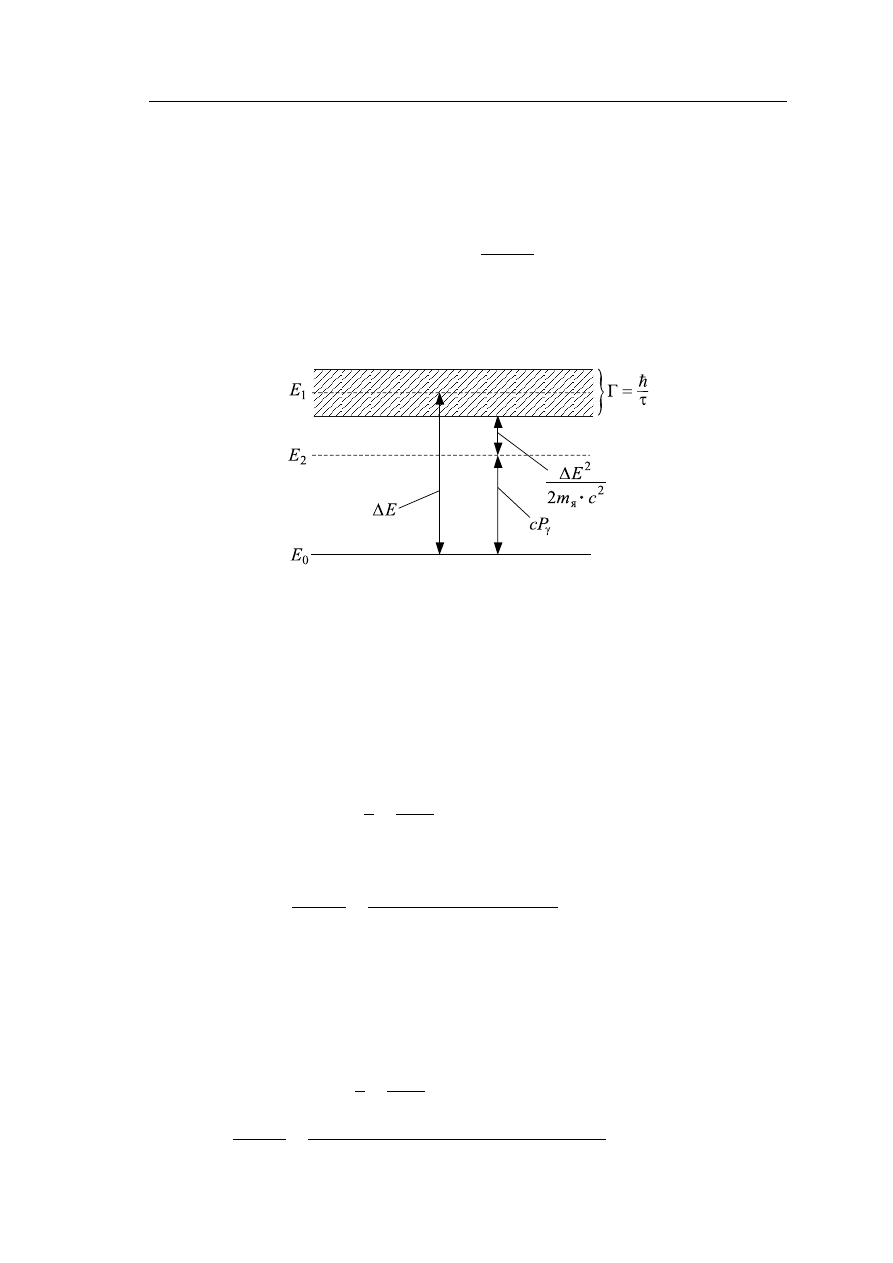
γ-кванта. Уменьшение энергии γ-кванта равносильно тому, что фотон об-

разовался не при переходе из состояния E

1

, а из состояния E

2

(рис. 2.5).

Рис. 2.5 – Схема, поясняющая уменьшение энергии

γ-кванта

Поэтому энергии

γ-кванта не хватает для возбуждения ядра-поглотителя, т. е.

для перевода его из E

0

в состояние E

1

. Спасти положение может естественная ши-

рина спектральной линии, т. е. неопределенность энергии возбужденного уровня
E

1

(Γ), в соответствии с соотношением неопределенности Γ ⋅ τ ⩾ ~, где τ — время

жизни возбужденного уровня. Если

Γ > [∆E

2

/(2m

я

⋅ c

2

)], то резонансное поглоще-

ние может наблюдаться.

Например, у атомов

τ ≅ 10

−8

c, энергия фотона

∆E ≅ 1 эВ, при этом

Γ =

~

τ

≅

10

−34

10

−8

≅ 10

−26

Дж

≅ 10

−7

эB.

Уменьшение энергии фотона для атома с A

= 50:

∆E

2

2m

я

⋅ c

2

≅

(1 эB) ⋅ 1,6 ⋅ 10

−19

2

⋅ 50 ⋅ 1,66 ⋅ 10

−27

⋅ 9 ⋅ 10

16

≅ 10

−11

эB.

Γ ≫ [∆E

2

/(2m

я

⋅ c

2

)], поэтому в атомах резонансное поглощение легко наблю-

дается.

Для ядер соотношение совсем другое. Например, для ядра

191

Ir (именно у этих

ядер Р. Мёссбауер впервые наблюдал резонансное поглощение)

τ ≅ 10

−10

c, энергия

возбуждения

∆E = 129 кэВ.

Γ =

~

τ

≅

10

−34

10

−10

≅ 10

−24

Дж

≅ 6 ⋅ 10

−6

эB.

∆E

2

2m

я

⋅ c

2

≅

(129 ⋅ 10

3

)

2

⋅ (1,6 ⋅ 10

−19

)

2

2

⋅ 191 ⋅ 1,66 ⋅ 10

−27

⋅ (3 ⋅ 10

8

)

2

⋅ 1,6 ⋅ 10

−19

≅ 5 ⋅ 10

−2

эB.

30

Глава 2. Радиоактивность

Γ ≪ [∆E

2

/(2m

я

⋅ c

2

)], и такое соотношение присуще всем ядрам, поэтому резо-

нансного поглощения ядер не наблюдалось.

Итак, резонансное поглощение

γ-квантов невозможно! Так думали все до 1958 г.

А если m

я

→ ∞? Как? Да «связать» его в твердом теле (аналогия с безоткатным

орудием). Никакой отдачи не будет. А чтобы не мешал эффект Доплера — охладить
образец до низких температур.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Испускание и поглощение

γ-квантов без явления отдачи импульса

и составляет сущность эффекта Мёссбауэра.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

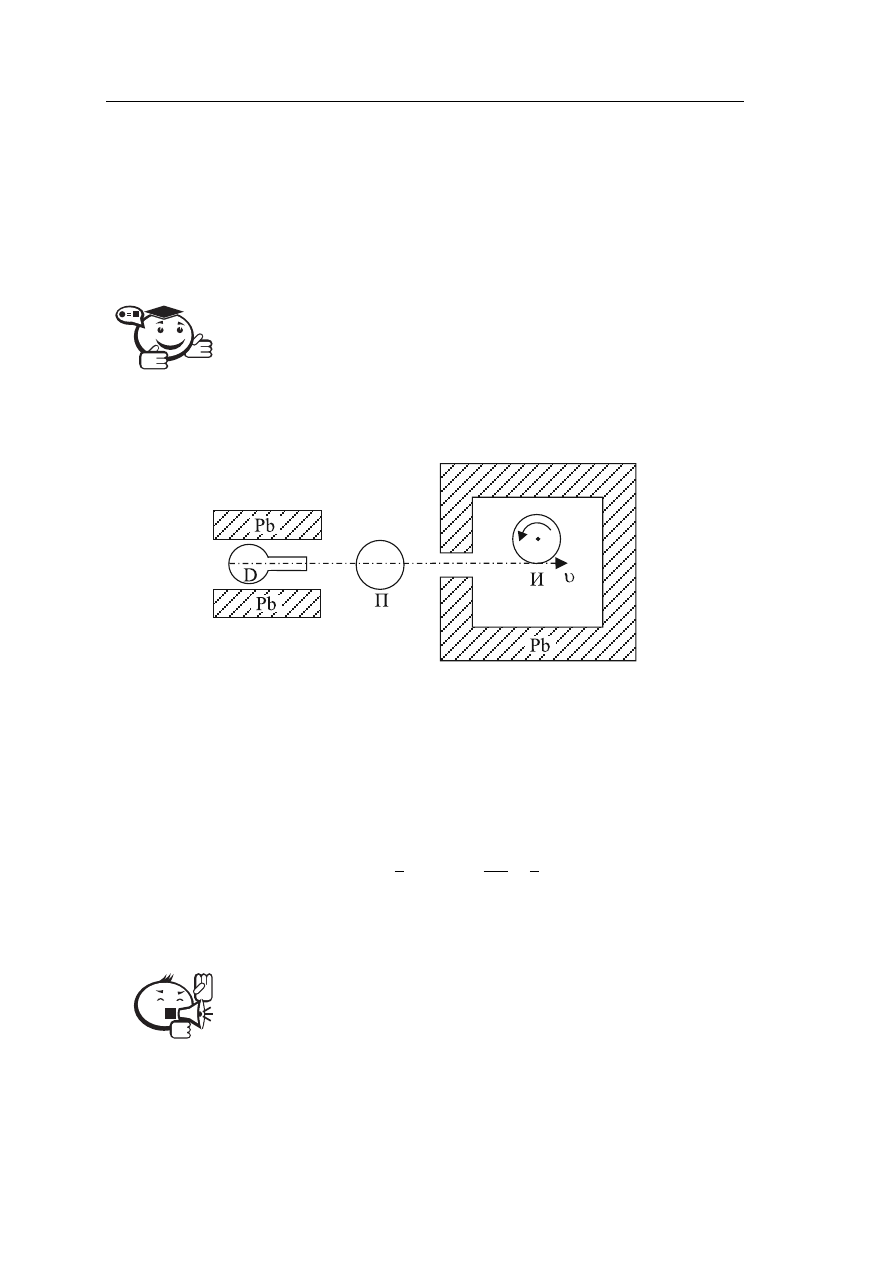
Поглотитель неподвижен, источник вращается на диске (у Мёссбауэра был па-

тефонный диск, рис. 2.6).

Рис. 2.6 – Схематическое изображение экспериментальной установки

для исследования эффекта Мёссбауэра:

И — источник, П — поглотитель, D — детектор

γ-квантов

Измеряется зависимость скорости счета

γ-квантов от величины и направления

скорости движения радиоактивного источника (рис. 2.7). При

υ ≠ 0 линии испус-

кания и поглощения сдвинуты относительно друг друга за счет эффекта Доплера.
При

υ ≪ c:

ω = ω

0

(1 +

υ

c

) или

∆ω

ω

0

=

υ

c

.

При

υ = 0 линии испускания и поглощения совпадают и происходит резонанс-

ное поглощение

γ-квантов; скорость счета γ-квантов резко падает.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Огромная важность этого открытия состоит в том, что эффект
Мёссбауэра позволяет измерять изменение энергии с огромной
точностью (относительная точность метода

≈ 10

−15

–10

−16

). Эффект

позволяет обнаружить даже ничтожное влияние, которое оказыва-
ет электронная оболочка атома на ядро.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .