ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Ядерная физика
Добавлен: 23.10.2018
Просмотров: 3817
Скачиваний: 10
2.2 Атомные часы. Радиоуглеродный метод измерения времени
21
Решение:
За время dt: dN
= N
0
⋅ dt − λN
0
dt, здесь
λ ≡ λ
2
.
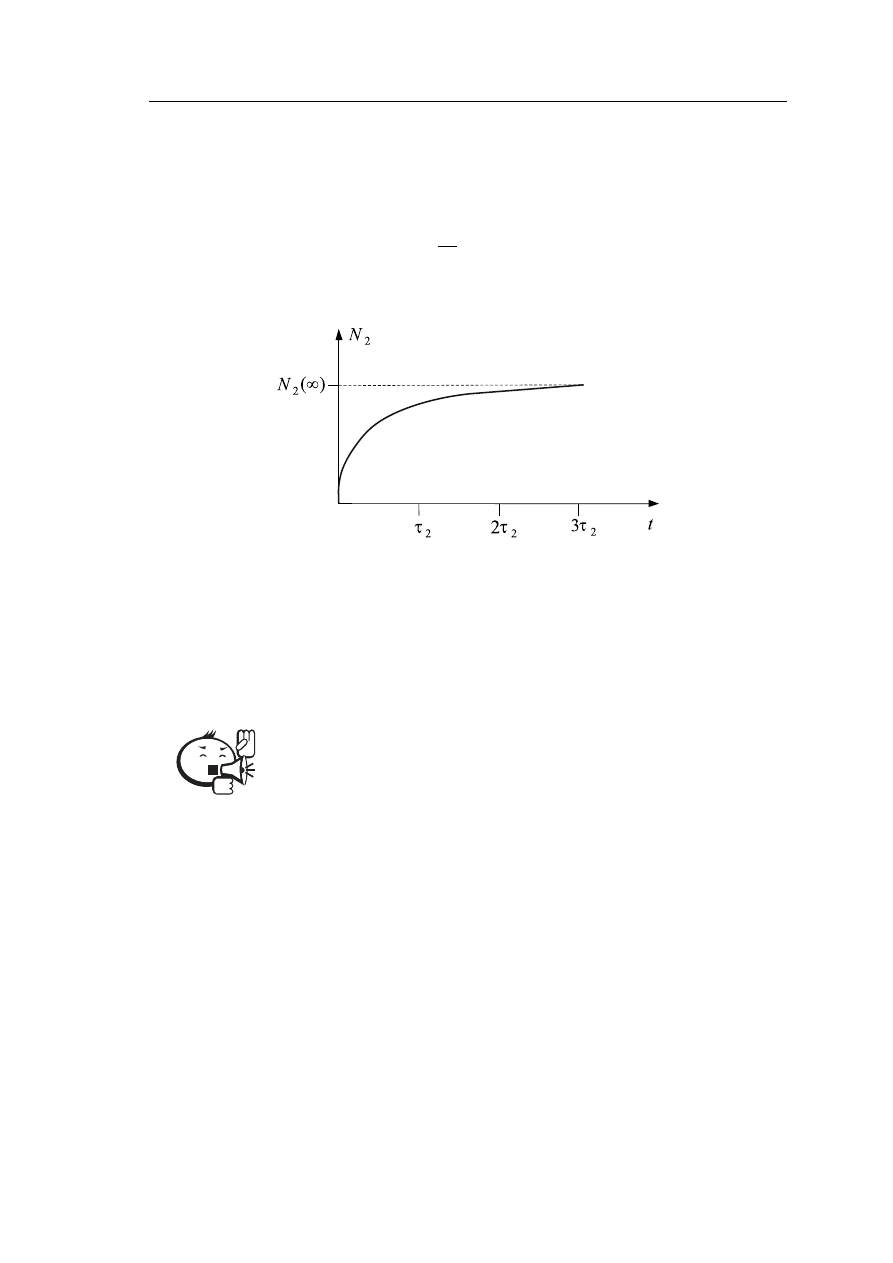
Решением этого дифференциального уравнения будет:
N
=
N
0
λ
(1 − e
−λt
).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Рис. 2.1 – Зависимость числа дочерних ядер от времени распада
2.2 Атомные часы. Радиоуглеродный метод
измерения времени
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Обычными физическими средствами невозможно ускорить или за-
медлить процесс распада ядер. Воздействовали давлением, темпе-
ратурой и т. д., но скорость распада оставалась постоянной. Эта
особенность позволяет использовать закон радиоактивного распа-
да в качестве часов для измерения длительных промежутков вре-
мени.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
В 1948 г. американский ученый У. Либби (1908 –1980 гг.) предложил радио-
углеродный метод, за который в 1960 г. получил Нобелевскую премию по химии.
Животные и растения поглощают нерадиоактивный углерод
12
C, а вместе с ним
и радиоактивный
14
C, образующийся в верхних слоях атмосферы под воздействи-
ем космических лучей. Можно считать, что космический фон не изменялся для
Земли в течение миллионов лет. Период полураспада
14
C T
= 5800 лет. Этот срок
много меньше времени жизни Земли, поэтому можно считать, что в земной ат-
мосфере установилось равновесие между
12
C и
14
C. Это соотношение одинаково
и в живом организме. После гибели организм не в состоянии поглощать угле-
род и соотношение между
12
C и
14
C изменяется. По меняющемуся соотношению
между
12
C и
14
C можно относительно точно определить возраст мертвого орга-
низма. Метод достаточно чувствителен, если возраст не превышает 5
⋅ 10
4
лет.

22
Глава 2. Радиоактивность
Атомными часами для определения возраста Земли служит
238
U (T
= 4,56 ⋅ 10
9
лет)
и
232
Th (T
= 14 ⋅ 10
9
лет). Конечным продуктом их распада являются изотопы
свинца
206
Pb и
208
Pb. (Изначальный изотоп
204
Pb.) Если предположить, что весь
радиогенный свинец образуется как продукт распада, то можно вычислить возраст
Земли. Надо точно измерить количество различных изотопов Pb, содержащихся,
например, в радий-урановых рудах. Этот метод дает примерно 4,5
⋅ 10
9
лет, что
хорошо согласуется с другими методами определения возраста Земли.
. . . . . . . . . . . . . . . . . . . . . .
Пример 2.2
. . . . . . . . . . . . . . . . . . . . .
В урановых рудах содержится примесь чистого свинца
206
Pb. Предполагая,
что весь свинец получился в результате распада
238
U, определить возраст урано-
вой руды. В 1 г урана содержится 0,3 г
206
Pb.
Решение:
Найдем начальное число ядер урана:
N
0
=
m
u
µ
u
⋅ N
A
=
1
⋅ 6,02 ⋅ 10
23
238
= 2,53 ⋅ 10
21
(ядер).
Аналогично — число ядер Pb:
N
(Pb)
=
m
Pb
µ
Pb
N
A
=
0,3
⋅ 6,02 ⋅ 10
23
206
= 8,77 ⋅ 10
20
(ядер).
N
Pb
= N — числу распавшихся ядер урана.
N
= N
0
(1 − e
−
ln 2
T
t
) = N
0
− N
0
e
−
ln 2
T
t
;
ln
(N
0
− N) = ln N
0
−
ln 2
T
t,
⇒ t =
ln
(
N
0
N
0
− N
) ⋅ T
ln 2
=
=
ln
[
2,53
⋅ 10
21
(2,53 − 0,877) ⋅ 10
21
] ⋅ 4,56 ⋅ 10
9
ln 2
= 2,8 ⋅ 10
9
(лeт).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 Активность
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Активность (А) — число распадов в единицу времени.
A
= ∣
dN
p
dt
∣ = λ ⋅ N.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2.4 Виды распадов ядер
23
Напомним:
λ — вероятность распада одного ядра за 1 с.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Поскольку в процессе распада исходное число ядер уменьшается,
то уменьшается и активность образца. Найдем закон изменения
активности:
N
p
= N
0
− N
0
⋅ e
−λt
;
dN
p
dt
= N
0
⋅ λ ⋅ e
−λt
.
Если A
0
= N
0
⋅ λ — начальная активность, то
A
= A
0
⋅ e
−λt
.
(2.1)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
В СИ единицей измерения активности является Бк (беккерель) — 1 распад за
1 c. Старые единицы активности: 1 Ku (кюри) = 3,7
⋅ 10
10
Бк; 1 Pd (резерфорд) =
= 10
6
Бк. (1 Ku имеет активность 1 г чистого радия.)
2.4 Виды распадов ядер
2.4.1
α-распад
Еще в 1909 г. Э. Резерфорд доказал, что
α-частицы — дважды ионизированные
атомы гелия:
4
2
α ≡
4
2
He. Распад протекает по схеме
A
Z
X
→
A
−4
Z
−2
Y
+
4
2
α,
α-распад обычно сопровождается испусканием дочерним ядром γ-фотона.
Пример реального
α-распада:
238
92
U
→
234
90
Th
+
4
2
α.
Скорости вылетевших
α-частиц ∼ 10
7
м
/c. Пролетая через вещество, α-частица
постепенно теряет свою энергию, затрачивая ее на ионизацию молекул вещества.
Энергия
α-частицы ≅ 3–10 МэВ, на образование одной пары ионов в воздухе тра-
тится
∼ 35 эВ, поэтому α-частица может ионизировать ∼ 10
5
молекул. Чем больше
плотность вещества, тем меньше длина свободного пробега. В твердом веществе
пробег
α-частиц ∼ 10–2 мкм, т. е. задерживается металлической фольгой толщиной
в лист бумаги.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Кинетическая энергия
α-частиц возникает за счет избытка энергии
покоя материнского ядра над суммарной энергией покоя дочернего
ядра и
α-частицы. Полная энергия, выделяющаяся при α-распаде:
Q
= E
cв
(A − 4, Z − 2) + E
cв
(α) − E
cв
(Z, A).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
Глава 2. Радиоактивность
Эта энергия распределяется между дочерним ядром и
α-частицей обратно про-
порционально их массам.
α-распад возможен, если Q > 0, а для этого необходимо, чтобы E
cв
материнско-
го ядра E
cв
(Z, A) была меньше суммы энергий связи дочернего ядра и
α-частицы,
т. е. удельная энергия связи в дочернем ядре должна быть больше, чем в материн-
ском. Следовательно,
α-распаду подвержены только тяжелые ядра (A > 200).
В большинстве случаев радиоактивное вещество испускает несколько групп
близкой, но различной энергии. Это обусловлено тем, что дочернее ядро может
возникать не только в нормальном, но и в возбужденном состояниях. Среднее вре-
мя жизни ядра в возбужденном состоянии для большинства ядер
τ ≅ 10
−8
–10
−15
c.
За время
τ дочернее ядро переходит в нормальное состояние, испуская γ-фотон.
Энергия возбужденного дочернего ядра может быть выделена и другим способом:
возбужденное ядро может испустить какую-либо частицу (p, n, e
−
).
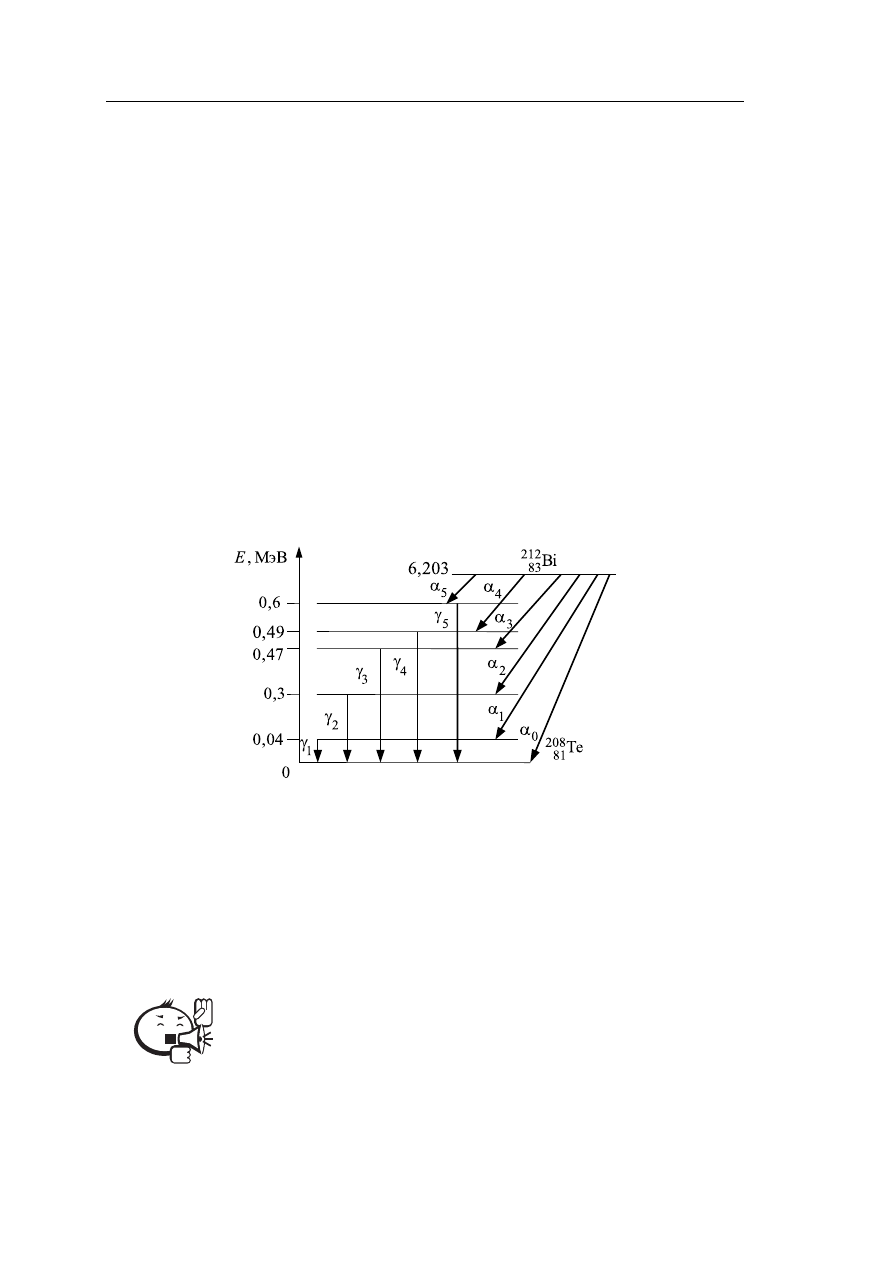
Рисунок 2.2 иллюстрирует на примере распада
212
Bi энергетическую структуру
как
α-частиц, так и образующихся при этом γ-фотонов. Реакция распада:
212
83
Bi
→
208
81
Te
+
4
2
α +
0
0
γ.
Рис. 2.2 – Тонкая структура
α-спектра при распаде ядер
212
Bi
Ясно, что если
α-частица будет иметь энергию 6,203 МэВ, то γ-частица при
этом не возникнет [1].
Теорию
α-распада создали независимо друг от друга Г. Гамов и Р. Герни
с Э. Кондоном (1928 г). Потенциальный барьер, который нужно преодолеть
α-частице, чтобы покинуть ядро, ≅ 25–30 МэВ. Однако максимальная кинетиче-
ская энергия
α-частиц, вылетающих из различных ядер, не превышает E ≅ 10 Mэв.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Этот парадокс не могли объяснить до тех пор, пока не применили
представление о туннельном эффекте.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
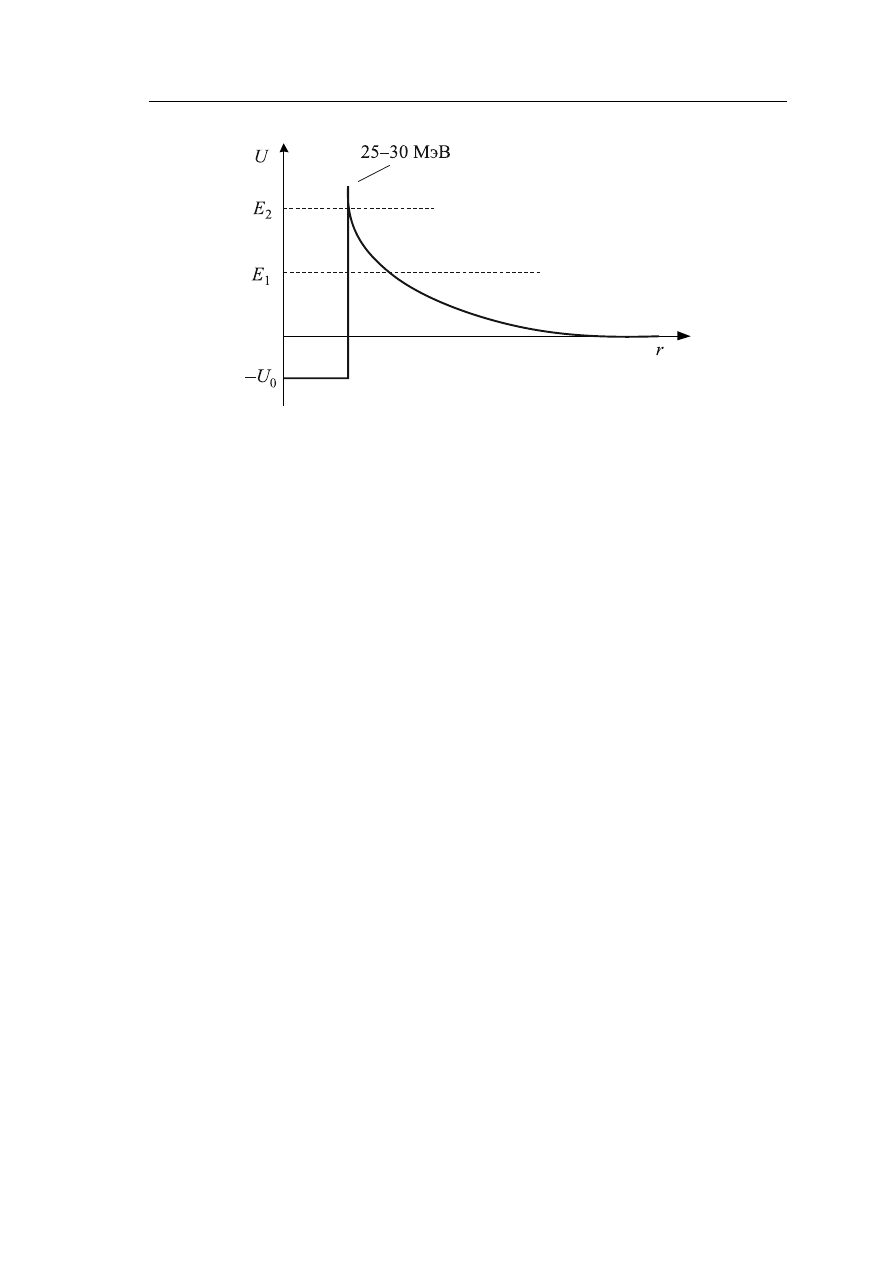
Как и любая частица материи,
α-частица, обладая волновыми свойствами и на-
ходясь в потенциальной яме (рис. 2.3), может принимать только дискретные зна-
чения энергии: E
1
, E
2
и т. д.
2.4 Виды распадов ядер
25
Рис. 2.3 – К объяснению туннельного просачивания
α-частиц
Понятно, что вылетающие из ядра
α-частицы будут иметь те же дискретные
значения энергии. Поскольку вероятность просачивания сквозь барьер экспоненци-
ально зависит от ширины барьера, стала понятной и сильная зависимость времени
жизни радиоактивного ядра от значения энергии
α-частицы: для
238
U E
α
= 4,2 МэВ
и период полураспада T
= 4,5 ⋅ 10
9
лет; для
226
Ra E
α
= 4,8 МэВ, T = 1,6 ⋅ 10
3
лет;
для
222
Rn E
α
= 5,5 МэВ и T = 3,8 сут; для
218
Po E
α
= 6,0 МэВ, T = 3 мин; для
214
Po E
α
= 7,07 МэВ и T = 1,6 ⋅ 10
−4
с [2, 4].
2.4.2
β-распад ядер
Существуют три вида
β-распада: электронный (β
−
-распад), позитронный
(
β
+
-распад), электронный захват (K-захват).
Электронный
β
−
-распад протекает по схеме
A
Z
x
→
A
Z
+1
y
+
0
−1
e
+ ˜v
e
,
где ˜v
e
— электронное антинейтрино (см. ниже).
Весь процесс протекает так, как если бы один из нейтронов превратился в протон:
1
0
n
→
1
1
p
+
0
−1
e
+ ˜v
e
.
Так как нейтроны есть у всех ядер, то
β-активные ядра более многочисленны:
у всех элементов есть изотопы, обладающие
β
−
-активностью. Примером
β
−
-распа-
да может служить превращение тория (Th) в протактиний (Pa):
234
90
Th
→
234
91
Pa
+
0
−1
e
+ ˜v
e
.
Не сразу стало ясно, что все происходит именно так. В отличие от
α-распада,
где
α-частицы обладают строго определенными значениями энергий, электроны
обладают самой разной кинетической энергией, от 0 до E
max
(рис. 2.4).
E
max
соответствует разности между энергией покоя ядра и суммой энергий по-
коя дочернего ядра и электрона. Но почему вылетают электроны с E
< E
max
? Не
выполняется закон сохранения энергии в этом процессе? Н. Бор допускал эту воз-
можность. В 1932 г. В. Паули (1900 –1958 гг.) высказал мысль, что при
β-распаде
вместе с электроном вылетает еще одна частица, которая и уносит энергию, рав-
ную разности между E
max
и энергией вылетевшего электрона.