ВУЗ: Алтайский Государственный Университет
Категория: Учебное пособие
Дисциплина: Аналитические методы в экономике
Добавлен: 23.10.2018
Просмотров: 2169
Скачиваний: 12
Тема 1.3. Организация и обработка данных экспертного опроса
Метод экспертных оценок является одним из эффективных инструментов аналитических исследований и характеризуется применением количественных оценок при обработке экспертной информации5. Он включает в себя три составляющие6:
1. Интуитивно-логический анализ задачи. Строится на логическом мышлении и интуиции экспертов, технологии основаны на их знании и опыте. Этим объясняется высокий уровень требований, предъявляемых к экспертам.
2. Решение и выдача экспертных оценок. Эта процедура представляет собой завершающую часть работы эксперта. Им формируется решение по рассматриваемой проблеме и дается оценка ожидаемых результатов.
3. Обработка результатов решения. Полученные от экспертов оценки должны быть обработаны с целью получения итоговой оценки проблемы. В зависимости от поставленной задачи изменяется количество выполняемых на этом этапе расчетных и логических процедур. Для обеспечения оперативности и минимизации ошибок на данном этапе целесообразно использование вычислительной техники.
Ниже рассмотрим одну из задач, решаемых с использованием экспертного метода аналитических исследований – задачу ранжирования альтернатив.
Используемые количественные методы существенно зависят от выбранной шкалы измерения признакового пространства рассматриваемой проблемы и поставленной задачи обработки данных. При выборе одной из нескольких альтернатив рекомендуется использовать порядковую шкалу и поставить перед экспертами задачу ранжирования списка альтернатив (объектов). Рассмотрим эти понятия.
Порядковая шкала. Цель состоит в упорядочении объектов (явлений), а точнее, в выявлении с помощью экспертов скрытой упорядоченности, которая, по предположению, присуща множеству объектов. Результатом оценки является решение о том, что какой-либо объект (явление) предпочтительнее другого в отношении какого-то критерия.
Ранжирование – это расположение
объектов в порядке возрастания или
убывания какого-либо присущего им
свойства7.
Ранжирование позволяет выбрать из
исследуемой совокупности факторов
наиболее существенный. Результатом
проведения ранжирования является
ранжировка. Если имеется
 объектов,
то в результате их ранжирования i-ым
экспертом каждый объект получает оценку
объектов,
то в результате их ранжирования i-ым
экспертом каждый объект получает оценку
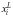 – ранг, приписываемый L-му
объекту i-ым экспертом.
Значения
– ранг, приписываемый L-му
объекту i-ым экспертом.
Значения
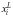 находятся
в интервале от 1 до
находятся
в интервале от 1 до
 .
Ранг самого важного фактора равен
единице, наименее значимого – числу
.
Ранг самого важного фактора равен
единице, наименее значимого – числу
 .
Ранжировкой i-го эксперта
называется последовательность рангов
.
Ранжировкой i-го эксперта
называется последовательность рангов
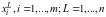 ,
где
,
где
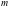 -
число привлеченных экспертов.
-
число привлеченных экспертов.
Рассмотрим технологию ранжирования. Применительно к ранжированию рассмотрим методику обработки экспертной информации. Она включает три этапа:
-
Сбор экспертной информации.
-
Оценка компетенции экспертов и определение их веса.
-
Ранжирование альтернатив.
-
Проверка согласованности мнений экспертов.
На первом этапе формируется таблица
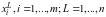 .
На втором этапе вычисляются коэффициенты
компетенции экспертов
.
На втором этапе вычисляются коэффициенты
компетенции экспертов
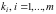 ,
значение которых неотрицательно и в
сумме равно единице. Информацией для
их вычисления могут служить суждения
экспертов о степени компетенции друг
друга. Для ранжирования альтернатив
используются средневзвешенные оценки.
,
значение которых неотрицательно и в
сумме равно единице. Информацией для
их вычисления могут служить суждения
экспертов о степени компетенции друг
друга. Для ранжирования альтернатив
используются средневзвешенные оценки.
Проверку согласованности мнений экспертов рекомендуется в литературе проводить с использованием коэффициента конкордации по Кэнделу и сравнением его значения с табличным для выбранного уровня значимости. В работе, приведенной в сноске 5 на с. 203-204, приведены табличные данные для указанного сравнения при 0,05 (5%) и 0,01 (1%) уровней значимости. Последняя операция необходима для решения вопроса о принятии для практики решения, выбранного экспертами или о продолжении процедуры экспертного анализа, в том числе и от отказа в использовании данного метода.
Приведем результаты сравнения 5 альтернатив 8 экспертами в нашем случае. Рассматривалась оценки рангов 5 сценарных оценок ВВП России на текущий год:
-
-1% и менее.
-
(-1% – 0%].
-
(0% – 1%].
-
(1% – 2%).
-
2% и более.
Задание 1.1. Сформировать экспертную группу, организовать сбор данных и провести обработку экспертной информации с использованием MS Excel (программа в файле «ЭКСПЕРТНЫЙ-опрос-ПРИМЕР.xls прилагаемого программного обеспечения дисциплины).
Раздел 2. Моделирование процессов и процедур принятия решений, примеры.
Моделирование процессов и оптимальных решений. Многокритериальные модели принятия решений. Производственные функции. Задача оптимального среднесрочного планирования. Типовые задачи, решаемые с использованием инструмента Excel «Поиск решения».

Тема 2.1. Моделирование процессов и оптимальных решений. Многокритериальные модели принятия решений
2.1.1. Основные определения
В теории экономико-математического моделирования выделяют 2 основных класса математических моделей (модели процессов и модели решений), используемых в трех типах исследовательских задач:
-
оценка параметров экономических процессов и систем;
-
прогнозирование временных рядов и событий;
-
обоснование оптимальных решений.
Эти задачи можно выразить формулой активных (целенаправленных) действий: «знать», «предвидеть», «управлять». Отмеченная классификация математических моделей представлена на рисунке 2.1.1.

Полезно пользоваться определением математических (компьютерных) моделей. ММ это отражение в математических символах или в компьютерных операторах существенных сторон исследуемого явления или процесса.
Существует строгое различие математических и компьютерных моделей. Свойства математических моделей и получаемые с их использованием результатов исследуются строгим математическим аппаратом (методами). Компьютерные модели исследуются на ЭВМ.
2.1.2. Моделирование процессов
Структурно модели процессов представляют в виде «черного ящика» (рисунок 2.1).
Задача математического моделирования процессов при условии достаточно точных наблюдений за входными переменными и выходной переменной формулируется следующим образом:
Найти функцию
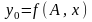 и доверительный интервал
и доверительный интервал
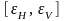 для
значений
для
значений
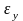 .(2.1)
.(2.1)
Тогда
на практике можно знать ожидаемые
значения выходной переменной при
известных значениях вектора
 :
:
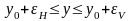 .
.
Математическая модель (2.1) называется эмпирической (ЭМП), если основная информация для ее построения – результаты наблюдений моделируемого процесса или наблюдений за процессами – аналогами моделируемого, и теоретической (ТМП), если существенно используются знания соответствующей теории.
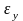
…
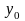
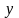
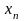
2.1.3. Моделирование решений
В данном месте следует пояснить объект моделирования, учитывая, что модель – отражение реальности. Конечным результатом модельных расчетов, является вариант решения, который предлагает аналитик. Но аналитик не несет ответственности за последствия принимаемого решения (кроме особых процедур страхования профессиональной ответственности). Кроме того, заказчик может дать задание аналитику предсказать решение конкурента в конкретной экономической ситуации.
В теории экономико-математического моделирования принято считать объектом моделирования лицо, принимающее решение (ЛПР). ЛПР – обобщенное и абстрактное понятие, в которое включено совокупность свойств реальных центров принятия решений, условий (экономических, финансовых, информационных, временных) в которых это решение формируется, границы зон ответственности решений, возможности (или невозможности) их корректирования и т.д. Реально решения могут приниматься с разной степенью рациональности в стандартных или в уникальных ситуациях.
В экономической литературе наиболее простым и часто используемым образом ЛПР выступает экономический человек8. Этим свойством наделяют субъектов экономической деятельности: не только отдельных людей, но и руководство предприятий, корпораций, органов государственного, местного самоуправления и стран в целом.
В
простом случае считается, что ЛПР знает
список возможных решений (математически
множество
 ),
полезность каждого решения (математически
функция
),
полезность каждого решения (математически
функция
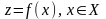 )
и выбирает оптимальное решение
)
и выбирает оптимальное решение
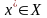 ,
которое имеет максимальную полезность.
,
которое имеет максимальную полезность.
Математически
модель решений (1 ЛПР) записывается так:
найти
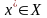 из условий9:
из условий9:
 . (2.2)
. (2.2)
В этом выражении
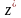 или
или
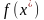 – значение оптимальной (максимальной)
полезности.
– значение оптимальной (максимальной)
полезности.
В настоящее время разработаны варианты математических моделей решений (1 ЛПР) в условиях ограниченной информированности (ЛПР не знает полного списка решений, ЛПР неточно оценивает полезности решений, информированность аналитика не совпадает с информированностью ЛПР). Основные подходы к построению таких моделей связаны с использованием теории вероятности (модели решений в условиях риска) и интервального (теоретико множественного) анализа (модели решений в условиях неопределенности).
2.1.4. Моделирование решений. Теория игр
На
рисунке 2.2.1 выделены математические
модели решений с n ЛПР
(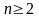 ),
которые используются для исследования
экономических систем с многими центрами
принятия решений. На практике трудно
разделить системы с одним и многими
центрами принятия решений. Но характерными
примерами систем с n ЛПР
выступают системы: «работник-работодатель»,
«контрольный орган-исполнитель»,
«товарный или финансовый рынки в условиях
конкуренции», «корпоративное управление»10.
),
которые используются для исследования
экономических систем с многими центрами
принятия решений. На практике трудно
разделить системы с одним и многими
центрами принятия решений. Но характерными
примерами систем с n ЛПР
выступают системы: «работник-работодатель»,
«контрольный орган-исполнитель»,
«товарный или финансовый рынки в условиях
конкуренции», «корпоративное управление»10.
Задачей аналитика при исследовании этих систем выступает построение математической (компьютерной) модели, с использованием которой можно предсказать решения всех ЛПР. Классической работой в данной области является книга Дж. фон Нейман, О. Моргенштерн, которая написана в США в 1944 г. На русском языке книга стала известной с 1970 г.11
Основные принципы математического моделирования экономических процессов и систем сохраняются и в рассматриваемой области. Дополнительными задачами выступают обоснование знаний всех ЛПР объекта моделирования о своих списках решений, целевых функциях, порядках ходов, об уровнях взаимной информированности и принятых правилах совестного выбора и реализации решений. Трудности математического моделирования связаны с наличием неполной информации об условиях выбора решений и о решениях, принимаемых другими ЛПР12.
2.1.5. Моделирование решений. Многокритериальные модели принятия решений
Рассматриваем
модели решений с одним ЛПР, которое
оценивает полезность решений вектором
показателей. Например эффект инвестиций
определяется их доходностью и уровнем
риска. При выборе варианта решения
необходимо найти компромисс между этими
критериями. В общем случае на множестве
решений
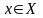 могут быть заданы n
(
могут быть заданы n
(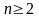 )
целевых показателей, часть которых
требуется минимизировать, а часть –
максимизировать. Без потери общности
можно считать, что все критерии следует
максимизировать13.
В теории экономико-математического
моделирования используют 2 подхода:
)
целевых показателей, часть которых
требуется минимизировать, а часть –
максимизировать. Без потери общности
можно считать, что все критерии следует
максимизировать13.
В теории экономико-математического
моделирования используют 2 подхода:
1. Свертка критериев, т.е. сведение многокритериальной задачи к однокритериальной задаче обоснования решений. Используют линейную и специальные нелинейные функции свертки частных критериев.
2. Выбор одного критерия в качестве ведущего и введение ограничения на уровни снижения значений по всем другим критериям.
Пример
2.1. Пусть задана задача принятия
решений с n (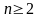 )
критериями
)
критериями
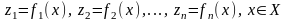 .
Введем интегральный критерий
.
Введем интегральный критерий
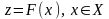 :
:
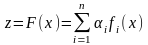 ,
где
,
где
 – «веса» частных критериев. Тогда
многокритериальная модель решения
сводится к модели (2.2) с целевой функцией
– «веса» частных критериев. Тогда
многокритериальная модель решения
сводится к модели (2.2) с целевой функцией
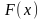 .
.
Задание 2.1. Ниже в разделе 3 приведена модель Марковица для поиска оптимального инвестиционного портфеля. Показать, что данная модель является двухкритериальной, а для поиска решения выбран подход 2, т.е. выбран ведущий критерий (какой?), а второй критерий (какой?) ограничен по значению.
Тема 2.2. Производственные функции
Производственная функция (также функция производства) — экономико-математическая количественная зависимость между величинами выпуска (количество продукции) и факторами производства, такими как затраты ресурсов, уровень технологий14.
Производственная функция является примером моделей процессов (часто это теоретическая модель процесса производства товаров и/или услуг). Рассматривается годовое количество произведенной фирмой продукции в стоимостной или натуральной форме. Факторами производства выступают объемы потребленных фирмой ресурсов (в стоимостном или в натуральном измерении). Главными ресурсами выступают потребленные за год количества труда и капитала15.
Определение.
Функция
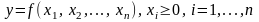 называется производственной, если
выполнены следующие ее свойства:
называется производственной, если
выполнены следующие ее свойства:
1. Нулевой выпуск в отсутствии одного или нескольких ресурсов.
2.
Неотрицательная производительность
факторов
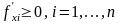 .
.
3.
Убывающая эффективность факторов
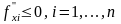 .
.
4.
Линейная однородность или постоянная
отдача от масштаба
 .
.
Примеры производственных функций:
1.
Классическая производственная функция
Кобба-Дугласа (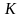 – амортизация капитала фирмы,
– амортизация капитала фирмы,
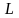 – фонд заработной платы за рассматриваемый
период времени):
– фонд заработной платы за рассматриваемый
период времени):
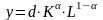 , (2.4)
, (2.4)
где
 – параметры функции, индивидуальные
для фирмы (
– параметры функции, индивидуальные
для фирмы (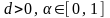 ).
).
2. Обобщенная функция Кобба-Дугласа:
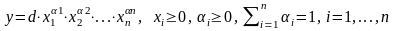 . (2.5)
. (2.5)
3. Линейная производственная функция:
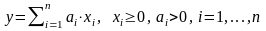 . (2.6)
. (2.6)
4. Производственная функция с нулевой эластичностью замещения ресурсов:
 . (2.7)
. (2.7)
Задание 2.2. В записанных функциях укажите аргументы и параметры, поясните их экономический смысл и размерности.
Задание 2.3. Покажите, что функции (2.4) – (2.7) удовлетворяют определению производственных функций.
Тема 2.3. Задача оптимального среднесрочного плана развития производства
С использованием производственной функции рассмотрим задачу выбора оптимального соотношения запасов ресурсов. Эту задачу можно интерпретировать как задачу среднесрочного планирования развития фирмы.
Пусть
для некоторой фирмы известна
производственная функция, ее товарная
и ресурсная и технологическая политика
стабильна, а спрос на продукцию
неограничен. Пусть также в среднесрочной
перспективе заданы интервалы
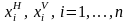 возможного изменения каждого из
существенных производственных ресурсов:
возможного изменения каждого из
существенных производственных ресурсов:
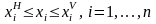 .
Тогда можно найти оптимальные значения
ресурсного обеспечения производства
решение следующей задачи. Найти
.
Тогда можно найти оптимальные значения
ресурсного обеспечения производства
решение следующей задачи. Найти
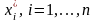 из условий:
из условий: