В приведенной таблице первые три портфеля совпадают по всем параметрам, так как при выбранных исходных данных ограничение (3.6) модели Марковица выполняется как строгое неравенство. По остальным портфелям наблюдается закономерность в изменении долей активов А1 – А5, включенных в портфель (см. данные столбцов 2 – 6 таблицы). Характерным свойством таблицы вариантов является увеличение риска доходности, определяемого величиной доверительного интервала (столбец ДИ%), с ростом средней доходности (столбец данных СД%).

Задача аналитика состоит в обосновании рекомендации для инвестора по выбору оптимального варианта портфеля. Данная задача может быть решена с использованием экономико-математических методов принятия решений в условиях риска и неопределенности¹⁹.

При использовании максиминных стратегий (принцип максимальной гарантированной доходности портфеля) оптимальным вариантом в таблице 3.1 следует считать портфель 7.

Задание 3.3. Пояснить порядок выбора варианта 7 и дать его полную характеристику.

Задание 3.4. Обосновать порядок проведения дополнительных расчетов при необходимости повышения точности расчетов оптимального портфеля.

Тема 3.3. Поддержка решений при оптимизации портфельных инвестиций в условиях стабильной и нестабильной экономики

Проведенный выше портфельный анализ базировался на использовании теоретических знаниях²⁰ и в модели Марковица использованы теоретические модели процессов. Однако в настоящее время не существует теории для оценок параметров этой модели: ковариационной матрицы 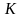в формуле (3.4) и прогнозов 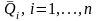средних доходностей выбранных активов в формуле (3.3). На практике эти количественные данные оцениваются на основе эмпирического подхода (на основе наблюдений количественных данных).

Следует иметь в виду, что основной принцип эмпирического подхода «так было, так будет!» не всегда выполняется²¹. Эмпирические знания верны для стабильной экономики, для которой комплекс закономерностей формирования событий в прошлом без изменения может быть перенесен на будущее. Тогда для оценок 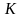и 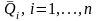можно использовать временные ряды совместных значений доходностей в прошлом и статистические методы их обработки. Пример исходных данных квартальных доходностей 5 активов представлен в таблице 3.2.

Таблица 3.2. Квартальные наблюдения процентных ставок по финансовым инструментам

№ квартала	1	2	3	4	5
1	2,5%	-1,4%	2,2%	2,3%	-2,6%
2	2,9%	4,9%	6,8%	4,8%	3,8%
3	2,4%	1,6%	4,9%	3,7%	0,1%
4	1,8%	2,5%	4,0%	3,4%	0,6%
5	2,2%	4,7%	6,1%	4,8%	2,5%
6	3,5%	4,7%	7,0%	5,5%	6,6%
7	3,3%	-0,4%	2,9%	3,2%	-1,6%
8	2,1%	2,9%	5,5%	4,1%	1,9%
9	1,8%	3,3%	5,9%	4,2%	1,6%
10	2,0%	0,1%	3,3%	3,2%	0,3%
11	3,0%	4,9%	6,8%	5,2%	4,5%
12	2,6%	4,2%	5,8%	4,9%	4,4%
Сред	2,51%	2,67%	5,10%	4,11%	1,84%

---

На основе этих исходных данных в условиях стабильной экономики можно оценить требуемые параметры. Средние доходности активов приведены в последней строке таблицы 3.2, а ковариационная матрица, вычисленная с использованием встроенной функции КАВАР() приведена в таблице 3.3.

Эмпирический подход для оценки параметров модели Марковица может быть использован в условиях нестабильной экономики, т.е. экономики, для которой в будущем сохраняются тенденции изменений экономических показателей. Тогда для поиска данных, аналогичных таблицам 3.2 и 3.3 применяют эконометрические методы анализа временных рядов.

Таблица 3.3. Оценки ковариационной матрицы 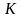формулы (3.4) по данным таблицы 3.2.

i\j	1	2	3	4	5
1	2,925E-05	1,667E-05	1,948E-05	1,877E-05	5,062E-05
2	1,667E-05	0,000456	0,000323	0,000188	0,000498
3	1,948E-05	0,000323	0,000245	0,000139	0,000368
4	1,877E-05	0,000188	0,000139	0,000086	0,000229
5	5,062E-05	0,000498	0,000368	0,000229	0,000659

Состояние экономики, для которой принципы эмпирического моделирования процессов неприменимы, называется кризисной. Профессиональные знания и опыт аналитика направлены на надежную оценку состояния экономики при решении конкретной аналитической задачи²².

Методические подходы портфельного анализа в среде Excel с использованием инструмента «Поиск решения» в условиях стабильной и нестабильной экономик приведены в описании соответствующих лабораторных работ.

---

Раздел 4. Математические и инструментальные методы поддержки принятия решений при стимулировании менеджеров финансовых организаций

Модель поведения работника на рабочем месте. Модель оптимизации бонуса менеджеров финансовых организаций. Расчетные работы: «Активность работников»; «Оптимизация бонуса»

Тема 4.1. Модель поведения работника на рабочем месте

В данном разделе рассматривается для экономического человека зависимость объема продаж труда, т.е. фактической трудовой активности (ФТА) от его цены (р) на локальном рынке труда и при условии, что «поле деятельности» – объем оплачиваемой работы – не ограничен. Изучаем среднедневную активность работника, т.е. рассматриваем трудовые процессы в среднем за рабочий день.

Приведем основные определения. Справедливой (рыночно равновесной) будем считать сделку, при которой согласованная заработная плата равна произведению количества продаваемого труда на его цену.

В качестве меры труда (единицы измерения объема работы) выберем часовую норму труда (ЧНТ) – объем работы, который реально выполняет среднерыночный (для сегмента локального рынка) работник в течение одного рабочего часа. Эта характеристика для среднерыночного работника может быть оценена как часовая норма выработки. Такой работник за 8-часовой рабочий день выполнит объем работы 8 ЧНТ. При оплате труда в 100 руб. за ЧНТ его месячная заработная плата (20 рабочих дней) равна 16 000 руб.

Потенциал трудовой активности (ПТА) работника определим, как объем работы в ЧНТ, который он способен выполнить в среднем за рабочий день. Мы также используем понятие фактическая трудовая активность (ФТА) работника.

С читаем, что ФТА меняется в пределах [0, ПТА]. Оплата единицы труда р в рублях за ЧНТ также меняется. Так на рисунке 4.1 она меняется от 0 до 72 руб. за ЧНТ.

---

Для построения графика можно задать его характерные точки: p_min – минимальная ставка ЧНТ, которая начинает интересовать рабочего; А(ФТА_н, р_н) – промежуточная точка «привязки графика» по данным локального рынка труда.

Приведем пример аналитического выражения зависимости на рисунка 4.4:

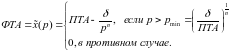(4.1)

Приведенный рисунок показывает, что при 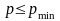функция 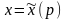принимает нулевые значения. Точка 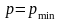найдена решением уравнения 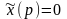. При функция 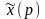выпукла (вверх), монотонно возрастает и при больших значениях сколь угодно близко приближается к значению ПТА. Перечисленные свойства качественно соответствуют закономерностям поведения работников при стимулировании интенсивности их труда.

Мы считаем возможным построение конкретной функции для среднерыночного и индивидуального работника на основе дополнительной информации, которую участники трудовых отношений могут получить анализом условий локального рынка труда.

Введем для локальных рынков интегральный показатель интенсивности труда (обозначим его через 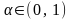, как отношение среднерыночной активности работников к ПТА. Предположим, что значение этого показателя постоянно для выделенной профессиональной группы при среднерыночных условиях оплаты труда и не зависит от квалификации, возраста работников и других индивидуальных характеристик.

Тогда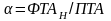 определяется нами как фундаментальная характеристика локального рынка труда для всех работников выделенного сегмента. Для среднерыночного работника параметры функции (4.1) имеют вид (получены решением уравнения ):

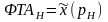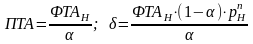. (4.2)

Рассмотрим индивидуального работника, который отличается, по нашему мнению, от среднерыночного на рассматриваемом сегменте локального рынка труда по квалификации (индекс 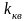), интенсивности труда (индекс 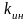) и по уровню отношения к денежному вознаграждению (индекс валентности – v). Считаем, что значения введенных индексов для среднерыночного работника равны единице. Индекс квалификации мы определяем отношением объемов выполненной работы индивидуального и среднерыночного работников при одинаковой интенсивности за одно и тоже рабочее время. Индекс интенсивности труда – это отношение производительности при одинаковых квалификациях сравниваемых работников.

Тогда фактический объем работы, который выполнит индивидуальный работник за рабочий день при среднерыночных условиях оплаты труда (при v = 1), определится по формуле:

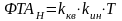, (4.3)

где T – средняя продолжительность рабочего дня в рабочих часах.

Рассмотрим фактор валентности. Можно показать, что уровень активности 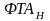достигается для работника с индексом мотивации (валентности) v при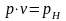 . Тогда точка А на рисунке 4.1 имеет координаты: .

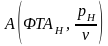Окончательно в функции (4.1) поведения всех работников выделенного сектора локального рынка труда параметры имеют следующие выражения:

---

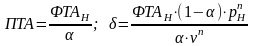. (4.4)

Объем работы в ЧНТ, который фактически выполнит работник в среднем за рабочий день, вычисляется по формуле (4.1) с учетом формул (4.3), (4.4) и заданных значениях 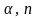. При расчетах рекомендуется использовать следующие значения характеристик работников: ²³.

Тема 4.2. Модель оптимизации бонуса менеджеров финансовых организаций

Эффективным механизмом стимулирования исполнительной структуры является выделение доли 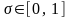, полученной этой структурой прибыли в качестве бонуса (премиального вознаграждения). Тогда оптимальное значение 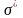должно обеспечивать максимальные результаты для собственника рассматриваемой экономической системы.

В качестве примера рассмотрим задачу оптимизации бонуса исполнительному директору фирмы, зависимость среднедневного объема работ которого от ставки оплаты труда 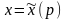задана выражением (4.1).

Рассмотрим математическую модель обоснования оптимального решения собственников фирмы по стимулированию исполнительной дирекции. Обозначим через

(4.5)

зависимость среднедневной валовой прибыли фирмы, полученной за счет активности стимулируемых менеджеров.

Функцию (4.5) дополнительной прибыли от трудового вклада менеджеров можно получить на основе функции Кобба-Дугласа при постоянной величине капитала фирмы.

Дополнительная валовая прибыль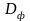 разделяется на чистую прибыль собственника 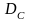и оплату труда менеджеров :

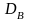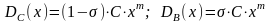(4.6)

С учетом выражения (4.6) задачу выбора оптимального значения 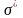запишем в следующем виде. Найти 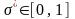при котором доход собственника является максимальным:

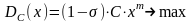. (4.7)

Можно показать, что при фиксированной величине 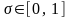и заданной активности 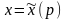оплата 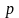единицы активности и уровень активности 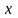определятся из следующего уравнения:

, (4.8)

решение которого необходимо учитывать как дополнительное условие задачи (4.7).

В описании к лабораторной работе 4 представлена методика идентификации функции (4.5) и программное обеспечение в среде Excel для решения задачи (4.7) в случае, когда в (4.1) параметр n равен единице.

Тема 4.3. Расчетные работы: «Активность работников»; «Оптимизация бонуса»

Приведенные в данном разделе аналитические задания и порядок их выполнения изложены в описаниях к лабораторным работам²⁴.

Задача 4.3.1. Моделирование активности персонала фирмы

С использованием математической модели активности работника (4.1) провести расчеты зависимости активности от оплаты единицы объема работ.

Используя полученную зависимость провести расчеты:

А) Среднедневной активности (ФТА) при оплате 1 ЧНТ равной 80 рублей.

Б) Требуемую оплату 1 ЧНТ для выполнения работником 13 ЧНТ в среднем за рабочий день.

В) Рассчитать уровни заработной платы работника в среднем за рабочий день и месяц по данным пп. А) и Б) (принять 20 рабочих дней в месяц).

Расчеты выполнить с использованием программы в среде MS Excel (файл «Активность работника.xls»). Исходные данные приведены в таблицах 4.1, 4.2, 4.3. Результаты представлены таблицей 4.4. и рисунком 4.1.

---

Смотрите также файлы

• Шаблон оформления ТЗ.pdf

• Управление проектами разработки ПО (теория).pdf

• Управление проектами разработки ПО (СРС).pdf

• Управление программами и проектами.pdf

• Разработка календарного плана-графика.pdf