ВУЗ: Алтайский Государственный Университет
Категория: Учебное пособие
Дисциплина: Аналитические методы в экономике
Добавлен: 23.10.2018
Просмотров: 2170
Скачиваний: 12
Таблица 4.1. Характеристика оборудования рабочего места
|
№ п/п |
Показатели |
Обозначение |
Значение |
|
1 |
Предельная производительность, ЧНТ/час |
ЧПТАоб |
1,5 |
|
2 |
Период времени использования, час/сутки |
Тоб |
24 |
|
3 |
Коэффициент использования оборудования, % |
КИоб |
100,0% |
Таблица 4.2. Трудовая характеристика сотрудника
|
№ п/п |
Показатели |
Обозначение |
Значение |
|
1 |
Продолжительность рабочего дня, час |
Тр |
9,00 |
|
2 |
Коэффициент интенсивности труда |
Кит |
1,10 |
|
3 |
Коэффициент квалификации |
Ккв |
1,20 |
|
4 |
Валентность работника |
Вр |
1,20 |
Таблица 4.3. Характеристика локального рынка труда
|
№ п/п |
Показатели для данной профессии |
Обозначение |
Значение |
|
1 |
Средний коэффициент интенсивности труда |
Альфа |
0,70 |
|
2 |
Среднемесячная заработная плата, руб. |
ЗПн |
10000,00 |
|
3 |
Среднемесячное число рабочих часов, час |
Тмес |
170,00 |
Таблица 4.4. Расчетные показатели трудового процесса
|
№ п/п |
Наименование показателей |
Обозначения |
Значение |
|
1 |
Потенциал трудовой активности работника |
ПТАр |
16,97 |
|
2 |
Сменная производительность оборудования |
ПТАоб |
36,00 |
|
3 |
Потенциал трудовой активности рабочего места |
ПТА |
16,97 |
|
4 |
Расценка среднерыночная, руб/ЧНТ |
Рн |
58,82 |
|
5 |
Нормативная трудовая активность работника, ЧНТ |
ФТАн |
11,88 |
|
6 |
Эффективная расценка (учет валентности), руб/ЧНТ |
РЭн |
70,59 |
|
7 |
Коэффициент трудозатрат (логарифмический) |
ДЕЛ |
299,50 |
|
8 |
Эффективная трудовая активность работника, ЧНТ |
ФТАэ |
13,44 |
|
9 |
Оценка месячной заработной платы (норма), руб |
ЗПнм |
16795 |
|
10 |
Отношение ФТА работник/среднерыночный работник |
ОТНрс |
1,68 |
Ответы на поставленные в задаче 4.3.1 вопросы.
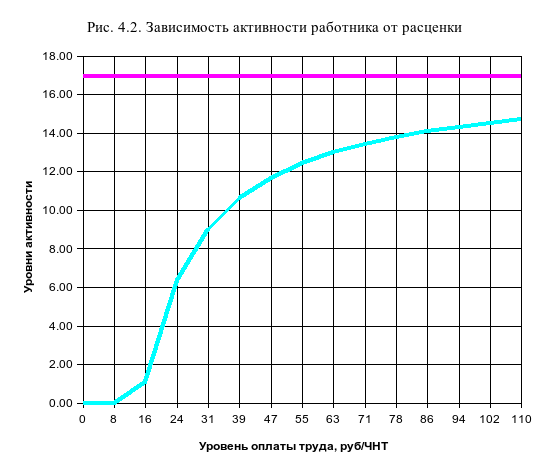
А) Среднедневной активности (ФТА) при оплате 1 ЧНТ равной 80 рублей.
По графику на рисунке 4.2. находим ФТА = 13.8 ЧНТ.
Б) Требуемую оплату 1 ЧНТ для выполнения работником 13 ЧНТ в среднем за рабочий день.
По графику на рисунке 4.1. находим р = 63 руб/ЧНТ.
В) Рассчитать уровни заработной платы работника в среднем за рабочий день и месяц по данным пп. А) и Б) (принять 20 рабочих дней в месяц).
По п. А. Среднедневная заработная плата – 13.8*80 = 1104 руб.; месячная – 22080 руб.
По п. Б. Среднедневная заработная плата – 13*63 = 819 руб.; месячная – 16380 руб.
Задача 4.3.2. Оптимизация бонуса менеджеров финансовой организации
С использованием математической модели активности работника и математической модели характеристики бизнеса финансовой организации в зоне ответственности менеджера провести расчеты оптимального процента вознаграждения (бонуса) от дополнительной прибыли. Исследовать эффект автоматного поведения менеджера в стимулирующей среде. Используя полученные результаты исследовать зависимость бонуса от валентности работника для следующих значений:
|
v=0,8 |
v=1 |
v=1,2 |
v=1,4 |
v=1,6 |
v=1,8 |
v=2 |
Расчеты провести с использованием программы в среде MS Excel (Файл «Активность менеджеров.xls»). Исходные данные представлены в таблицах 4.5, 4.6, 4.7.
Результаты расчетов системы стимулирования приведены в таблице 4.8. Собственнику фирмы аналитики рекомендуют установить процент бонуса от дополнительной прибыли фирмы для данного менеджера равный 12,3%. Тогда собственники обеспечат для себя среднедневной доход в объеме 2936,74 рублей.
Исследование влияния индекса валентности на результаты оптимизации представлены в таблице 4.9. Следует отметить, что строки этой таблицы по показателям совпадают с таблицей 4.8. Расчеты показывают, что собственникам целесообразно осуществить поиск менеджера с большим индексом валентности. Так менеджер, имеющий одинаковые с рассматриваемым трудовые показатели, но более мотивирован (v=1,4) увеличит прибыль собственникам на 5% за счет более интенсивного труда на уровне 70%.
Таблица 4.5. Трудовая характеристика менеджера
|
№ п/п |
Показатели |
Обознач |
Значение |
|
1 |
Продолжительность рабочего дня, час |
Тр |
12,00 |
|
2 |
Коэффициент интенсивности труда |
Кит |
1,50 |
|
3 |
Коэффициент квалификации |
Ккв |
1,95 |
|
4 |
Валентность работника |
Вр |
1,00 |
Таблица 4.6. Характеристика локального рынка труда
|
№ п/п |
Показатели для данной профессии |
Обознач |
Значение |
|
1 |
Средний коэффициент интенсивности труда |
Альфа |
0,70 |
|
2 |
Среднемесячная заработная плата, руб |
ЗПн |
2500,00 |
|
3 |
Среднемесячное число рабочих часов, час |
Тмес |
170,00 |
Таблица 4.7. Характеристика бизнеса
|
№ п/п |
Показатели для характеристики бизнеса |
Обознач |
Значение |
|
1 |
Потенциал чистой прибыли, руб. |
R |
4000,00 |
|
2 |
Нормативное значение чистой прибыли, руб. |
Rп |
3451,70 |
|
3 |
Нормативная активность работника, ЧНТ |
ФТАп |
35,10 |
Таблица 4.8. Результаты оптимизации системы оплаты труда
|
№ п/п |
Наименование показателей |
Значение |
|
1 |
Оптимальная оплата труда, руб/НТЧ |
12,61 |
|
2 |
Максимальный результат фирмы, руб. |
3347,58 |
|
3 |
Затраты на оплату труда, руб./раб. день |
410,83 |
|
4 |
Доля вознаграждения в валовой прибыли фирмы |
12,3% |
|
5 |
Чистый доход собственника, руб/раб день |
2936,74 |
|
6 |
Коэффициент интенсивности труда |
65,0% |
Таблица 4.9. Результаты оптимизации системы оплаты труда в зависимости от валентности
-
№ п/п
v=0,8
v=1
v=1,2
v=1,4
v=1,6
v=1,8
v=2
1
15,76
12,61
12,25
10,50
11,03
9,80
8,82
2
3347,58
3347,58
3451,70
3451,70
3551,55
3551,55
3551,55
3
513,54
410,83
430,15
368,70
414,78
368,70
331,83
4
15,3%
12,3%
12,5%
10,7%
11,7%
10,4%
9,3%
5
2834,03
2936,74
3021,56
3083,01
3136,77
3182,86
3219,73
6
65,0%
65,0%
70,0%
70,0%
75,0%
75,0%
75,0%
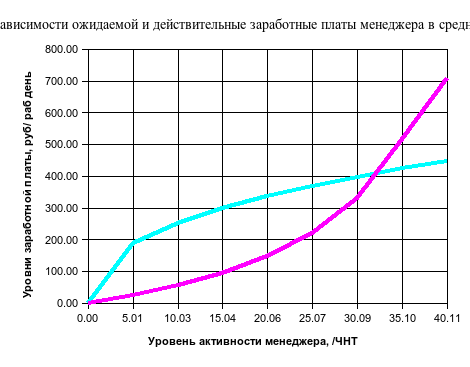
Исследование принципа автоматного поведения менеджера в стимулирующей среде, которое требуется согласно Задача 4.3.2. рекомендуется выполнить магистрантам самостоятельно. При этом следует учитывать гипотезу поведения работников: "Если работник получит фактическую заработную плату больше ожидаемой (рыночно справедливой), то он увеличит свою активность. Верно и обратное" Применение данного принципа иллюстрировано рисунком 4.2, на котором изображены ожидаемая (красная) и действительная (зеленая) заработные платы. Их пересечение – точка динамического равновесия в поведении менеджера.
Раздел 5. Аналитические исследования проблем корпоративного управления с использованием методов блочного программирования
Модель планирования объединения промышленных предприятий. Основы блочного линейного программирования.

В сложных системах (с двумя и более центрами принятия решений) кроме основных функций управления возникают дополнительные, такие как согласование и координация решений. Координация решения – это согласование деятельности, целей, зон ответственности, распределение общих ресурсов, совместного дохода.
Типичным примером сложной системы в экономике является система корпоративного управления – организационная модель, с помощью которой корпорация представляет и защищает интересы своих инвесторов. Тип применяемой модели зависит от структуры корпорации, существующей в рамках рыночной экономики, и отражает факт разделения функций владения и управления корпорацией. В общем случае, корпорация – объединение n юридических лиц плюс одна управляющая компания.
Управление корпорацией может осуществляться по двум схемам: централизованной и децентрализованной.
Централизованная схема характеризуется тем, что каждому предприятию выделяется часть объединенного ресурса. Решения «кому и сколько» принимает управляющая компания.

Рис. 5.1. Схема управления в централизованной системе
Децентрализованная схема: используется рыночный механизм, центр устанавливает внутрифирменные цены, лимиты. Каждое предприятие «покупает» часть ресурса, который необходим для достижения собственных целей. Решения о количестве приобретаемого ресурса предприятия принимают самостоятельно.
Тема 5.1. Модель планирования объединения промышленных предприятий
Рассматриваем объединение промышленных предприятий. Центр осуществляет управление объединением и сам не производит продукцию.
Каждое предприятие располагает для производства собственными ресурсами. Часть ресурсов передана в распоряжение управляющей компании (фонды оборотных средств, фонд развития, транспортные средства, основные производственные фонды).
Результат функционирования центра определяется результатами функционирования отдельных предприятий. Необходимо для каждого предприятия в рамках заданной номенклатуры определить объемы выпуска продукции такие, чтобы они были обеспечены локальными ресурсами, ресурсами объединения и давали объединению максимальную прибыль.
Экономический смысл модели планирования состоит в оптимизации планов производства объединения, при которых потенциальные возможности предприятий по прибыли максимально реализуются.
Пусть
объединение состоит из T
предприятий (блоков или бизнес-единиц),
каждое из которых выпускает продукцию
 видов, потребляя общие ресурсы отраслевого
назначения и ресурсы, являющиеся
«собственностью» предприятий.
видов, потребляя общие ресурсы отраслевого
назначения и ресурсы, являющиеся
«собственностью» предприятий.
Заданы
матрицы
 норм потребления локальных и ресурсов
объединения, векторы
норм потребления локальных и ресурсов
объединения, векторы
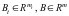 лимитов ресурсов локальных и объединения;
векторы
лимитов ресурсов локальных и объединения;
векторы
 коэффициентов дохода от реализации
продукции предприятием
коэффициентов дохода от реализации
продукции предприятием
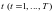 .
.
Пусть
неотрицательный вектор
 – план предприятия с номером t.
– план предприятия с номером t.
Модель планирования объединения имеет блочно-диагональную структуру вида:
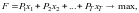 (5.1)
(5.1)
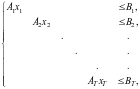 (5.2)
(5.2)
 (5.3)
(5.3)
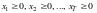 . (5.4)
. (5.4)
Пример. Построим модель (5.1)-(5.4) для T = 3. Пусть предприятия производят 2, 2 и 3 вида продукции соответственно (n1 = 2, n2 = 2, n3 = 3). На предприятиях имеется 3, 2 и 1 локальных ресурсов соответственно, а в объединении – 2 общих ресурса (m1 = 3, m2 = 2, m3 = 1, m = 2). Векторы переменных имеют вид:
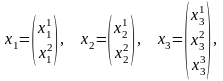
где
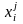 – объем j-го
вида продукции, производимого i-м
предприятием.
– объем j-го
вида продукции, производимого i-м
предприятием.
Модель планирования объединения в матричной форме будет иметь следующий вид:

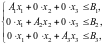 (5.5)
(5.5)
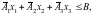
 .
.
Тема 5.2. Основы блочного линейного программирования
Рассмотрим методы решения задач оптимизации большой размерности (по числу переменных и ограничений). На практике такие задачи возникают при обосновании оптимальных решений в сложных производственных, экономических и социальных системах. «Проклятие размерности» характерно для большинства реальных задач математического программирования.
Задачи с условиями типа (5.2)-(5.4) называют задачами блочного линейного программирования. Блочность задачи планирования в объединении предприятий определяется тем, что локальные ресурсы используются только на своем предприятии. И если бы отсутствовали ограничения по ресурсам объединения, то данная задача распалась бы на несколько задач планирования каждого предприятия в отдельности.
Существуют два подхода к решению задач большой размерности:
– использование параллельных вычислений по алгоритмам математического программирования;
– использование методов декомпозиции больших экстремальных задач на стадии обоснования вычислительных алгоритмов – блочное программирование. Крупноразмерная модель сводится к нескольким моделям меньшей размерности. Получившиеся задачи решаются вместе по специальным правилам согласования.
Значение методов блочного программирования не ограничивается сферой разработки эффективных вычислительных схем. Они позволяют исследовать информационные процессы координации корпоративных решений в сложных системах.
Алгоритмизация вычислительных процессов выступает примером организации функционирования иерархических систем управления, в которых функции принятия решений распределены по участникам этих систем. Ведущую роль в принятии решений производственного характера играют элементы нижних уровней (блоков). Координирующий орган (центр) обеспечивает согласование решений по используемым ресурсам и производственным ограничениям. Главная роль центра сводится к обеспечению оптимальности решений блока по отношению к целевой функции системы в целом. Иерархическая система управляется путем передачи между элементами информационных потоков, объем которых существенно ниже размерностей задач, решаемых этими элементами.