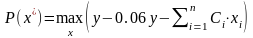; (2.8)

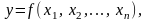
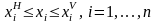. (2.9)

В задаче (2.8) – (2.9) 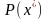– оптимальная годовая прибыль производственной деятельности фирмы с учетом налога, равного 6% от выручки; 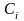– цена ресурса i (для ресурсов производства, учитываемых в стоимостном измерении, их цена принимается равной единице).

Можно показать (с учетом свойств производственной функции), что задача (2.8) – (2.9) относится к классу задач выпуклого программирования и ее решение можно получить в среде Excel.

---

Тема 2.4. Методы исполнения решений на различных этапах цикла принятия решений на примере задачи распределения ресурсов

На практике Центры принятия и реализации решений не являются идеально организованными и хорошо информированными. Тогда ожидаемые результаты не совпадают с реальными, особенно в ситуациях при больших по времени периодов реализации решений. Возникает необходимость совершенствования методических, математических и инструментальных методов принятия и реализации решений.

Выделим следующие этапы цикла принятия и реализации решений:

1. Сбор исходных данных и анализ экономической проблемы.

2. Обоснование оптимального решения и его принятие.

3. Реализация решения.

4. Оценка полученного результата и при необходимости внесение изменений в регламентные процедуры.

Характерным примером для данной темы является проблема распределения ограниченного ресурса. Она возникает в бюджетной сфере государственного и муниципального управления, производственных системах (корпорациях), при организации коллективных действий в социологии и политике и др.

Пусть Центр располагает ограниченным ресурсом в объеме 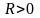и ставит задачу его распределения по 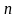исполнителям так, чтобы суммарная эффективность использования ресурса была максимальной. Обозначим объем ресурса, выделяемого исполнителю i (i=1,…,n). Будем считать, что вклад исполнителя i в суммарную эффективность зависит от объема выделенного ресурса и определяется выражением: 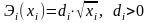, где – коэффициент, истинное значение которого Центр оценивает с погрешностью.

В предположении, что Центр идеально информирован, найдем оптимальное распределение 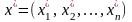решением следующей задачи:

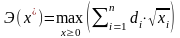; (2.10)

. (2.11)

Задание 2.4. Доказать, что в рассматриваемой формализации задачи при оптимальном решении Центр распределяет весь объем наличного ресурса и балансное ограничение (2.11) выполняется как равенство:

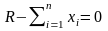
Решение задачи (2.10) – (2.11) найдем с использованием метода множителей Лагранжа (см. ссылку: https://ru.wikipedia.org/wiki/Метод_множителей_Лагранжа). Ограничение 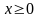пока не рассматриваем. Запишем функцию Лагранжа:

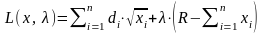. (2.12)

Составим систему из (n+1) уравнений, приравняв к нулю частные производные функции Лагранжа 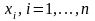по и по : .

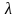Найдем решение первых n уравнений записанной системы в зависимости от :

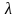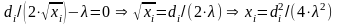. (2.13)

Рассматриваем последнее уравнение системы с учетом выражения (2.13):

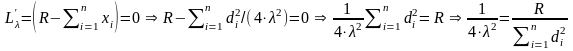. (2.14)

Из выражений (2.13) и (2.14) имеем:

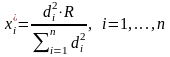. (2.15)

В рассматриваемом случае найденное решение системы (n+1) уравнений удовлетворяет ограничению 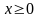и является оптимальным распределением ресурсов в задаче (2.10) – (2.11), поскольку она относится к классу задач выпуклого программирования.

Рассмотрим порядок использования полученных расчетов на практике контроля процессов принятия и реализации решений, которое можно провести только после завершения цикла (после полной или частичной реализации решения). Для этого предлагается использовать расчетные и фактические значения эффективностей распределения и использования ресурсов. Профессиональное расследование эффективностей проводится с использованием методов экономической безопасности.

---

Оптимальное распределение ресурса согласно (2.15) зависит от коэффициента : . Если при распределении ресурсов (не важна причина) использовались оценки , то фактические эффективности отличаются от истинных значений (которые аналитику следует восстановить). Согласно этапу п.4 цикла принятия и реализации решений необходимо внести изменения в регламенты. Но тогда необходимо выяснить причины отклонений: либо искажение информации, либо ошибки формализации проблемной ситуации, либо погрешности вычислений, либо объективное изменение условий принятия и реализации решений.

Тема 2.5. Типовые задачи, решаемые с использованием инструмента Excel «Поиск решения»

Поиск решений – надстройка (инструмент) Excel, которая помогает найти решение с помощью изменения значений целевых ячеек. Целью может быть минимизация, максимизация или достижение некоторого целевого значения. Проблема решается путем регулировки входных критериев или ограничений, определенных пользователем¹⁶.

В рассматриваемом курсе этот инструмент используется при оптимизации инвестиционного портфеля, при прогнозировании доходности вложения денежных средств в условиях нестабильной экономики (раздел 3) и при исследовании задач блочного программирования (раздел 5).

Задание 2.5. Рассмотреть порядок актуализации и примеры использования инструмента «Поиск решения» самостоятельно по указанной выше ссылке и с использованием программных средств лабораторных работ портфельного анализа.

---

Раздел 3. Математические и инструментальные методы портфельного анализа

Портфельный анализ. Модель Марковица. Формирование таблицы вариантов инвестиционных портфелей. Поддержка решений при оптимизации портфельных инвестиций в условиях стабильной и нестабильной экономики.

Тема 3.1. Портфельный анализ. Модель Марковица

Портфельная теория Марковица (англ. mean-variance analysis) — подход, основанный на анализе ожидаемых средних значений и вариаций случайных величин) — разработанная Гарри Марковицем методика формирования инвестиционного портфеля, направленная на оптимальный выбор активов, исходя из требуемого соотношения доходность/риск. Сформулированные им в 1950-х годах идеи составляют основу современной портфельной теории¹⁷.

Можно рассмотреть два различных подхода к формированию портфеля.

Первый связан с выбором активов, доходность которых стабильна, но существует не нулевая вероятность потери активов. Тогда цель портфельного анализа состоит в определении оптимального набора активов, при котором риски потерь являются минимальными. Данная стратегия портфельного анализа выражена рекомендацией: «не храните яйца (деньги) в одной корзине (в одном банке, одном активе)».

Второй подход, для которого применима теория Марковица, состоит в выборе совокупности компенсационных активов. Считается, что доходность активов является случайной величиной, но вероятности их полных потерь нулевые. Тогда цель портфельного анализа состоит в выборе совокупности активов, которая обеспечит высокую среднюю доходность (критерий 1) и минимальное отклонение уровня дохода от этого среднего (критерий 2 – риск должен быть минимальным). Снижение риска достигается использованием компенсационных активов, коэффициент корреляции доходностей которых является отрицательным. Модель Марковица позволяет выбрать оптимальный набор компенсационных активов с высокой средней доходностью.

При записи модели используются свойства математического ожидания и формула математического ожидания суммы случайных величин. Пусть для формирования оптимального портфеля выбраны n активов, доходность которых на период инвестирования – случайные величины с математическими ожиданиями 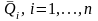и дисперсиями . Пусть 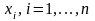– доли использования каждого актива в формируемом портфеле, которые удовлетворяют условиям:

. (3.1)

Тогда доходность портфеля 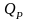на периоде инвестирования – случайная величина, которая зависит от доходности активов и определяется по следующей формуле:

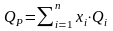. (3.2)

Найдем математическое ожидание (среднее значение) доходности :

.

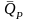Формулу для средней доходности портфеля можно записать в более наглядном виде:

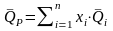. (3.3)

Из формулы (3.3) следует, что средняя доходность формируемого портфеля определяется средними доходностями активов и долями их включения в портфель.

---

Найдем выражение для дисперсии доходности портфеля :

.

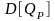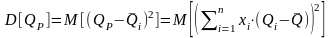Откуда получаем формулу для дисперсии портфеля в матричной записи:

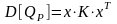. (3.4)

Здесь вектор – доли активов размерностью (1 × n); – вектор столбец долей активов размерностью (n × 1); – ковариационная матрица активов, которая отражает взаимозависимость доходностей выбранных активов, размерностью (n × n).

Модель Марковица предписывает выбор оптимального вектора 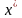долей, при котором средняя доходность портфеля должна быть не меньше заданной инвестором величины 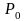(ограничение на критерий 1), а уровень риска отклонения доходности от средней величины был бы минимальным (минимизация критерия 2)¹⁸. Математически модель записывается с использованием выражений (3.1), (3.3), (3.4) в следующем виде. Найти 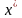из условий:

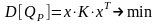; (3.5)

; (3.6)

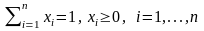. (3.7)

Задание 3.1. Доказать, что средний уровень доходности портфеля 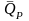изменяется в пределах: , т.е. от минимальной средней до максимальной средней 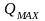доходностей выбранных активов:

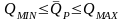. (3.8)

Учитывая утверждение в задании 3.1, аналитику следует рекомендовать инвестору указанные там границы для выбора требуемой доходности .

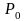Рассмотрим уровни риска для оценок реальной доходности портфеля. Обозначим границы доходности портфеля: %Низ и %Верх. Математическая статистика дает следующие доверительные интервалы для реальной доходности портфеля (см. формулу (3.2)):

%Низ 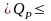%Верх, где %Низ = ; %Верх = . (3.9)

Здесь – квантиль распределения доходности, определяемый заданным уровнем доверительной вероятности (для нормального распределения 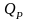и уровня значимости 5% ).

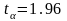Задание 3.2. Провести сравнение приведенных формул модели Марковица (3.5) – (3.7), границ изменения средней доходности портфеля (3.8) и уровней риска доходности (3.9) с формулами программы «Портфельный анализ СЭ.xls». Указать номера ячеек листа Excel, в которых вычисляются соответствующие величины.

Тема 3.2. Портфельный анализ. Формирование таблицы вариантов инвестиционных портфелей

Для использования модели Марковица на практике необходимо найти вероятностные оценки ее параметров (эта задача решается в Теме 3.3) и обосновать выбор уровня средней доходности портфеля 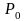. Эту задачу решаем в данном разделе путем формирования таблицы вариантов инвестиционных портфелей при разных значениях 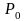. В таблице 3.1 приведены 10 вариантов портфеля, сформированного из 5 активов (расчеты проведены в среде Excel).

Таблица 3.1. Пример вариантов портфеля, полученных с использованием модели Марковица при изменении 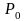равномерно в пределах 1,8% до 5.1%.

№ вар	А1	А2	А3	А4	А5	СД %	ДИ%	%Низ	%Верх
1	0,87	0,00	0,00	0,13	0,00	2,73%	1,03%	1,69%	3,76%
2	0,87	0,00	0,00	0,13	0,00	2,73%	1,03%	1,69%	3,76%
3	0,87	0,00	0,00	0,13	0,00	2,73%	1,03%	1,69%	3,76%
4	0,74	0,00	0,00	0,26	0,00	2,93%	1,06%	1,87%	3,98%
5	0,51	0,00	0,00	0,49	0,00	3,29%	1,20%	2,09%	4,49%
6	0,29	0,00	0,00	0,71	0,00	3,65%	1,44%	2,21%	5,09%
7	0,06	0,00	0,00	0,94	0,00	4,01%	1,73%	2,28%	5,75%
8	0,00	0,00	0,27	0,73	0,00	4,38%	2,13%	2,24%	6,51%
9	0,00	0,00	0,63	0,37	0,00	4,74%	2,59%	2,15%	7,33%
10	0,00	0,00	1,00	0,00	0,00	5,10%	3,07%	2,03%	8,17%

---

Смотрите также файлы

• Шаблон оформления ТЗ.pdf

• Управление проектами разработки ПО (теория).pdf

• Управление проектами разработки ПО (СРС).pdf

• Управление программами и проектами.pdf

• Разработка календарного плана-графика.pdf