Добавлен: 23.10.2018
Просмотров: 7342
Скачиваний: 22

94
При синусоидальном напряжении первичной обмотки трансформатора,
магнитный поток в сердечнике также будет синусоидальным:
t
sin
Ф
Ф
m
. (5.3)
Следовательно, ЭДС в первичной и вторичной обмотках:
)
2
t
sin(
Ф
w
t
cos
Ф
w
е
)
2
t
sin(
Ф
w
t
cos
Ф
w
е
m
2
m
2
2
m
1
m
1
1
(5.4)
Таким образом, ЭДС обмоток трансформатора отстают по фазе от потока на
/2. Действующие значения ЭДС обмоток трансформатора:
m
2
m
2
m
2
2
m
1
m
1
m
1
1
Ф
f
w
44
.
4
2
Ф
f
2
w
2
Ф
w
E
Ф
f
w
44
.
4
2
Ф
f
2
w
2
Ф
w
Е
(5.5)
ЭДС
1
е
уравновешивает основную часть напряжения источника питания
1
u
, ЭДС
2
е
создает напряжение
2
u
на зажимах вторичной обмотки трансформа-
тора (нагрузке). При замыкании цепи вторичной обмотки в ней возникает ток
2
i
, который образует собственный магнитный поток в сердечнике, складываю-
щийся с потоком первичной обмотки. В результате создается общий магнитный
поток сердечника, сцепленный с витками обеих обмоток трансформатора и оп-
ределяющий в них результирующие ЭДС
1
е
и
2
е
. Отношение ЭДС первичной и
вторичной обмоток, численно равное отношению числа витков первичной и
вторичной обмоток называется коэффициентом трансформации:
2
1
2
1
w
w
e
e
k
. (5.6)
Для понижающих трансформаторов
2
1
w
w
и
1
k
, для повышающих
2
1
w
w
и
1
k
.
Активная мощность, потребляемая трансформатором из сети:
1
1
1
1
cos
I
U
Р
. (5.7)
Активная мощность, отдаваемая потребителю:
2
2
2
2
cos
I
U
Р
. (5.8)
Если пренебречь потерями в трансформаторе, то приближенно
2
1
Р
Р
, и
тогда справедливы следующие выражения:
2
2
1
1
I
U
I
U
,
k
1
E
E
U
U
I
I
1
2
1
2
2
1
. (5.9)
То есть, если напряжение вторичной обмотки в k раз меньше напряжения
на первичной (понижающий трансформатор), то ток вторичной обмотки будет в

95
k раз больше и, наоборот для повышающего трансформатора ток вторичной
обмотки будет в k раз меньше тока первичной.
5.1.2 Уравнения электрического состояния и схема замещения
Основной магнитный поток трансформатора -
Ф
, замыкается через ферро-
магнитный сердечник и сцеплен с витками первичной и вторичной обмоток.
Помимо основного потока, токи обмоток создают магнитные потоки рассеяния
(рисунке 5.1), которые сцеплены с витками только одной обмотки – первичной
или вторичной. Эти потоки рассеяния наводят в обмотках трансформатора до-
полнительные ЭДС, которые называются ЭДС рассеяния -
1
р
е
и
2
р
е
. Таким об-
разом для первичной обмотки трансформатора напряжение питающей сети
уравновешивается ЭДС
1
е
от основного магнитного потока, ЭДС
1
р
е
от потока
рассеяния и падением напряжения на активном сопротивлении обмотки -
1
r
.
Так как напряжения, ЭДС и токи в первичной обмотке трансформатора являют-
ся синусоидальными, то можно записать уравнение электрического состояния
для первичной обмотки в комплексной форме:
1
1
1
р
1
1
I
r
E
E
U
. (5.10)
ЭДС рассеяния обычно учитывают с помощью дополнительной индуктивности
рассеяния
1
p
L
:
dt
di
L
е
1
1
р
1
р
,
1
1
p
1
1
p
1
p
I
x
j
I
L
j
E
. (5.11)
Тогда уравнение электрического состояния первичной обмотки запишется в
виде:
1
1
1
1
1
1
p
1
1
I
Z
E
I
r
I
x
j
E
U
, (5.12)
где
1
p
1
1
x
j
r
Z
- комплексное сопротивление первичной обмотки. Аналогично
может быть получено уравнение электрического равновесия для вторичной об-
мотки, с учетом того, что напряжение на вторичной обмотке равно ЭДС
2
е
на-
водимой основным потоком за вычетом ЭДС рассеяния вторичной обмотки
2
р
е
и падения напряжения на активном сопротивлении вторичной обмотки
2
r
:
2
2
2
2
2
2
p
2
2
I
Z
U
I
r
I
x
j
U
E
, (5.13)
где
2
p
2
2
x
j
r
Z
- комплексное сопротивление вторичной обмотки.
Падения напряжения в обмотках
1
1
I
Z
и
2
2
I
Z
составляют обычно не более не-
скольких процентов от напряжений
1
U
и
2
U
. Поэтому с некоторым приближе-
нием можно считать, что в нагруженном трансформаторе сохраняется равенст-
во
1
1
U
E
и
2
2
U
E
. При этом допущении амплитуда основного магнитного по-
тока:

96
dt
U
w
1
dt
E
w
1
Ф
1
1
1
1
, (5.14)
считается постоянной во всех режимах работы, так как напряжение питающей
сети
const
U
1
. Магнитный поток трансформатора определяется совместным
действием намагничивающих сил первичной и вторичной обмоток. Причем на-
магничивающая сила вторичной обмотки направлена противоположно намаг-
ничивающей силе первичной, то есть стремится размагнитить сердечник. Так
как магнитный поток в сердечнике постоянен, то и алгебраическая сумма на-
магничивающих сил обмоток должна оставаться постоянной, это равенство вы-
ражается уравнением намагничивающих сил трансформатора:
const
I
w
I
w
I
w
0
1
2
2
1
1
, (5.15)
где
0
1
I
w
- намагничивающая сила в режиме холостого хода, когда тока во вто-
ричной обмотке нет, а ток холостого хода первичной обмотки равен току на-
магничивания
0
I
. Если разделить левую и правую части уравнения (5.15) на
1
w
получим:
0
2
1
2
1
I
I
I
I
k
1
I
, (5.16)
где
2
2
I
k
1
I
- приведенный ток вторичной обмотки трансформатора.
В соответствии с уравнениями (5.12, 5.13, 5.16) построена векторная диа-
грамма трансформатора, работающего под нагрузкой (рисунке 5.2).
Построение векторной диаграммы удобно начинать с вектора основного
потока
m
Ф
. На векторной диаграмме используется приведенная ЭДС вторичной
обмотки
2
2
E
k
Е
в этом случае векторы
2
E
и
1
E
совпадают по величине и на-
правлению (отстают от вектора магнитного потока на
/2). При введении поня-
тия о приведенных ЭДС, напряжениях и токах необходимо найти приведенные
сопротивления вторичной обмотки, равные отношению приведенных напряже-
ний к приведенным токам:
2
2
2
r
k
r
,
2
р
2
2
р
x
k
x
. (5.17)
Таким образом, уравнение (4.13) для вторичной обмотки трансформатора на
векторной диаграмме заменяется соответствующим уравнением для приведен-
ных величин:
2
2
2
2
2
2
p
2
2
I
Z
U
I
r
I
x
j
U
E
, (5.18)
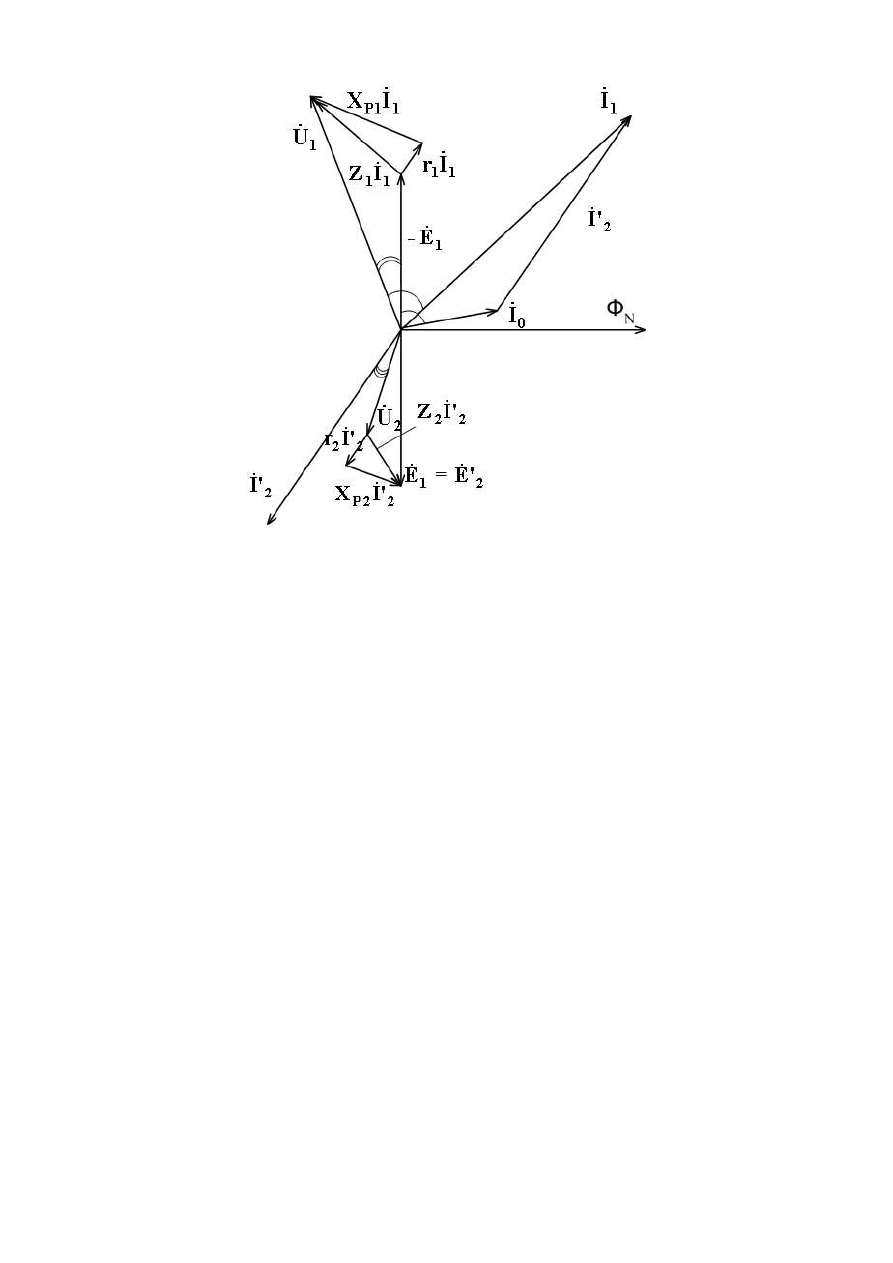
97
Рисунок 5.2 - Векторная диаграмма трансформатора,
работающего под нагрузкой
На векторной диаграмме для наглядности составляющие падения напряжения
на активных и индуктивных сопротивлениях первичной и вторичной обмоток
показаны преувеличенно большими, на самом деле их величины не превышают
нескольких процентов от напряжений
1
U
и
2
U
.
5.1.3 Схема замещения трансформатора
Расчеты токов и напряжений в трансформаторе могут быть сведены к
обычным расчетам цепей переменного тока. Для этой цели составляется экви-
валентная схема замещения трансформатора, процессы в которой описываются
теми же уравнениями, что и в реальном трансформаторе. В соответствии с
уравнениями (5.12, 5.16, 5.18) может быть построена схема замещения транс-
форматора (рисунок 5.3, а). Благодаря выполнению операции приведения маг-
нитную связь между обмотками трансформатора можно заменить электриче-
ской. При этом в схему замещения вводится цепь намагничивания, имеющая
сопротивление
0
0
0
x
j
r
Z
, которое рассчитывается так, чтобы выполнялось
условие
0
0
1
0
Z
I
E
E
.
Подобная схема замещения получила название Т-образной. Все парамет-
ры Т-образной схемы замещения не могут быть найдены экспериментальным
или расчетным путем. Поэтому на практике используется Г-образная схема за-
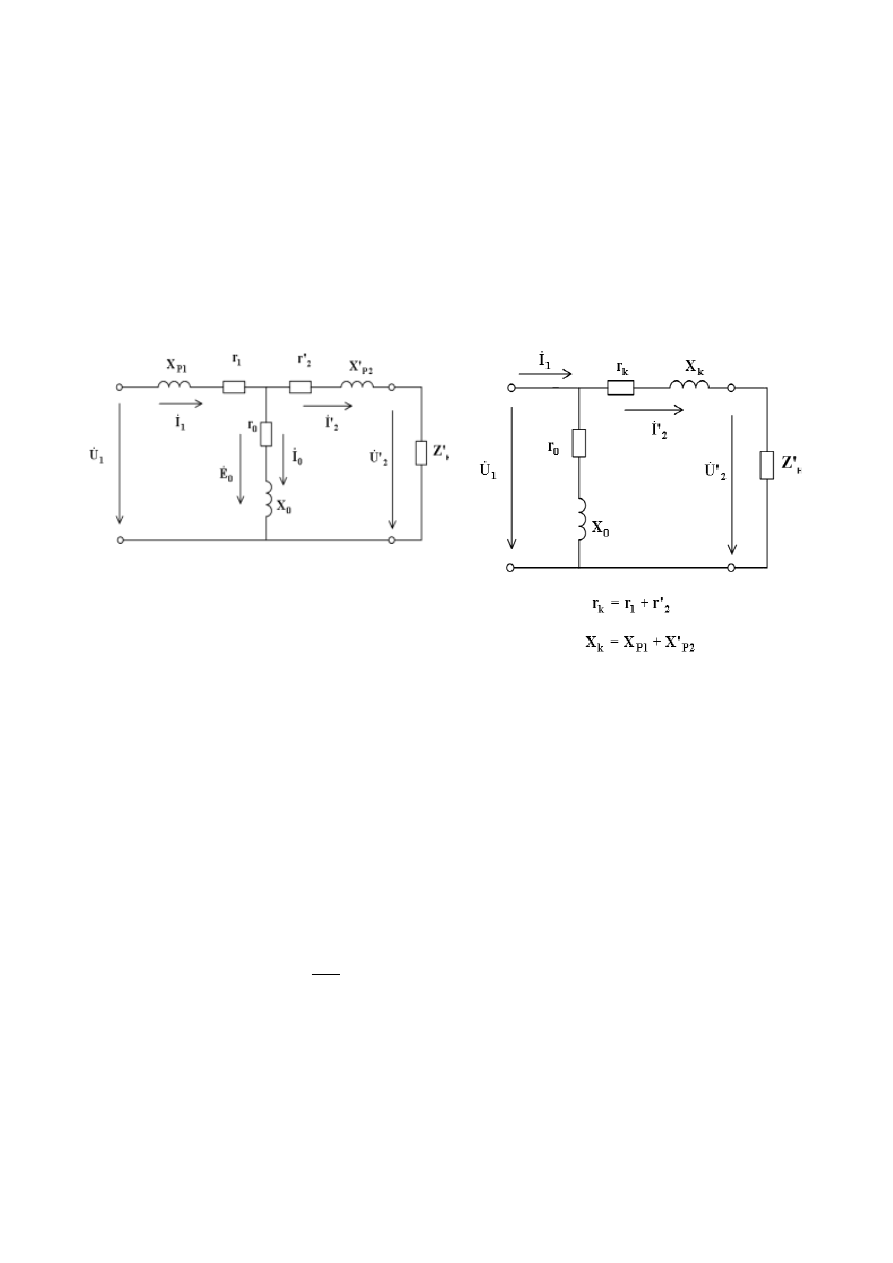
98
мещения трансформатора, в которой ветвь с током намагничивания
0
I
вынесена
к зажимам источника питания. Это сделано из предположения, что ток намаг-
ничивания остается постоянным во всех режимах работы. Такое преобразова-
ние схемы замещения вносит небольшую погрешность в расчеты, однако пара-
метры получившейся Г-образной схемы замещения (рисунок 5.3, б) могут быть
непосредственно измерены с помощью опытов холостого хода и короткого за-
мыкания трансформатора. Активные и реактивные сопротивления первичной и
вторичной обмоток на Г-образной схеме замещения обычно объединяются, где
2
1
K
r
r
r
,
2
р
1
р
K
x
x
x
.
а) б)
Рисунок 5.3 - Т-образная и Г-образная схемы замещения
трансформатора
5.1.4 Опыты холостого хода и короткого замыкания трансформато-
ра
Опыт холостого хода проводится в соответствии со схемой, показанной на
рисунке 5.4. У трансформаторов мощностью более 100 ВА относительная вели-
чина тока холостого хода при номинальном напряжении составляет:
)%
10
3
(
%
100
I
I
i
Н
1
0
x
. (5.19)