Добавлен: 25.10.2018
Просмотров: 2059
Скачиваний: 16
Не смотря на недостатки для размещения интернет магазина был выбран виртуальный хостинг.
Бэк-офис интернет магазина представляет собой небольшой офис, в котором работает не менее 8 сотрудников – руководитель, менеджеры по продажам и доставке, складской работник, бухгалтер, системный администратор, программист, маркетолог. На каждом рабочем месте установлен компьютер, также в офисе есть один выделенный канал в интернет с постоянным реальным ip адресом и доменным именем.
Для разработки вычислительной сети необходимо решить следующие задачи:
-
объединить все компьютеры в локальную сеть (LAN);
-
организовать печать со всех рабочих мест на сетевой принтер;
-
подключить и настроить Интернет - канал;
-
организовать доступ в Интернет со всех компьютеров локальной сети.;
-
защитить локальную сеть от внешних вторжений;
-
установить и настроить сетевые сервисы: WEB-сервер, почтовый сервер, файловый, FTP, прокси и т.д..
Схема вычислительной сети представлена на рисунке Ж.1 приложения Ж.
Поставленную задачу построения простой локальной сети мы будем решать на базе стека (набора) протоколов TCP/IP. Выбор оборудования для сети представлено в таблице 16, программного обеспечения – в таблице 17.
Таблица 16 – Технические средства вычислительной сети
|
Наименование ТС |
к-во |
|
Сервер Hewlett Packard NetServer E800 PIII-800/HDD 9,1Gb SCSI/128Mb ECC SDRAM/32x CD-ROM/Fast Ethernet NIC |
3шт |
HP QK703AQK703A, для сервера, 3.5", SAS, 3000 Гб, |
2шт |
|
Сетевой адаптер 3COM 3C905C PCI 10/100 |
8шт |
|
3Com 3C16470B-ME Baseline 10/100 Switch 16 Port |
2шт |
|
Кабель оптоволокно 9A/125/900 |
100м |
|
APC Smart-UPS, 390 Watts / 620 VA,Входной 230V / Выход 230V, Interface Port DB-9 RS-232 |
2шт. |
|
Сетевой принтер HP LaserJet 2100TN (C4172A) 10 стр/ мин сетев.10BaseT 8Mb |
1 шт. |
|
Рабочая станция Intel Core i7 3770 (3400Mhzx8)/ОЗУ 8Gb(4Gb)/2Gb Video Hd 4000 |
8 |
Таблица 17 – Сетевое программное обеспечение.
|
Тип программного обеспечения |
Наименование оборудования |
|
Сетевая операционная система |
MS Windows Server 2003 Standard Edition RUS |
|
Сервер баз данных |
SQL Server 2000 Standard Edition |
|
Антивирусная программа |
ESET NOD32 Smart Security Business |
|
Файрвол |
Outpost Firewall Pro 4.0 |
|
Почтовый сервер |
Microsoft Exchange |
5 НАДЕЖНОСТЬ АВТОМАТИЗИРОВАННОЙ СИСТЕМЫ
Надежность – это вероятность того, что при функционировании системы в течения некоторого периода времени не будет обнаружено ни одной ошибки; это вероятность работы системы без отказов в течения определенного периода времени, это функция воздействия ошибок на пользователя системы. Надежность не является внутреннем свойством программы, она во многом связана с тем, как программа используется.
5.1 Обзор модели надежности
Для количественной оценки показателей надежности программного обеспечения используют модели надежности, под которыми понимаются математические модели, построенные для оценки зависимости надежности от заранее известных или определенных в ходе выполнения задания параметров.
На рисунке 1 представлена одна из многих классификаций моделей надежности.

Рисунок 11 – Классификация моделей надежности
Модель надежности программного обеспечения подразделяются на аналитические и эмпирические. Аналитические модели дают возможность рассчитать количественные показатели надежности, основываясь на данных о поведении программы в процессе тестирования. Эмпирические – основаны на анализе структурных особенностей программного обеспечения и рассматриваю зависимость показателей надежности от числа межмодульных связей, количество циклов в модулях, отношения числа прямолинейных участков программы к числу точек ветвления. Аналитические модели делятся на две группы: динамические и статические модели. В динамических моделях появление отказов рассматривается во времени. В статических моделях не анализируют время появления отказов, а рассматривают зависимость количества оставшихся ошибок от числа тестированных прогонов или зависимость вероятности отказов от характеристики входных данных.
Для использования динамических моделей необходимо иметь данные о появлении отказов во времени. Если фиксируются моменты каждого отказа, то получим непрерывную картину появления отказов во времени (группа непрерывных динамических моделей). С другой стороны, может фиксироваться только число отказов за произвольный интервал времени. В этом случае поведение программного обеспечения может быть представлена только в дискретных точках (группа дискретных динамических моделей).
5.2 Основание выбора модели надежности
Для выбора надежности модели, при помощи которой будет осуществлять расчет надежности разрабатываемого программного обеспечения, проведем анализ существующих математических моделей на предмет их степени пригодности к использованию, при расчете надежности программного обеспечения автоматизированной системы «Учет товарооборота», с учетом специфичных свойств этого комплекса.
Выделение необходимой на модели будем производить, двигаясь по графу, представляющему классификацию математических моделей от корня к целевому узлу, обосновывая свой выбор при каждом переходе.
Первый шаг – выбор между аналитической и эмпирической типами моделей. Учитывая, что центральным модулем автоматизированной системы «Учет товарооборота» является база данных, предпочтительнее использовать аналитическую модель, в которой не учитываются структурные особенности программного обеспечения, являющиеся специфичными для процедурных языков программирования и абсолютно не свойственные реляционным базам данных.
Второй шаг – выбор между динамической и статической типами моделей. Все динамические модели опираются на время появления ошибок при проведении тестирования, которое не является обязательным параметром для статических моделей. Время появления ошибок является не желательной характеристикой при тестировании программного обеспечения для автоматизированной системы «Учет товарооборота» базирующийся на двух основных модулях – базы данных и запросная подсистема, при отсутствии расчетного модуля на процедурном языке программирования. Это связано с невозможностью применения к такой системе классического метода тестирования, заключающегося в проведении тестовых прогонов программного кода, с заданными входными данными. Такое ограничение закладывается специфической концепции баз данных и ошибок, возникающих при их проектировании, которые связанны, в большинстве случаев с различными структурными аномалиями при неверно спроектированной логической структуре базы данных, и возникают из-за незавершенного процесса нормализации, либо из-за искусственных нарушений концепции этого процесса, с целью повышения общего быстродействия базы данных. Поэтому единственно возможным методом тестирования является проведения ручного неформализованного метода тестирования, по средствам выполнения комплекса проверочных запросов, эффективность которых зависит от опыта и квалификации разработчика, при котором время появления ошибки перестает быть объективной, независимой характеристикой. Таким образом, очевидна необходимость использования статистической модели.
Шаг третий – выбор конкретной модели из существующих статических, аналитических моделей. Его можно осуществить исходя из имеющихся индивидуальных предпочтений, в связи с чем мной была избрана модель Миллса, главным достоинством которой, помимо непосредственных преимуществ, связанных со спецификой разрабатываемого программного обеспечения, является простота используемого математического аппарата, наглядность.
5.3 Методика расчета надежности по выбранной модели
Для выполнения расчетов, согласно модели Миллса, в исходную программу необходимо внести некоторое количество искусственно созданных ошибок. Эти ошибки вносятся в программу случайным образом, после чего делается предположение, что для ее собственных и внесенных ошибок вероятность обнаружения одинаковая и зависит только от их количества.
Тестируя программу в течения некоторого времени, собирается статистика об ошибках. В момент оценки надежности по протоколу искусственных ошибок все ошибки делятся на собственные и искусственные. Следующее соотношение, которое называется формулой Миллса, дает возможность оценить первоначальное число ошибок в программе – N:
N= (1)
(1)
где S – количество внесенных ошибок;
n – число найденных собственных ошибок;
V – число обнаруженных к моменту оценки искусственных ошибок.
Вторая
часть модели связана с проверкой гипотезы
от N.
Предположим, что в программе имеется K
собственных ошибок и внесем в нее еще
S
ошибок. В процессе тестирования были
обнаружены все S
внесенных ошибок и n
собственных ошибок. Тогда по формуле
Миллса мы предпо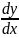 лагаем,
что первоначально в программе было N
равно n
ошибок. Вероятность, с которой можно
высказать такое предположение, можно
рассчитать по следующему соотношению:
лагаем,
что первоначально в программе было N
равно n
ошибок. Вероятность, с которой можно
высказать такое предположение, можно
рассчитать по следующему соотношению:
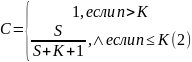
где C – мера доверия к модели, показывающая вероятность того, насколько правильно найдено значение N.
Эти два связанных между собой по смыслу соотношения образуют полезную модель ошибок: первое предсказывает возможное число первоначально имевшихся в программе ошибок, а второе используется для установления доверительного уровня прогноза. Однако формула (2) для расчета С не может быть использована в случае, когда не обнаружены все искусственно рассеянные ошибки. Для этого случая, когда оценка надежности производится до момента обнаружения всех рассеянных ошибок, величина С рассчитывается по формуле:
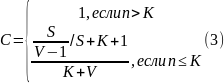
В действительности модель Миллса можно использовать для оценки N после каждой найденной ошибки. Предлагается во время всего периода тестирования отмечать на графике число найденных ошибок и, текущие значения для N. Достоинством модели являются простота применяемого математического аппарата, наглядность и возможность использования в процессе тестирования.
Однако она не лишена и рада недостатков, существенные из которых – это необходимость внесения искусственных ошибок (этот процесс плохо формализуем) и достаточно вольное допущение величины К, которое основывается исключительно на интуиции о опыте человека, проводящего оценку, т.е. допускает большое влияние субъективного фактора.
5.4 Расчет надежности автоматизированной системы
Для осуществления расчетов с использованием модели Миллса необходима формализовать метод внесения искусственных ошибок в тестируемый программный продукт, представленный для разрабатываемой подсистемы базы данных. Для этих целей мной был разработан соответствующий способ формализации ошибок, заключающийся в искусственном создании структурных нарушений целостности базы данных, влекущих генерирование неадекватной информации, в ответ на базовый комплекс спроектированных запросов. Такой способ формализации искусственных ошибок успешно моделирует реально возникающие ошибки в процессе проектирования подобных программных комплексов.
Перед началом тестирования в программу было внесено 5 искусственных ошибок, формализованных согласно приведенному выше методу. В результате тестирования было обнаружено 4 искусственно сгенерированных ошибок и 1 собственная. Используя формулу (1) из первой части модели Миллса, произведем расчет первоначального комплекса ошибок N, полученное равным 1.
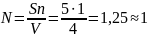
Для проверки корректности полученного значения N, необходимо применить формулу (3) из второй части модели Миллса, результат которой отражает значение степени доверия к данному значению N.
C
=
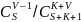
C=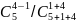 =
=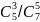

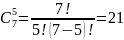

Полученное значение степени достоверности – С, равное 50%, к гипотезе о количестве существующих найденных ошибках в N в программном обеспечении, отражает неприемлемо слабый уровень правдоподобности N, в связи с чем его нельзя использовать для представления итоговой оценки надежности исходной программы. Таким образом, необходимо продолжить тестирование до получения более корректного значения N, степень правдоподобия которого будет равен не менее 90%.
Для достижения требуемого уровня доверия (90%) к предполагаемому количеству оставшихся ошибок N=1, выявленному по результатом применения первой части модели Миллса, необходимо сгенерировать не менее 20 искусственных ошибок, обнаружив их все при тестировании и не раскрыв более 1 собственной ошибки. Такой подход является не рациональным, ввиду большой трудоемкости процесса формализации большого количества искусственных ошибок, а так же из-за возникающего риска получить полностью неработоспособное программное обеспечение, неспособное выполнять даже базовый функционал. Поэтому будем вносить за один раз не более 10 искусственных ошибок, 5-7 из которых можно создать полностью самостоятельно, а в качестве остальных использовать найденные в процессе тестирования, выполняя перерасчет значений N, С для каждого выполненного теста.
Так же будем предполагать, что в ходе проведенных итераций тестирования будут устранены все собственные ошибки. Тогда для достижения приемлемого уровня доверия к N, необходимо будет выполнить тест с внесением 10 ошибок, целью которого будет являться обнаружение всех внесенных ошибок при количестве собственных равное 0. Расчет, выполненный согласно формулам (1) и (3), подтверждающий это утверждение, приведен ниже.
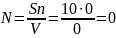
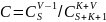
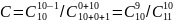
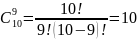


При проведении второго теста были использованы составленные на предшествующем этапе 5 искусственных ошибок и одна найденная собственная, помеченная как искусственно созданная. Таким образом, перед началом второго теста в программу было внесено 6 ошибок, в ходе которого было выявлено 4 искусственных и не одной собственной. Выполнения расчета количества оставшихся ошибок в программе N и соответствующего уровня доверия С производится аналогично соответствующем расчетам на первом этапе тестирования, согласно формулам (1) и (3). (Далее при выполнении аналогичных вычислений на последующих этапах тестирования, для краткости, не будем приводить формулы).




Полученный уровень доверия, равный 57% к значению N, предписывает продолжить тестирование.
На текущей, третьей итерации процесса тестирования внесем еще одну искусственную ошибку. Результаты теста следующие – обнаружено 6 из 7 искусственных и 2 собственных ошибки. Проведем расчет N, C:
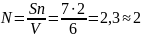
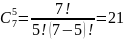
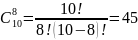
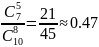
Не смотря на большее, по сравнению со вторым повтором количество внесенных и найденных ошибок, ввиду обнаружения 2-х собственных, значение С, уменьшилось до 47%, при N равном 2.
На четвертом повторе был использован комплекс из 9 искусственных ошибок, в состав которого включены 2 собственные, найденные на предыдущем этапе тестирования и помеченные как искусственные. В ходе проведения теста было обнаружено 8 из 9 внесенных ошибок и 1 собственная. Выполним расчет N, C:
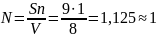

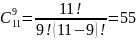

Полученное значение уровня доверия С равна 65%, позволяет утверждать, что оставшееся количество ошибок в тестируемом программном обеспечении близко к 1. Так же, в нашем распоряжении есть еще одна формализованная ошибка, которую в дальнейших тестах будем считать искусственной. Таким образом, мы приблизились к целевым условиям, дающим возможность провести тест, с участием 10 искусственных ошибок и достаточно весовым основаниям не встретить ни одной собственной ошибки на момент обнаружения всех искусственных, что позволит привести утверждение об отсутствии ошибок в исходном программном обеспечении с 90% доверия к этому утверждению.
Согласно приведенным выше рассуждениям, пятый повтор тестирования был проведен с учетом 10 искусственных ошибок, в результате, которого все 10 искусственных и не одной собственной ошибки. Расчет для этой целевой ситуации уже был проведен ранее, согласно которому N=0, при C=0,9.