Элементы теории корреляции

3.1.Функциональная, статистическая и корреляционная зависимости

Во многих задачах требуется установить или оценить зависимость случайной величины Y от одной или нескольких других величин. Рассмотрим сначала зависимость Y от одной случайной (или неслучайной величины) X. Две случайные величины могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми. При функциональной зависимости каждому значению X соответствует вполне определенное значение Y. На практике такая зависимость встречается редко, так как Y помимо X часто зависит от ряда других факторов, подчас остающихся скрытыми. Кроме того, при определении значений X и Y практически всегда присутствуют ошибки измерения. Поэтому общим видом зависимости является статистическая зависимость, когда изменение значений X ведет к изменению распределения случайной величины Y. В частности, статистическая зависимость может проявиться в том, что при изменении X меняется среднее значение Y. В этом случае статистическую зависимость называют корреляционной. Пусть, например, X – количество вносимых удобрений, а Y – урожай зерна. Тогда с ростом X урожайность в среднем увеличивается, но значение Y не определяется однозначно значением X, так как помимо количества удобрений на урожайность влияет ряд других факторов, часто случайных: погодные условия, количество осадков и т.д.

Пусть – условное математическое ожидание случайной величины Y (среднее значение случайной величины Y при фиксированном значении величины X, равном x). Функция

называется регрессией Y на X, а ее график – линией регрессии Y на X.

В простейшем случае эта зависимость линейная:

;

где коэффициент называется коэффициентом регрессии Y на X. Ее графиком является прямая линия.

Заметим, что если X и Y – независимые случайные величины, то

и уравнение регрессии примет вид, где b = M(Y), т.е. это будет линейная регрессия с коэффициентом регрессии, равным нулю, и горизонтальной линией регрессии.

Получение по выборке уравнения регрессии является важным элементом корреляционного анализа. В зависимости от конкретной задачи это уравнение можно искать в классе линейных или в более широком классе уравнений. Оно будет, вообще говоря, зависеть от выборки, и поэтому называется выборочным уравнением регрессии. Но, если класс, в котором ищется уравнение, выбран правильно, то с ростом объема выборки выборочная линия регрессии, в силу закона больших чисел, будет приближаться к истинной линии регрессии.

3.2.Парная корреляция. Коэффициент корреляции

Пусть имеется выборка из совместного распределения величин (Y,X), в которой величина Y принимает значения , а величина X – значения

причем пара встречается раз. Объем выборки

---

Такую выборку удобно представить в виде корреляционной таблицы, строки которой соответствуют значениям величины Y, а столбцы – значениям X. В клетке, образованной i-ой строкой и j–ым столбцом, записано значение .

По выборке уравнение прямой линии регрессии Y на X, получим:

.

Оценивая по выборке значения , мы тем самым оцениваем условное математическое ожидание случайной величины Y для каждого значения x. Эта оценка имеет вид Как известно, наилучшей оценкой математического ожидания является величина, минимизирующая средний квадрат разности между нею и элементами выборки. Поэтому в качестве оценки величин берутся такие их значения, которые минимизируют сумму квадратов отклонений наблюдаемых значений от их прогнозируемых математических ожиданий:

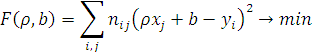
(ради краткости будем временно вместо писать ).

Условие минимума F является обращение в нуль частных производных:

Это дает систему двух линейных уравнений относительно

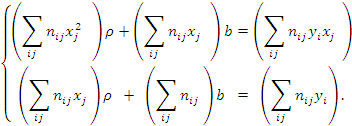
Поделив обе части каждого из уравнений на объем выборки n, получаем:

Второе из этих уравнений показывает, что выборочная линия регрессии проходит через точку . Ее уравнение, следовательно, может быть записано в виде:

Вычтя из первого уравнения системы второе, умноженное на , найдем выборочный коэффициент регрессии Y на X:

Стоящая в знаменателе величина есть выборочная дисперсия величины X. Обозначим ее через , где – выборочное среднее квадратическое отклонение. Через обозначим выборочное среднее отклонение величины Y. Тогда

.

Введем величину

которая называется выборочным коэффициентом корреляции величин X и Y.

Выразив коэффициент регрессии через коэффициент корреляции, получим уравнение регрессии в виде:

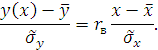
На практике уравнение регрессии Y на X можно рассматривать как соотношение, позволяющее прогнозировать значение случайной величины Y по известному значению величины X, используя в качестве прогноза значение

Изучим свойства выборочного коэффициента корреляции подробнее. Коэффициент корреляции симметричен относительно X и Y. Уравнение регрессии X на Y может быть записано с его помощью как

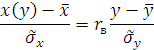
Рассмотрим величину

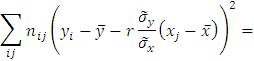
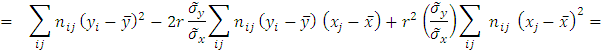
Исходное выражение, являясь суммой квадратов, неотрицательно. Поэтому Отсюда следует, что или причем в том и только в том случае, когда все выборочные пары точек лежат на прямой регрессии. Этот случай соответствует строгой линейной функциональной зависимости величин X и Y, когда значение y однозначно определяется значением x. Как уже отмечалось, на практике он встречается редко.

Если, напротив, случайные величины X и Y независимы, то математическое ожидание выборочного коэффициента корреляции как случайной величины равно нулю, и его вычисленное по выборке значение также будет близким к нулю. Поэтому модуль выборочного коэффициента корреляции можно рассматривать как меру линейной функциональной зависимости величин X и Y. Близость модуля коэффициента корреляции к единице говорит о том, что между X и Y имеется сильная линейная связь, и предсказание значения Y по X с помощью уравнения регрессии даст высокую точность.

---

Здесь следует отметить, что близость коэффициента корреляции к нулю не доказывает отсутствие функциональной связи между X и Y, а говорит лишь об отсутствии линейной функциональной зависимости. В качестве примера рассмотрим случай, когда случайная величина X распределена симметрично относительно нуля, а величина Y связана с X соотношением . В этом случае коэффициент корреляции величин X и Y равен нулю, несмотря на наличие между ними жесткой функциональной связи.

На практике, когда по выборке получено некоторое отличное от нуля значение выборочного коэффициента корреляции, может возникнуть вопрос, значимо ли это различие или, другими словами, имеется ли между ними X и Y линейная корреляционная связь. Можно сказать, что если величины X и Y нормальны и независимы, то величина

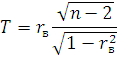
имеет распределение Стьюдента с степенями свободы. Для проверки значимости коэффициента корреляции при заданном уровне значимости по таблице критических точек распределения Стьюдента находят . Если значение величины T, вычисленное по выборке, , то коэффициент корреляции значим, и величины X и Y зависимы.

Пример. Среди владельцев иномарок было выбрано 100 человек. Из стоимости автомашин в тыс. у.е.(X) и годового дохода владельцев также в тыс. у.е.(Y) составлена корреляционная таблица:

Y	X
	5	10	15	20	25
10	10	5	-	-	-	15
20	5	10	5	-	-	20
30	5	5	10	5	-	25
40	-	5	5	10	-	20
50	-	5	5	5	5	20
	20	30	25	20	5

Найти коэффициент корреляции величин X и Y и уравнение прямой линии регрессии Y на X.

Решение. Используя корреляционную таблицу, найдем , ,

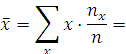
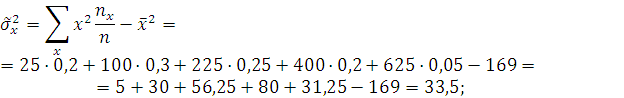
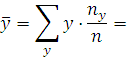
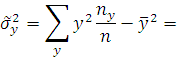
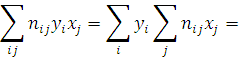
Проверяя значимость коэффициента корреляции по указанной выше схеме, получим:

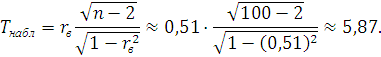
В предположении нормальности и независимости величин X и Y, критическое значение этой величины при уровне значимости найденное по таблице с равно т.е. имеет место , что свидетельствует о существовании линейной зависимости между X и Y.

Уравнение прямой линии регрессии Y на X запишется в виде:

или

Линия регрессии представлена на графике. Черными кружками отмечены выборочные значения. Размер кружков соответствует их частотам.

---

Смотрите также файлы

• Лекция 4. Неодинаковое число испытаний на различных уровнях.doc

• Лекция 3. Общая, факторная и остаточная дисперсии.doc

• Лекция 2. Элементы дисперсионного анализа.doc

• Лекция 1. Графический способ обработки опытных данных.doc

• Задание на контрольную работу №1.doc