Добавлен: 29.10.2018
Просмотров: 6930
Скачиваний: 24

Таблица 6.10.
Команды для символов-стрелок
←
\leftarrow
⇐
\Leftarrow
→
\rightarrow
⇒
\Rightarrow
←−
\longleftarrow
⇐=
\Longleftarrow
−→
\longrightarrow
=⇒
\Longrightarrow
↑
\uparrow
⇑
\Uparrow
↓
\downarrow
⇓
\Downarrow
↔
\leftrightarrow
⇔
\Leftrightarrow
←→
\longleftrightarrow
⇐⇒
\Longleftrightarrow
l
\updownarrow
m
\Updownarrow
%
\nearrow
&
\searrow
.
\swarrow
-
\nwarrow
7→
\mapsto
7−→
\longmapsto
←-
\hookleftarrow
,→
\hookrightarrow
(
\leftharpoonup
*
\rightharpoonup
+
\rightharpoondown
)
\leftharpoondown
\rightleftharpoons
Таблица 6.11.
Команды для функций
sin
\sin
arcsin
\arcsin
sec
\sec
cos
\cos
arccos
\arccos
csc
\csc
tan
\tan
arctan
\arctan
cot
\cot
sinh
\sinh
cosh
\cosh
max
\max
tanh
\tanh
coth
\coth
min
\min
log
\log
ln
\ln
lg
\lg
exp
\exp
sup
\sup
inf
\inf
lim
\lim
lim sup
\limsup
lim inf
\liminf
arg
\arg
ker
\ker
hom
\hom
det
\det
dim
\dim
gcd
\gcd
deg
\deg
Pr
\Pr
100
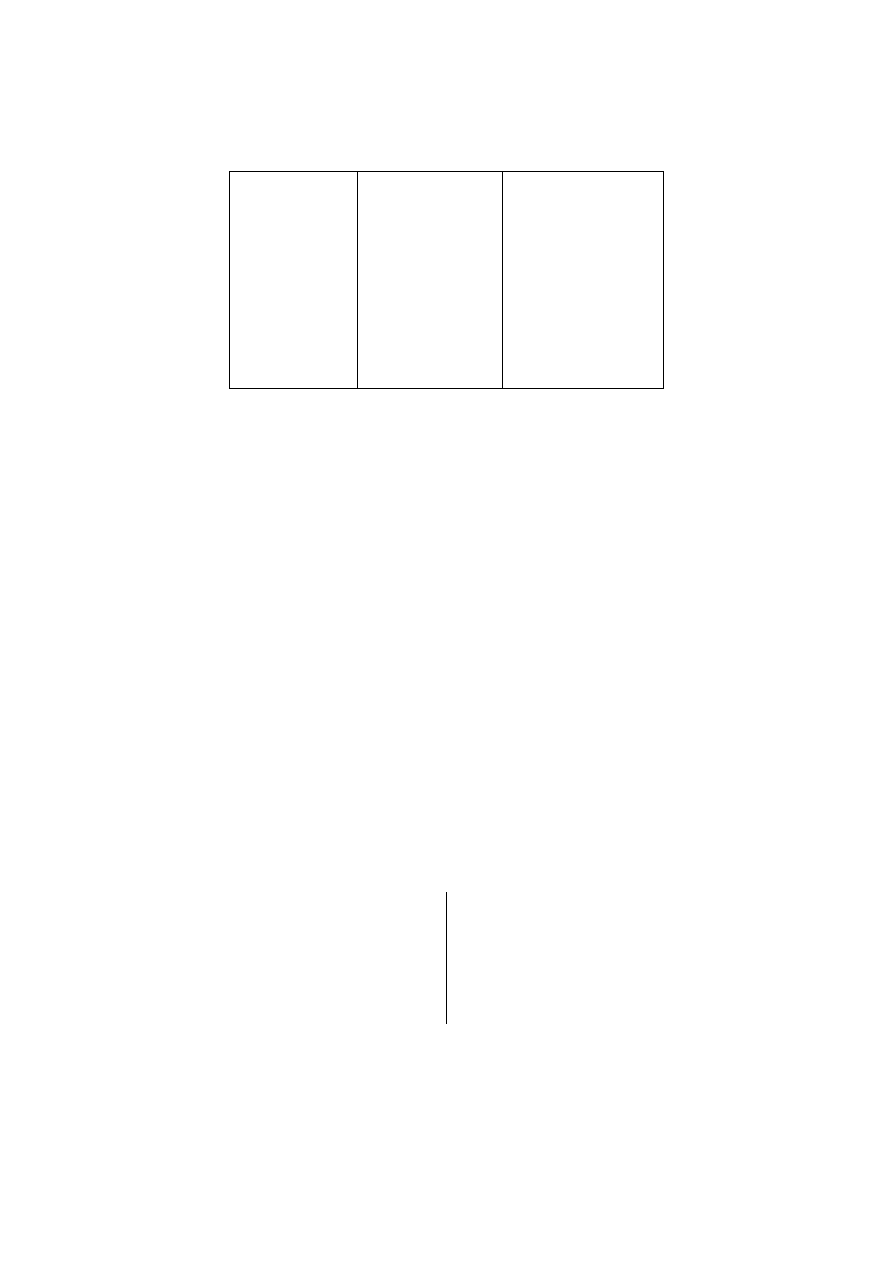
Таблица 6.12.
Команды для разных математических символов
ℵ
\aleph
0
\prime
∀
\forall
~
\hbar
∅
\emptyset
∃
\exists
ı
\imath
∇
\nabla
¬
\neg
\jmath
√
\surd
[
\flat
`
\ell
>
\top
\
\natural
℘
\wp
⊥
\bot
]
\sharp
<
\Re
k
\|
♣
\clubsuit
=
\Im
∠
\ angle
♦
\diamondsuit
∂
\partial
4
\triangle
♥
\heartsuit
∞
\infty
\
\backslash
♠
\spadesuit
Пример
.34 (определение пользовательских функций).
\DeclareMathOperator{\tg}{tg}|
\DeclareMathOperator*{\Lim}{Lim}
$$\Lim_{x\rightarrow k\pi}\tg^2x=0,
\forall k=0,1,\dotsc$$
Lim
x→kπ
tg
2
x = 0, ∀k = 0, 1, . . .
2.9. Прочие символы
В этой группе собраны все остальные символы. Если этих символов оказа-
лось недостаточно для записи выражения, можно воспользоваться символами
AMS-L
A
TEX’а.
3.
Основные структуры
3.1. Верхние и нижние индексы
Символы ‘
_’ и ‘ˆ’ обозначают, что следующий за ними символ является, соот-
ветственно, верхним или нижним индексом. Если в индексе должно быть несколько
символов, то их нужно взять в фигурные скобки (сгруппировать).
Примеры
.35 (использование индексов).
$x^{2y}$
x
2y
${x_y}_1$
x
y 1
$x_{2y}$
x
2y
$x^y^1$
ошибка
$x^y_1$
x
y
1
$x^{y^2}$
x
y
2
$x_y^1$
x
1
y
${x^y}^2$
x
y 2
$x_y_1$
ошибка
см$^2$
см
2
$x_{y_1}$
x
y
1
$x_{рад}$
x
${_i^jA_\|^{2y}}$
j
i
A
2y
k
$A^k{}_{ij}{}^l$
A
k
ij
l
101
Пакет amsmath вводит команду
\
substack{выражения }
для записи много-
строчных индексов. Для разбиения выражения на строки используется команда
\\
.
Пример
.36 (использование многострочных индексов).
X
0≤i≤m
0<j<n
P (i, j)
\begin{equation*}
\sum_{\substack{0\le i\le m\\
0<j<n}} P(i,j)
\end{equation*}
3.2. Корни
\
sqrt[n]{арг. }
— корень из арг. степени n.
Для корректировки положения указателя в пакете amsmath имеются команды
\
leftroot{n}
для сдвига влево (вправо, если n отрицательно) на n математических
длин и
\
uproot{n}
для сдвига вверх (вниз, если n отрицательно).
Примеры
.37 (задание корней).
√
x
3
√
x
β
√
k
β
√
k
$$ \sqrt{x} \quad \sqrt[3]{x} \quad
\sqrt[\beta]{k} \quad
\sqrt[\leftroot{-2}\uproot{2}\beta]{k} $$
3.3. Дроби
Небольшие дроби можно писать, используя знак ‘/’.
\
frac{числ. }{знам. }
—
дробь.
В AMS-L
A
TEX’е имеются дополнительные команды:
\
dfrac{числ. }{знам. }
и
\
tfrac{числ. }{знам. }
, которые форматируют дроби как в вынесенной формуле
и в текстовой строке, соответственно.
Примеры
.38 (задание дробей).
a
b
a
b
a
b
\frac{a}{b}\; \dfrac{a}{b}\; \tfrac{a}{b}
Непрерывную дробь можно получить с помощью команды
\
cfrac[сдвиг ]{числ. }{знам. }
.
В необязательном параметре можно указать сдвиг числителя:
l — влево, r — вправо.
102

Пример
.39 (непрерывная дробь).
1
√
2 +
1
√
2 +
1
√
2 +
1
√
2 +
1
√
2 + · · ·
\cfrac{1}{\sqrt{2}+
\cfrac{1}{\sqrt{2}+
\cfrac[l]{1}{\sqrt{2}+
\cfrac[r]{1}{\sqrt{2}+
\cfrac{1}{\sqrt{2}+\dotsb
}}}}}
3.4. Биномиальные коэффициенты
Биномиальные коэффициенты можно получить с помощью команды
\
choose
.
Пример
.40 (биномиальные коэффициенты в L
A
TEX’е).
n
n−k
{n\choose {n-k}}
В AMS-L
A
TEX’е имеются более удобные команды
•
\
binom{числ. }{знам. }
,
•
\
dbinom{числ. }{знам. }
,
•
\
tbinom{числ. }{знам. }
.
Последние две команды имеют тот-же смысл, что и аналогичные команды для дро-
бей.
Пример
.41 (биномиальные коэффициенты в AMS-L
A
TEX’е).
n
n−k
$\binom{n}{n-k}$
3.5. Размещение объектов друг над другом
В математических выражениях часто используют символы, расположенные друг
над другом, как, например, акценты или в бинарных операциях, операциях сравне-
ния, в выражениях со стрелками. Для размещения объектов друг над другом име-
ется команда
\
stackrel{верхний }{нижний }
.
Пример
.42 (размещения объектов друг над другом в L
A
TEX’е).
sin α
α→0
→ 0
103

$$ \sin\alpha
\stackrel{\alpha\rightarrow0}
{\rightarrow} 0 $$
Пакет amsmath предоставляет дополнительные команды:
•
\
overset{верхний }{нижний }
— для расположения объекта над символом;
•
\
underset{верхний }{нижний }
— для расположения объекта под символом;
•
\
sideset{верхний }{нижний }
— для расположения объекта слева и справа от
символа, используется, в основном для индексов.
Все эти команды можно использовать в сочетании друг с другом и другими коман-
дами.
\
overline{выражение }
и
\
underline{выражение }
используют для надчёрки-
вания и подчёркивания выражения, соответственно. Команда подчёркивания может
применяться и в текстовом режиме.
Команды
\
overbrace{выражение }
и
\
underbrace{выражение }
вставляют, со-
ответственно, над и под выражением горизонтальную фигурную скобку.
Пример
.43 (размещения объектов в AMS-L
A
TEX’е).
#
A * B
|
{z
}
∀x∈<
$$\overset{\looparrowright}{\underset{\forall
x\in\Re}{\underbrace{A\rightharpoonup B}}}$$
Команды
\
overleftarrow{выражение }
и
\
overrightarrow{выражение }
рису-
ют левую и правую стрелку над выражением, соответственно.
Пакет amsmath дополняет их следующими командами:
•
\
underleftarrow{выражение }
и
\
underrightarrow{выражение }
— для
стрелок под выражением;
•
\
overleftrightarrow{выражение }
и
\
underleftrightarrow{выражение }
—
для двунаправленных стрелок над и под выражением;
•
\
xleftarrow[ниж. ]{верх. }
и
\
xrightarrow[ниж. ]{верх. }
— для растя-
жимых стрелок, обязательный аргумент верх. – верхний индекс, необязатель-
ный — нижний.
Пример
.44 (размещения стрелок в AMS-L
A
TEX’е).
←−−−−−→
A
∀x∈<
−−−→
x B
B
$$\overleftrightarrow{{A\xrightarrow[x
\varsubsetneq B]{\forall x\in\Re}B}}$$
104