МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ»

Институт геологии и нефтегазодобычи

Кафедра автоматизации и вычислительной техники

ПРОВЕРКА ВЫБОРОЧНОГО РАСПРЕДЕЛЕНИЯ

Методические указания для лабораторных занятий

по дисциплине «Моделирование систем»

для студентов, обучающихся по направлению 220700.62

«Автоматизация технологических процессов и производств»

Составитель Ю.А. Ведерникова

Тюмень

ТюмГНГУ

2012

---

УДК 681.5.017

Проверка выборочного распределения: метод. указ. для студентов, обучающихся по напр. 220700.62 «Автоматизация технологических процессов и производств» / сост. Ю.А. Ведерникова; Тюменский государственный нефтегазовый университет.– 2-е изд., испр.– Тюмень: Издательский центр БИК ТюмГНГУ 2012.– 32 с.

Методические указания для лабораторных занятий рассмотрены и рекомендованы к изданию методическим семинаром кафедры автоматизации и вычислительной техники

«____» ____________ 2012 года, протокол № ____.

Аннотация

Методические указания и индивидуальные задания к лабораторной работе «Проверка выборочного распределения» по дисциплине «Моделирование систем» предназначены для студентов, обучающихся по направлению 220700.62 «Автоматизация технологических процессов и производств».

Лабораторная работа посвящена изучению методов обработки данных, полученных в результате научных или производственных экспериментов, путем расчета основных статистических характеристик случайных процессов и проверки выборочного распределения в среде MATLAB. Приведены варианты индивидуальных заданий.

---

СОДЕРЖАНИЕ

1. ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА 4

2. ГАУССОВЫ ПРОЦЕССЫ 4

2.1. Плотность вероятности 4

2.2. Основные статистические характеристики 5

3. ПРОВЕРКА ВЫБОРОЧНОГО РАСПРЕДЕЛЕНИЯ. 6

3.1. Гистограмма 7

3.2. Критерии согласия. 8

3.2.1. Критерий Пирсона. 9

3.2.2. Критерий Колмогорова. 10

3.3. Метод непараметрической статистики 11

4. ЗАДАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ 12

5. КОНТРОЛЬНЫЕ ВОПРОСЫ 13

6. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА 13

ПРИЛОЖЕНИЕ А 14

ПРИЛОЖЕНИЕ Б 15

ПРИЛОЖЕНИЕ В 16

ПРИЛОЖЕНИЕ Г 16

ПРИЛОЖЕНИЕ Д 17

ПРИЛОЖЕНИЕ Е 18

ПРИЛОЖЕНИЕ Ж 20

ПРИЛОЖЕНИЕ И 21

---

Цель работы: Изучение методов обработки данных, полученных в результате научных или производственных экспериментов, путем расчета основных статистических характеристик случайных процессов и проверки выборочного распределения в среде MATLAB.

ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА

На практике исследователь всегда располагает лишь ограниченным числом значений случайной величины, представляющим собой некоторую выборку из генеральной совокупности. Под генеральной совокупностью понимают все допустимые значения случайной величины. При анализе какой-либо технологической случайной величины, непрерывно изменяющейся во времени (например, температура, давление, расход и т.п.), под наблюдаемыми значениями случайной величины понимают значения технологического параметра в дискретные моменты времени, разделенные таким интервалом, при котором соседние значения можно считать полученными из независимых опытов.

Выборка называется репрезентативной (представительной), если она дает достаточное представление о генеральной совокупности. Если о генеральной совокупности ничего не известно, единственной гарантией репрезентативности может служить случайный отбор значений.

Из случайного характера выборок немедленно вытекает, что любое суждение о генеральной совокупности по выборке само случайно. Предположим, что в результате эксперимента получена выборка x₁, x₂, … ,x_n значений случайной величины X.

ГАУССОВЫ ПРОЦЕССЫ

Плотность вероятности

Метод статистического анализа процесса иллюстрирует рис.1.

В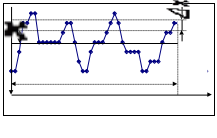
ероятность того, что значения случайного процесса попадают в интервал, ограниченный значениями х и х+∆х, после деления на ширину этого интервала ∆х называется плотность вероятности р(х). Если обозначить Р(х) вероятность того, что значения исследуемого случайного процесса меньше значения х, то плотность вероятности р(х) можно записать в виде выражения:

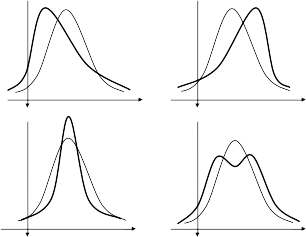
Гауссовы процессы служат моделью большинства встречающихся на практике случайных процессов и имеют нормальное распределение вероятностей. Присущая им функция плотности вероятности в графическом представлении имеет вид показанной на рисунке 2.

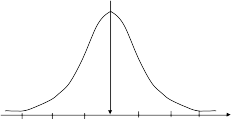
Плотность вероятности, соответствующая Гауссовому (нормальному) закону распределения, имеет вид:

Основные статистические характеристики

1. Среднее выборочное значение 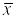вычисляется как сумма всех значений, деленная на их число.

2. Медиана m представляет собой значение, которое делит выборку пополам: число выборочных значений, меньших m , равно числу выборочных значений, больших m. При симметричном распределении значений переменной выборочное среднее обычно близко к значению медианы.

3. Среднеквадратичное или стандартное отклонение показывает насколько сильно выборочные значения разбросаны относительно среднего.

4. Дисперсия представляет собой квадрат стандартного отклонения.

5. Показатели асимметрии и эксцесса характеризуют степень несимметричности выборочного распределения относительно среднего значения и степень выраженности его центрального пика. Для нормального закона распределения эти показатели имеют следующие значения: асимметрия=0, эксцесс=3.

---

ПРОВЕРКА ВЫБОРОЧНОГО РАСПРЕДЕЛЕНИЯ.

Гипотезу о нормальности изучаемого распределения в математической статистике называют основной гипотезой.

Проверка основной гипотезы может быть проведена несколькими способами, которые дополняют друг друга:

• глазомерный метод в качестве предварительной субъективной оценки может быть осуществлен по рисунку гистограммы выборочного распределения с наложенной кривой плотности вероятности нормального распределения;

• проверка основной гипотезы по критериям согласия;

• проверка соответствия закона распределения с помощью методов непараметрической статистики.

Гистограмма

Гистограмма является общеупотребительной формой представления выборочного распределения. Для её построения диапазон изменения выборочных значений разбивают на k равных интервалов. Число интервалов k берут обычно в зависимости от объема выборки в пределах от 8 до 20. Число интервалов можно определить по полуэмпирической формуле:

(1)

Затем подсчитывают число значений, попадающих в каждый интервал. При графическом представлении гистограммы (рисунок 5) на каждом интервале строится прямоугольник, высота которого пропорциональна числу выборочных значений в интервале.

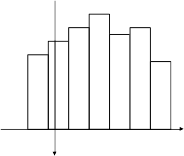
Если устремить объем выборки и число интервалов к бесконечности, то гистограмма будет приближаться к кривой плотности вероятности распределения значений исследуемой случайной величины.

Для расчета статистических характеристик и построения гистограммы в MATLAB имеются стандартные функции, описание которых приведено в таблице 1.

Таблица 1 – Функции MATLAB для расчета статистических характеристик и построения гистограммы

Функция	Значение
mean	Математическое ожидание
var	Дисперсия
std	среднеквадратичное отклонение
skewness	Асимметрия
kurtosis	Эксцесс
hist	построение гистограммы.

Пример М-файла для вычисления основных статистических характеристик выборки, сохраненной в векторе x1, и построения гистограммы приведен в приложении А.

Критерии согласия.

Проверка статистических гипотез

Под статистическими гипотезами понимают некоторые предположения относительно распределений генеральной совокупности той или иной случайной величины. Проверка гипотез осуществляется при помощи критериев значимости (критериев согласия), предусматривающих сопоставление некоторых статистических показателей, вычисляемых по выборке, со значениями этих показателей, определенными в предположении, что проверяемая гипотеза верна. При проверке гипотез подвергается испытанию 0-гипотеза в сравнении с альтернативной гипотезой , которая формулируется или подразумевается. Альтернативных гипотез может быть несколько.

Чтобы принять или отвергнуть гипотезу задаются уровнем значимости q. Наиболее употребительны уровни значимости 0,05; 0,02; 0,01; 0,1; 0,001. Уровню значимости соответствует вероятность . По этой вероятности, используя гипотезу о распределении оценки , находят квантильные доверительные границы, как правило, симметричные и . Если найденное по выборке значение попадает между и , 0-гипотеза принимается на заданном уровне значимости. Если же найденное значение оказывается меньше или больше , т.е. попадает в критическую область, гипотеза отвергается.

---

Смотрите также файлы

• Class_List(T)_Variants.pdf

• Проект по модулю ООП (3-й семестр).docx

• РГР по базам данных.rtf

• МетодУказания Электромонтер.docx

• Курсовая работа МУ.doc