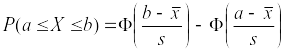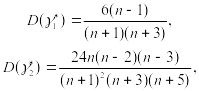При проверке гипотез можно совершать ошибки двух типов. Ошибка первого рода состоит в том, что отвергается гипотеза, которая на самом деле верна. Вероятность такой ошибки не больше принятого уровня значимости. Например, при , можно совершить ошибку первого рода в пяти случаях из ста. Ошибка второго рода состоит в том, что гипотеза принимается, а на самом деле она не верна. Вероятность ошибки второго рода зависит от характера проверяемой гипотезы, от способов проверки и от многих других причин, что сильно усложняет оценку. Эта вероятность тем меньше, чем выше уровень значимости, так как при этом увеличивается число отвергаемых гипотез.

Одну и ту же статистическую гипотезу можно исследовать при помощи различных критериев значимости.

Критерии согласия применяются для проверки гипотезы о предполагаемом виде закона распределения. Критерии согласия позволяют определить вероятность того, что при гипотетическом законе распределения наблюдающееся в рассматриваемой выборке отклонение вызывается случайными причинами, а не ошибкой в гипотезе. Если эта вероятность велика, то отклонение от гипотетического закона распределения следует признать случайным и считать, что гипотеза о предполагаемом законе распределения не отвергается.

Вероятностный характер критериев не позволяет однозначно принять или отвергнуть проверяемую гипотезу. Критерий позволяет утверждать, что гипотеза не противоречит опытным данным, если вероятность отклонения от гипотетического закона велика, или что гипотеза не согласуется с опытными данными, если вероятность мала. Чаще всего используется один из двух критериев согласия: критерий Пирсона ( -критерий ) и критерий Колмогорова.

Критерий Колмогорова реагирует на наибольшую разность между распределениями, которая обычно проявляется вблизи максимума функции плотности вероятности, поэтому он плохо предназначен для выявления различий на концах распределений.

Критерий Пирсона достаточно равномерно учитывает различия на всем диапазоне выборочных значений, однако требует большей осторожности применительно к непрерывным распределениям, поскольку результаты существенно зависят от объема выборки и от разбиения выборочного пространства на интервалы.

Критерий Пирсона.

Для применения -критерия (хи-квадрат) весь диапазон изменения случайной величины в выборке объема n разбивается на k интервалов (1). Число элементов выборки, попавших в i-й интервал, обозначим через n_i, вероятность попадания случайной величины в i-й интервал – p_i^*.

Результаты расчетов оформляются в виде таблицы

Интервал	Длина интервала	Число точек в интервале	Относительная частота
1 2 : i : k	(xmin, x1) (x1, x2) : (xi-1, xi) : (xk-1, xmax)	n1 n2 : ni : nk	р1* р2* : pi* : pk*
å		n	1

---

Построенная гистограмма выборочного распределения или общие соображения о механизме возникновения случайной величины служат основанием для выбора типа закона распределения. Параметры этого закона могут быть определены из теоретических соображений, или нахождением их оценок по выборке. На основании принятого закона распределения вычисляются вероятности p_i попадания случайной величины X в i-тый интервал. Величина, характеризующая отклонение выборочного распределения от предполагаемого, определяется формулой:

,

(2)

где k - число интервалов; n - объем выборки.

Сумма (2) имеет приближенно –распределение с f=k-c-1 степенями свободы, где с – число параметров гипотетического закона распределения, определяемых по выборке.

Для нормального распределения с=2, если и среднее и дисперсия определяются по данной выборке. Гипотеза о принятом типе закона распределения принимается на данном уровне значимости , если

(3)

, где определяется по таблице (Приложение Е) для выбранного уровня значимости и числа степеней свободы f. Если , делается вывод, что гипотеза не согласуется с выборочным распределением.

При использовании -критерия желательно, чтобы объем выборки был достаточно велик: , а количество элементов . Если какое-либо из n_i<5, то два или несколько соседних интервалов должны быть объединены в один. При этом соответственно уменьшается число степеней свободы.

Вероятности p_i попадания значений случайной величины в i-тый интервал для нормального закона распределения можно определить по формуле:

(4)

где –функция Лапласа.

При подсчете теоретических вероятностей p_i нужно считать, что крайний левый интервал простирается до , а крайний правый до .

Пример М-файла, позволяющего при помощи MATLAB проверить выборку на соответствие нормальному закону распределения по критерию Пирсона, приведен в приложении Б.

Критерий Колмогорова.

Для применения критерия согласия Колмогорова необходимо определить наибольшее абсолютное отклонение выборочной функции распределения Fn(x) от генеральной F(x):

(5)

Затем вычисляется величина :

D.

(6)

Квантили_n-1 распределения Колмогорова приведены в приложении Г.

Если вычисленное значение  меньше табличного _1-p, то гипотеза о совпадении теоретического закона распределения F(x) c выборочным F_n(x) не отвергается. При ³ _1-p гипотеза отклоняется (или считается сомнительной).

Для нормального распределения функция F(x) определяется по формуле

.

В MATLAB проверка по критерию согласия Колмогорова может быть проведена с помощью функции kstest. Пример М-файла для проверки выборки на соответствие нормальному закону распределения по критерию Колмогорова приведен в приложении В. Этот же программный файл позволяет нарисовать на одном графике выборочную функцию распределения F_n(x) и наиболее подходящую теоретическую F(x).

---

Метод непараметрической статистики

В случае выборок небольшого объема n<20 для проверки гипотезы о законе распределения можно использовать простые критерии, основанные на сравнении генеральных параметров распределения и их оценок, полученных по выборке. В качестве оцениваемых параметров удобнее всего брать моменты.

Нормальное распределение полностью определяется двумя параметрами – математическим ожиданием m_x и стандартом s_х . Все остальные моменты нормального распределения выражаются через математическое ожидание и стандарт. Для нормального распределения коэффициент асимметрии определяется по формуле:

(7)

и g₁=0, так как m₃=0.

Коэффициент экцесса, определяемый по формуле:

(8)

и тоже равен нулю, так как для нормального распределения

(9)

Выборочные коэффициенты экцесса и асимметрии определяются по формулам:

	(10)
	(11)

Распределение этих оценок сложны и мало изучены. Однако известны дисперсии этих величин:

(12)

где n- объем выборки.

Зная дисперсии D(g₁^*) и D(g₂^*), можно оценить, значимо ли выборочные коэффициенты асимметрии и экцесса отличаются от нуля. Если

	(13)
	(14)

то наблюдаемое распределение можно считать нормальным.

Хотя непараметрическая статистика обладает высокой универсальностью, но применять ее нужно осторожно, т.к. достаточно надежные результаты получаются лишь при очень больших n.

Нормальное распределение является наиболее изученным. Поэтому его стараются использовать и при изучении случайных величин, распределение которых отлично от нормального. Здесь могут быть два основных пути.

Первый путь заключается в переходе от заданной величины к другой, имеющей нормальное распределение, по определенной формуле, которую впоследствии можно будет учесть. Например, при изучении свойств случайной величины может оказаться, что нормальное распределение имеет ее логарифм (такое распределение называется логарифмически нормальным). Тогда вместо случайной величины X следует рассматривать случайную величину h=lg X, пересчитав все исходные данные применительно к новой величине. Получив с помощью формул нормального распределения все необходимые результаты для h, затем снова можно вернуться к X.

Другой путь заключается в том, чтобы распределение заданной случайной величины заменить приближенно нормальным (если это возможно). Второй путь особенно часто применяется при обработке экспериментальных данных, где обычно нет возможности установить распределение случайной величины с абсолютной точностью. Например, при обработке небольшого цифрового материала (микростатистика) можно, как правило, всегда пользоваться критерием нормального распределения, т.к. отклонения различных распределений друг от друга практически не заметны на малых выборках.

---

ЗАДАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ

1. Получить числовые данные у преподавателя. Полученные значения являются записями трех реализаций одного процесса (тремя выборками одной генеральной совокупности).

2. Для каждой выборки:

• построить график процесса и определить основные статистические характеристики (среднее, максимальное и минимальное значения, дисперсию, среднеквадратическое отклонение, медиану, коэффициенты асимметрии и эксцесса);

• построить гистограмму;

• проверить данные на соответствие нормальному закону распределения по критерию указанному преподавателем.

3. Сделать вывод о соответствии изучаемого процесса нормальному закону распределения.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какая гипотеза в математической статистике называется основной и почему?

2. Нормальный закон распределения.

3. Основные статистические характеристики и их значение.

4. Критерии согласия и их назначение.

5. Критерий Колмогорова и его особенности.

6. Критерий Пирсона и его особенности.

7. Метод непараметрической статистики и особенности его применения.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Ахназарова С.Л., Кафаров В.В. Оптимизация эксперимента в химии и химической технологии: Учеб. пособие для вузов. - М.: Высш. школа, 1978. – 319 с.

2. Поршнев С.В. Компьютерное моделирование физических процессов в пакете MATLAB. – М.: Горячая линия – Телеком, 2003. – 592 с., ил.

3. Иглин С.П. Математические расчеты на базе MATLAB.-СПб.: БХВ-Петербург, 2005.-640 с.: ил.

4. Дьяконов В.П. MATLAB 6/6.1/6.5+Simulink 4/5 в математике и моделировании. Полное руководство пользователя. М.: СОЛОН-Пресс.-2003-576 с.

5. http://chemstat.com.ru/node/9/ – Лекции по применению мат статистики.

6. http://www.statsoft.ru/home/textbook/esc.html – Элементарные понятия статистики.

7. http://www.statsoft.ru/home/textbook/ – Электронный учебник по статистике.

---

ПРИЛОЖЕНИЕ А

Текст М-файла, вычисляющего основные статистические характеристики выборки и строящего гистограмму

x=sort(x1(:)); % переформатировали столбец и рассортировали

n=length(x); % количество данных

xmin=x(1); % минимальное значение

xmax=x(n); % максимальное значение

Mx=mean(x); % математическое ожидание

f=n-1; % число степеней свободы

Dx=var(x); % дисперсия

Sx=std(x); % среднеквадратичное отклонение

Ax=skewness(x); % асимметрия

Ex=kurtosis(x)-3; % эксцесс

k=round(n^0.5); % число интервалов для построения гистограммы

d=(xmax-xmin)/k; % ширина каждого интервала

del=(xmax-xmin)/20; % добавки влево и вправо

xl=xmin-del;

xr=xmax+del; % границы интервала для построения графиков

fprintf('Число интервалов k=%d\n',k)

fprintf('Ширина интервала h=%14.7f\n',d)

[nj,xm]=hist(x,k); % число попаданий и середины интервалов

delta=xm(2)-xm(1); % ширина интервала

clear xfv fv xft ft % очистили массивы для f(x)

xfv=[xm-delta/2;xm+delta/2]; % абсциссы для эмпирической f(x)

xfv=reshape(xfv,prod(size(xfv)),1); % преобразовали в столбец

xfv=[xl;xfv(1);xfv;xfv(end);xr]; % добавили крайние

fv=nj/(n*delta); % значения эмпирической f(x) в виде 1 строки

fv=[fv;fv]; % 2 строки

fv=[0;0;reshape(fv,prod(size(fv)),1);0;0]; % + крайние, 1 столбец

xft=linspace(xl,xr,1000)'; % абсциссы для теоретической f(x)

ft=normpdf(xft,Mx,Sx);% значения для теоретической f(x)

col='bgmk'; % цвета для построения графиков

figure

plot(xfv,fv,'-r', xft,ft)%рисуем

set(get(gcf,'CurrentAxes'),...

'FontName','Times New Roman Cyr','FontSize',12)

title('\bfПлотности распределения')

xlim([xl xr]), ylim([0 1.4*max(fv)]) % границы рисунка по осям

xlabel('\itx') % метка оси x

ylabel('\itf\rm(\itx\rm)') % метка оси y

---

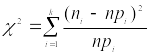Смотрите также файлы

• Class_List(T)_Variants.pdf

• Проект по модулю ООП (3-й семестр).docx

• РГР по базам данных.rtf

• МетодУказания Электромонтер.docx

• Курсовая работа МУ.doc