Добавлен: 15.11.2018
Просмотров: 2704
Скачиваний: 7

36
процедур (см. на рис. 1): декодирования-восстановления дискретных уровней
v�
k
j
по b�
k
m
, интерполяции и низкочастотной фильтрации. Фильтр-интерполятор –
это линейный фильтр с заданной импульсной реакцией g
0
(t
). В современных
ЦАП применяют ступенчатую интерполяцию с g
0
(t) = �1, t ∈ [0, T]
0, t ∉ [0, T]
, что при-
водит к увеличению длительности импульсов с величины τ
и
у v�
k
j
до величины
Т
0
у x�(t). Последующий ФНЧ сглаживает непрерывно-дискретное сообщение
x�(t), в результате чего образуется сигнал ĝ(t).
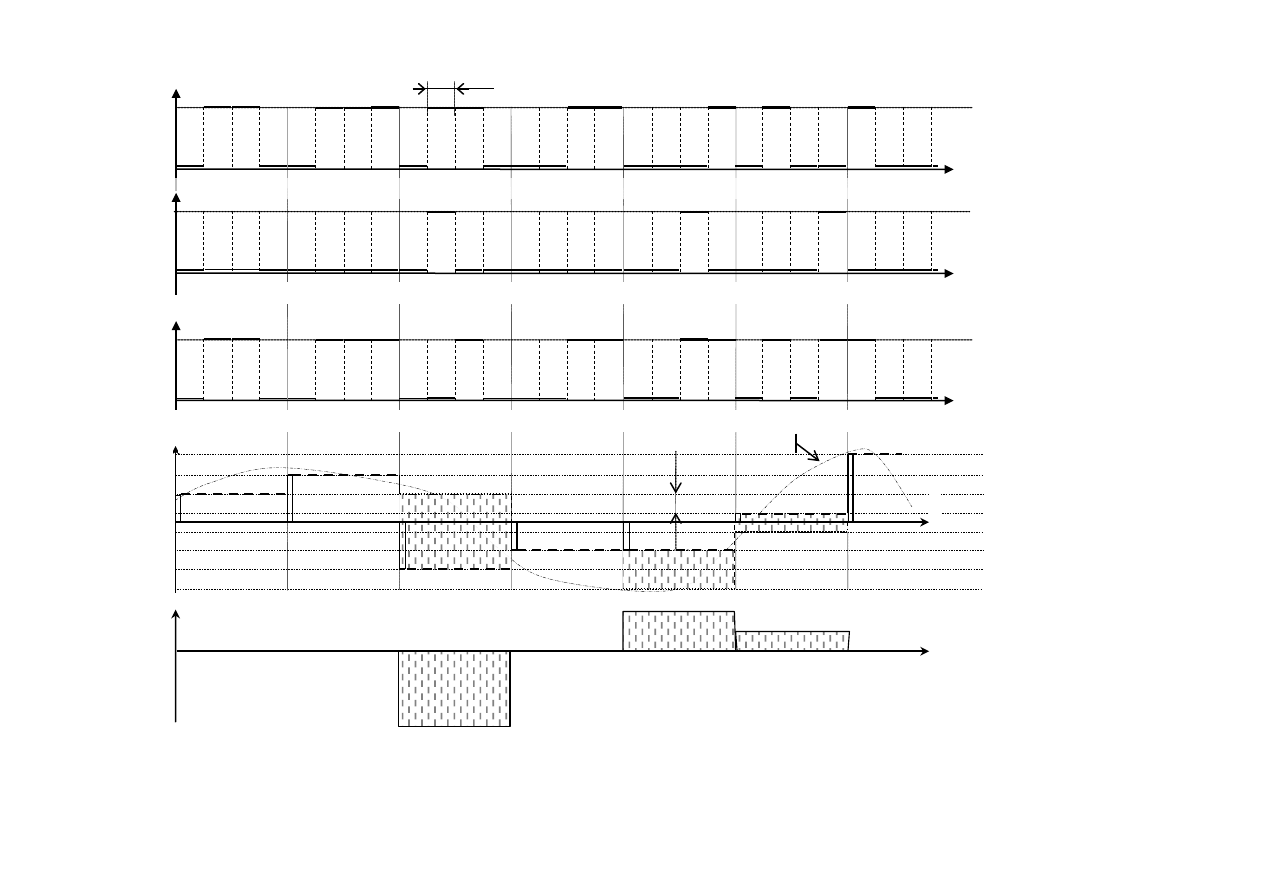
Эти процессы поясняет рисунок 8, на котором показан исходный сигнал
(рис. 8,а), помеха (вектор ошибок – рис. 8,б), принятый сигнал (рис. 8,в) и деко-
дированный сигнал (рис. 8,г).
Ошибки в двоичном канале связи приводят к несовпадению переданных
и принятых кодовых комбинаций сигнала ИКМ (см. рис. 8,а,б). На рис. 8,в по-
казана реализация последовательности блоков ошибок E
k
и принятая последо-
вательность b
k
μ
,
элементы которой определяются как ????????�
????????
= b
i
⊕
2
e
i
. Причем b
i
=
b�
i
при е
i
=
0 и b
i
≠ b�
i
при е
i
= 1,
???????? ∈ {1, ????????
�����}.
В декодере ЦАП двоичные ошибки в той или иной позиции кодовой
комбинации приводят к несоответствию восстанавливаемых v�
k
j
и передаваемых
v
k
i
уровней (см. рис. 8,г). Разность ξ
п
= v�
k
j
− v
k
i
называют шумом передачи. Реа-
лизация этого шума на выходе декодера (импульсы длительностью τ
0
) и на вы-
ходе интерполятора (импульсы длительностью Т) приведена на рис. 8,д.
Для определения скорости передачи информации R
L
по L-ичному ДКС
воспользуемся соотношением, аналогичным (35):
R
L
=
1
T
�H
y
− H
y/x
�.
Однако здесь х и у – это L-ичные уровни на входе и выходе L-ичного
ДКС. Используя выражения (36) и (37), но с учетом L-ичных уровней, и под-
ставляя их в выражение для R
L
, получаем:
R
L
=
1
T
∑
∑ p�v
k
i
, v�
k
j
�log
2
�
p�v
k
i
,v�
k
j
�
p�v
k
i
�p�v�
k
j
�
�
L
+1
j=1
L+1
i=1
,
где p(v
k
i
,
v�
k
j
) = p(v
k
i
)·p(
v�
k
j
/v
k
i
) = p
i
p
ij
= p(i, j) –
вероятность совместного наступле-
ния событий: v
k
i
на передаче и v�
k
j
на приеме;
p
i
, i
∈{1, ???????? + 1
����������} – распределение вероятностей, определяемое из соотношения (10);
p
ij
, i,j
∈{1, ???????? + 1
����������} – элементы матрицы переходных вероятностей L-ичного
ДКС, которые определяются выражениями:
p
il
= p(
v�
k
j
/v
k
i
) =
????????
ош
????????????????????????
(1 − ????????
ош
)
µ
−????????????????????????
, i,j
∈{1, ???????? + 1
����������},
где µ – значность кода (разрядность АЦП), µ = log
2
(L+1); d
ij
–
кодовое рассто-
яние между i-ой и j-ой кодовыми комбинациями; p
ош
–
вероятность ошибки в
двоичном симметричном ДКС.
В соотношении (38) распределение вероятностей принятых L-ичных
уровней определяются так:
p
j
= p(
v�
k
j
) = ∑
p�v
k
i
, v�
k
j
� = ∑
p
i
p
ij
L+1
i=1
L+1
i=1
, j
∈{1, ???????? + 1
����������}.
(38)
37
Рис. 8. Восстановление сигнала в ЦАП
τ
сим
v
k
j
v
L+1
v
L
…
v
2
v
1
г)
Δ
U
t /Δt
1
0
b
k
m
0 1 1 0 0 1 1 1 0 1 1 0 0 0 1 1 0 0 0 1 0 1 0 0 1 0 0 0
а)
t /Δt
0 1 2 3 … k k+1
1
0
0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0
б)
t /Δt
0 1 2 3 … k k+1
1
0
b
k
m
0 1 1 0 0 1 1 1 0 0 1 0 0 0 1 1 0 0 1 1 0 1 0 1 1 0 0 0
в)
0 1 2 3 … k k+1
Е
k
1000
0111
0110
0101
0100
0011
0010
0001
x(t)
t
t/Δt
ξ
пk
д)

38
Величина относительных потерь в скорости передачи информации по L-
ичному ДКС равна:
δ
R
=
R
И
−R
L
R
И
,
где R
И
–
максимальная производительность L-ичного источника, R
и
=
log
2
(L+1)
T
.
Оценим среднюю квадратическую погрешность (СКО) шума передачи
ξ̅
п
2
в L-ичном ДКС (см. рис. 8,д). Пусть в L-ичном ДКС был передан сигнал v
k
i
,
который на основании (6) равен:
v
k
i
= – 0,5
Δ
u
(L – 1) +
iΔ
u
.
Под действием помех он может перейти в
v�
k
j
= – 0,5Δ
u
(L – 1) +
jΔ
u
.
Тогда шум передачи ξ
пk
=
Δ
u
(j – k)
может быть представлен в виде по-
следовательности некоррелированных прямоугольных импульсов с нулевым
математическим ожиданием и со случайно распределенными амплитудами. На
выходе интерполятора длительность этих импульсов равна Δt.
Спектр плотности мощности шума передачи:
G
0
(ω) = 2Δtσ
и
2
�
sinωΔt/2
ωΔt/2
�
2
,
где σ
и
2
дисперсия (мощность) плотности распределения случайных амплитуд
импульсов, равная:
????????
и
2
= М{Δ
????????
2
(j − i)
2
} = Δ
u
2
∑
∑
p
i
L+1
j=1
p
ij
(j − i)
2
L+1
i=1
.
Полагая ФНЧ на выходе АЦП идеальным с полосой пропускания Δf
д
,
найдем СКО шума передачи путем интегрирования (39)
ξ̅
п
2
= ∫
G
п
(f)df
2πf
д
0
=
2σ
и
2
π
�si(π) −
2
π
�.
Здесь si(x) = ∫
sin(α)
α
dα
x
0
–
функция интегрального синуса [5]:
Выражение (40) для дисперсии амплитуд можно упростить, если истин-
ные вероятности ошибок р
ош
заменить усредненной величиной вероятности
ошибки:
p�
ош
=
1
L+1
∑
∑
p
ij
L+1
j=1
L+1
i=1
.
Тогда после ряда преобразований получаем:
????????
п
2
=
2Δ????????
2
[1−(1−????????
ош
)
????????
]
????????+1
∑ (???????? + 1 − ????????)
2
????????
????????
????????
????????=1
,
где F
i
, i
∈ {1, ???????? + 1
����������} интегральный закон распределения вероятностей, опреде-
ляемый из (11).
Подставляя (42) или (40) в (41), определяют СКО шума передачи.
Ввиду того, что погрешность фильтрации ξ
ф
(см. раздел 2.4), шум кван-
тования ξ
кв
(см. раздел 2.5) и шум передачи ξ
п
независимы друг от друга, то
суммарная СКО восстановления непрерывного сообщения x(t) будет равна
сумме СКО указанных процессов:
ξ̅
Σ
2
= ξ̅
ф
2
+ ξ̅
кв
2
+ ξ̅
п
2
.
(39)
(40)
(41)
(42)

39
Относительная суммарная СКО восстановления сообщения равна:
δ
Σ
= ξ
̅
Σ
2
σ
с
2
� .
Величина обратная 1/δ
Σ
есть отношение сигнал/шум, обеспечиваемое
системой передачи непрерывных сообщений.
СПИСОК ЛИТЕРАТУРЫ
1.
Лебедько Е. Г. Теоретические основы передачи информации. – СПб.: Лань, 2011.
2. Радиотехнические цепи и сигналы. Примеры и задачи: Учеб. пособие для
ВУЗов. Под ред. Гоноровского И. С. – М.: Радио и связь, 1989.
3. Баскаков С. И. Радиотехнические цепи и сигналы. Руководство к решению
задач: Учеб. пособие для ВУЗов. – М.: Высшая школа, 1987.
4.
Кнышев И. П. Аналого-цифровое преобразование сигналов в информацион-
ных системах. Уч. пос. – М.: РГОТУПС. 2008.
5.
Янке Е., Эмде Ф., Лёш Ф. Специальные функции. – М.: Наука, 1977.

40
Приложение 1