Добавлен: 15.11.2018
Просмотров: 2706
Скачиваний: 7

26
τ
сим
= Δt/µ = Δt/[log
2
(L+1)]
(см. рис. 2,д).
Ширина спектра элементарного прямоугольного импульса обратно про-
порциональна его длительности и, следовательно, ширина спектра цифрового
сигнала равна:
Δf
ИКМ
=
k
1
τ
сим
=
k
1
log
2
(L + 1)
Δt
= 2αf
g
k
1
log
2
(L + 1),
где k
1
–
коэффициент, равный 1,5 … 3; f
g
–
ширина спектра сигнала сообщения
x(t)
, а Δt = 1/2αf
ср
= 1/2
αf
g
.
2.6. Характеристики и параметры сигналов с дискретной модуляцией
Двоичные кодовые символы цифрового сигнала могут быть переданы с по-
мощью различных видов дискретной модуляции (манипуляции) параметров пере-
носчика. На рис. 5 показаны исходный модулирующий сигнал сообщения b
k
m
(рис.
5,
а) и модулирующий сигнал b
m
(t
) в виде биполярных импульсов, связанный с ис-
ходным сообщением простым соотношением b
m
(t) = 2b
k
m
–
1 (рис. 5,б). На рис. 5,в
изображена гармоническая несущая вида u(t) = U
M
cos
(2πf
н
t –
π/2), где: U
M
–
амплиту-
да; f
н
–
частота; π/2 – начальная фаза φ
0
(
при расчетах можно считать φ
0
= 0).
На рис 5 приведены сигналы дискретной амплитудной (ДАМ – рис. 5,г),
дискретной частотной (ДЧМ – рис. 5,д) и дискретной фазовой (ДФМ – рис. 5,е)
модуляции. Модулирующий сигнал сообщения в виде импульсов относитель-
ного кода b
от
m
(t),
необходимый для формирования сигнала дискретной относи-
тельной фазовой модуляции (ДОФМ), приведен на рис. 5,ж, (сам сигнал ДОФМ
изображен на рис. 5,и). При этом импульсы относительного кода формируются
по правилу b
от
m
(t) = b
m
(t)b
m
(t –
τ
и
)
, где b
m
(t –
τ
и
) –
сигнал сообщения, задержан-
ный на длительность символа τ
и
, причем b
i
,b
j
=
±1.
Рассмотрим аналитическое представление сигналов дискретной модуля-
ции (манипуляции) и их спектров. С этой целью в качестве модели манипули-
рующего импульсного сигнала сообщения b
от
m
(t)
примем сигнал вида:
????????
от
????????
= � ????????
0
= 1, −????????
и
≤ ???????? < 0;
????????
1
= −1,
0 ≤ ???????? < ????????
и.
Предполагая, что этот сигнал сообщения периодический с периодом
Т
и
=
2τ
и
, представим его тригонометрическим рядом Фурье (без учета фазовых
сдвигов):
????????
от
????????
=
2
????????
∑
1−cos ????????????????
????????
sin
????????????????
????????
и
∞
????????=1
???????? =
4
????????
∑
1
????????
∞
????????=1
sin
????????????????
????????
и
???????? , ???????? = 1,2,3, … . (13)
Как следует из (13), этот сигнал имеет только нечетные спектральные
составляющие на частотах:
f
k
=kf
и
= k/T
и
= k/2
τ
и
, k = 1, 3, 5, …;
τ
и
= 1/(2
Δf
g
log
2
L).
Сигнал ДАМ может быть представлен в виде:
S
ДАМ
(t) = 0,5U
m
[1 + b
m
(t)] sin ω
н
t = �
S
0
(t) = 0;
S
1
(t) = U
m
sin 2πf
н
t .
(14)
Поставляя (13) в (14), получаем следующее спектральное разложение
сигнала ДАМ:

27
S
ДАМ
(t) = 0,5U
m
sin 2πf
н
t + ∑
U
m
π(2k+1)
∞
k=0
[sin 2π(f
н
− (2k + 1)f
и
)t − sin2π(f
н
+ (2k +
1)f
и
)????????].
Ширина спектра сигнала ДАМ в два раза больше ширины спектра моду-
лирующего сигнала сообщения (цифрового сигнала):
Δf
ДАМ
= 2Δf
ИКМ
Сигнал ДЧМ с разрывом фазы представляется в виде:
S
ДЧМ
(t) = U
m
sin �2πf
н
t + ω
Д
� b
m
(t)dt
t
0
� = �S
0
(t) = U
m
sin 2πf
1
t ;
S
1
(t) = U
m
sin 2πf
2
t .
где 2πf
н
=
ω
н
–
несущая частота;
Δω
д
–
девиация (максимальное отклонение) частоты;
Δω
д
= 2
π(f
1
– f
2
)/2;
ω
2
=
ω
н
–
ω
Д
;
ω
1
=
ω
н
+
ω
Д
.
После ряда преобразований разложение сигнала ДЧМ по гармоническим
составляющим принимает следующий вид:
s
ДЧМ
(t) =
2U
m
m
ЧМ
π
∑
sin[π(m
ЧМ
+k)/2]
m
ЧМ
2
−k
cos 2π(f
н
+ kf
и
)t
∞
k=−∞
.
Здесь m
ЧМ
–
индекс частотной модуляции:
m
ЧМ
=
ω
Д
Δω
ИКМ
=
f
1
−f
2
2Δf
ИКМ
, f
1
> f
2
.
С достаточной для практических целей точностью ширина спектра сиг-
нала ДЧМ может быть определена так:
Δf
ДЧМ
= 2(m
ЧМ
+ 1)Δf
ИКМ
= |f
1
– f
2
| + 2f
ИКМ
.
Сигнал ДФМ представляется в виде:
S
ДФМ
(t) = U
m
sin[ω
н
t + m
ФМ
b
m
(t)] = �S
0
(t) = U
m
sin(2πf
н
t − π/2),
S
1
(t) = U
m
sin(2πf
н
t + π/2),
(19)
где m
ФМ
=
π
/2 индекс фазовой модуляции (максимальное отклонение фазы сиг-
нала ДФМ от начальной фазы несущей, принятой равной нулю).
Разложение сигнала ДФМ по гармоническим составляющим имеет сле-
дующий вид:
S
ДФМ
(t) = U
m
cos(m
ФМ
sin 2πf
н
) – ∑
2U
m
sin m
ФМ
π(2i+1)i
[sin 2π(f
н
− (2i + 1)f
ИКМ
)t +
∞
????????=0
sin 2π(f
н
+ (2i + 1)f
ИКМ
)t]. (20)
Ширина спектра сигнала ДФМ может быть определена следующим об-
разом:
Δf
ДФМ
= 2(m
ФМ
+ 1)Δf
ИКМ
= (2 +
π
)Δf
ИКМ
.
Спектр сигнала ДОФМ аналогичен спектру сигнала ДФМ.
По одному из выражений (15), (17) или (20) – в соответствии с заданием,
необходимо построить соответствующий амплитудный спектр сигнала дискрет-
ной модуляции на плоскости с координатами: амплитуда гармонической состав-
ляющей – частота (в МГц).
(15)
(16)
(17)
(18)
(21)

28
2.7. Характеристики и параметры узкополосного непрерывного
гауссовского канала связи
Модель узкополосного гауссовского НКС с шумами представляет собой
последовательное соединение входного идеального ПФ, линии связи без потерь
с аддитивной гауссовской помехой, имеющей равномерно распределенную
спектральную плотность мощности и выходного идеального ПФ. Центральная
частота ПФ совпадает с частотой несущего колебания (переносчика). Полоса
пропускания ПФ равна ширине спектра сигнала дискретной модуляции Δf
s
. В
полосе пропускания коэффициент передачи ПФ считаем равным единице.
Помеху с равномерной спектральной плотностью мощности называют
белым шумом. Спектральная плотность мощности этого шума равна G
ш
(
ω) =
N
0
,
ω ≥ 0.
Мощность гауссовского белого шума Р
ш
=
σ
ш
2
в полосе пропускания ПФ
можно определить как площадь прямоугольника с высотой N
0
и основанием Δf
s
:
Р
ш
= N
0
Δf
s
,
где Δf
s
определяют из соотношений (16), (18) или (21) в зависимости от вида
модуляции.
Учитывая (22) и то, что требуемое соотношение сигнал/шум (С/Ш)
h
2
=
Р
с
/Р
ш
на выходе детектора приемника известно, находим мощность сигнала
дискретной модуляции, обеспечивающую это С/Ш:
P
c
= h
2
P
ш
= h
2
N
0
Δf
s
.
На длительности посылки сигнал дискретной модуляции имеет вид гар-
монического колебания (см. рис. 5). Мощность гармонического колебания в
этом случае равна P
c
= U
m
2
/2
(это мощность, выделяющаяся на сопротивлении
1
Ом). Учитывая специфику формирования сигналов ДАМ, ДЧМ и ДФМ, полу-
чаем следующие соотношения для их мощностей и амплитуд, в среднем прихо-
дящихся на один двоичный символ модулирующего сигнала:
P
ДАМ
=
Р
с
/2,
U
m
=
�????????
ДАМ
,
P
ДЧМ
=
Р
с
,
U
m
=
�2????????
ДЧМ
,
P
ДФМ
= P
ДОФМ
= Р
с
,
U
m
=
�2????????
ДФМ
.
Пропускная способность НКС характеризует максимально возможную
скорость передачи информации по данному каналу. Максимум ищется по всем
возможным распределениям вероятностей сигналов, поступающих на вход
НКС. В теории электросвязи доказывается, что максимальная скорость переда-
чи информации по НКС будет обеспечена при таких методах кодирования и
модуляции, которые приводят к формированию в ПДУ сигнала с гауссовским
распределением мгновенных значений. При таком сигнале пропускная способ-
ность гауссовского НКС равна:
C =
Δ????????
кн
log
2
�1 +
????????
????????
????????
ш
� = Δ????????
кн
log
2
(1 + ℎ
2
),
где Δf
кн
–
полоса пропускания канала связи. Считаем Δf
кн
= Δf
s
.
В случае, когда сигнал на входе НКС отсутствует, в нем действует лишь
широкополосный шум в полосе Δf
ш
. При воздействии этого шума на полосовой
фильтр на его выходе будет шум в полосе частот Δf
s
.
(22)
(23)

29
Если отношение Δf
s
/Δf
ш
>>
1, то такой шум называют узкополосным.
Часто узкополосную гауссовскую помеху n(t) представляют в виде высокоча-
стотного гармонического колебания, модулированного по амплитуде и фазе.
Можно использовать две формы такого представления:
n(t) = N
ш
(t)cos[
ω
ш
t +
Ф(t)],
n(t) = N
шc
(t)
cosω
ш
t + N
шs
(t)
sinω
ш
t,
где N
ш
(t), N
шc
(t), N
шs
(t)
и Ф(t) – низкочастотные случайные процессы, связанные
соотношениями:
N
ш
(t) =
�N
шс
2
(t) + N
шs
2
(t), Ф(t) = arctg �
N
шс
(t)
N
шs
(t)
�,
N
шc
(t)
и N
шs
(t) –
синфазная и квадратурная составляющие помехи.
Функция распределения плотности вероятности (ФПВ) мгновенных зна-
чений низкочастотного шума описываются гауссовским распределением (см.
(1))
с числовыми характеристиками:
????????
ш
���� = ????????
шс
����� = ????????
ш????????
����� = 0, σ
N
ш
2
=
σ
N
шс
2
=
σ
N
шs
2
=
σ
ш
2
=P
ш
.
Огибающая N
ш
(t)
(случайно изменяющаяся амплитуда) гауссовской по-
мехи распределена по закону Рэлея, т. е.
W
Nш
(ν) =
ν
σ
ш
2
exp �
ν
2
2σ
ш
2
�, ν ≥ 0.
В случае, когда в НКС на детектор действует аддитивная смесь гармо-
нического сигнала и узкополосной гауссовской помехи, принятый сигнал мож-
но представить в виде:
z(t) = U
m
cos(
ω
c
t +
φ
0
) + n(t)] = U
*
m
(t)cos[
ω
c
t
+ Ф
*
(t)] = U
*
c
(t)cos(
ω
c
t) + U
*
s
(t) sin(
ω
c
t)
где U
*
c
(t) = U
m
cosφ
0
+ N
шc
(t)
и U
*
s
(t) = U
m
sinφ
0
+ N
шs
(t).
Функция распределения плотности вероятности мгновенных значений z(t)
в случае, если φ
0
распределена равномерно [W(φ
0
) = 1/2
π, –π ≤
φ
0
≤ π],
имеет вид:
W
z
(ν) =
1
π√2πσ
ш
∫ exp �−
(ν−U
m
cos ϕ)
2
2σ
ш
2
� dϕ
π
0
.
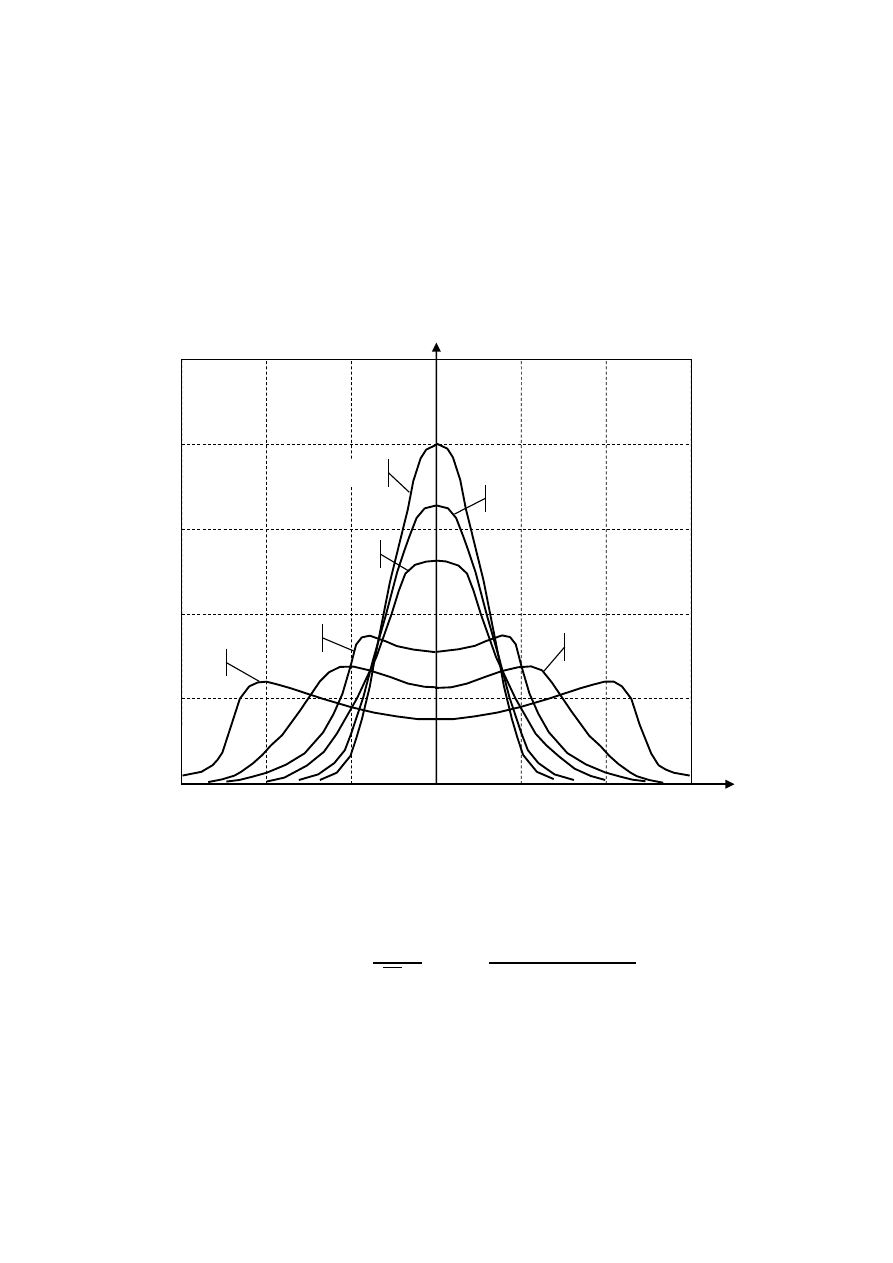
Графики этой ФПВ для нескольких значений параметра h = �
P
s
P
ш
=
U
m
√2σ
ш
приведены на рис. 6.
ФПВ огибающей U
*
m
(t)
принимаемого сигнала подчиняется обобщенно-
му распределению Рэлея (распределению Райса):
W
U
∗
(ν) =
ν
σ
ш
2
J
0
�
νU
m
σ
ш
2
� exp �− �
ν
2σ
ш
2
+ h
2
�� ν ≥ 0 ,
где J
0
(
β) – функция Бесселя первого рода нулевого порядка [5].
2.8. Оценка помехоустойчивости и эффективности приема сигналов
дискретной модуляции
Прием сигналов дискретной модуляции может осуществляться различ-
ными способами. В практике электросвязи широкое распространение получили
два вида приема – когерентный и некогерентный.
Когерентный прием (КП) предполагает использование в ПРУ когерент-
ного (синхронного) детектора, представляющего собой линейную систему с пе-
ременными параметрами.
(24)
(25)
30
Схема детектора состоит из перемножителя и фильтра нижних частот
(
ФНЧ). В перемножителе принятый сигнал z(t) умножается на опорное (син-
хронное) колебание u
г
(t) = U
г
cos(
ω
г
t +
φ
г
).
Рассмотрим выходной сигнал когерентного детектора.
Пусть на вход детектора поступает колебание в виде суммы гармониче-
ского сигнала и узкополосного гауссовского шума z(t) = U
m
cos(
ω
н
t +
φ
н
) + n(t).
Тогда при равенстве частот ω
г
=
ω
н
(условие синхронности) и единичном коэф-
фициенте передачи детектора на его выходе будет сигнал u
д
(t) = u
дs
(t) + u
дш
(t).
Здесь u
дs
(t) = U
m
cos(
φ
г
–
φ
0
) –
полезная (сигнальная) составляющая этого от-
клика, u
дш
(t) = N
шc
(t)cos
φ
г
+ N
шs
(t)sin
φ
г
–
шумовая составляющая этого отклика.
Рис. 6. Функция плотности вероятности смеси сигнала с шумом
Полезная составляющая является детерминированной, а шумовая состав-
ляющая имеет гауссовское распределение вероятностей. Следовательно, ФПВ от-
клика когерентного детектора при действии на входе сигнала и шума равна:
W
д
(u) =
1
√2πσ
ш
exp �−
[u−U
m
cos(φ
г
−φ
0
)]
2
2σ
ш
2
�.
При отсутствии на входе детектора сигнала отклик будет определяться
шумовой гауссовской составляющей c ФПВ, определяемой соотношением (26),
но при U
m
= 0.
При некогерентном приеме (НП) в ПРУ используется некогерентный де-
тектор, представляющий собой нелинейный (часто диодный) преобразователь и
ФНЧ. Этот тип детектора называют еще амплитудным детектором (детектором
W(U/σ
Ш
)
-6 -4 -2 0 2 4 6
U/σ
Ш
0,4
0,3
0,2
0,1
U
m
/σ
ш
= 0
0,4
1
2
5
10
(26)