Добавлен: 15.11.2018
Просмотров: 2705
Скачиваний: 7

31
огибающей), так как в отличие от когерентного детектора его отклик не зависит
от фазы входного сигнала.
Если на входе некогерентного детектора действует только узкополосная
гауссовская помеха n(t), то отклик детектора будет пропорционален ее огиба-
ющей и при единичном коэффициенте передачи детектора имеет ФПВ, описы-
ваемую законом Рэлея (см. (24)). При действии суммы гармонического сигнала
и узкополосного гауссовского шума ФПВ отклика некогерентного детектора
совпадает с ФПВ огибающей входной смеси, т. е. подчинено распределению
Райса (см. (25)).
Прием сигналов ДЧМ можно реализовать как с когерентным, так и с неко-
герентным детектированием. Если при приеме сигналов ДЧМ выделение посылок
разных частот производить двумя полосовыми фильтрами, то в каждом из каналов
можно также использовать либо когерентный, либо некогерентный детектор.
Для детектирования сигналов ДФМ используют фазовый детектор, яв-
ляющийся синхронным детектором.
Следует отметить, что прием сигналов ДФМ на практике сопровождает-
ся рядом трудностей: высокой сложностью обеспечения необходимой стабиль-
ности частоты ω
г
и фазы φ
г
опорного колебания; явлением обратной работы –
случайным изменением текущей фазы на противоположную (например, при
изменении дальности), что приводят к неправильному опознаванию кодовых
символов. Поэтому более широкое применение на практике нашла относитель-
ная фазовая манипуляция.
Детектирование сигналов ДОФМ производится двумя методами: мето-
дом сравнения фаз или методом сравнения полярностей. При методе сравнения
фаз в фазовом детекторе сравниваются фазы текущего и предыдущего, задер-
жанного на время τ
и
, колебаний. В методе сравнения полярностей производится
сравнение продетектированных текущей и задержанной на время τ
и
, посылок
принимающих два значения: +1 или –1.
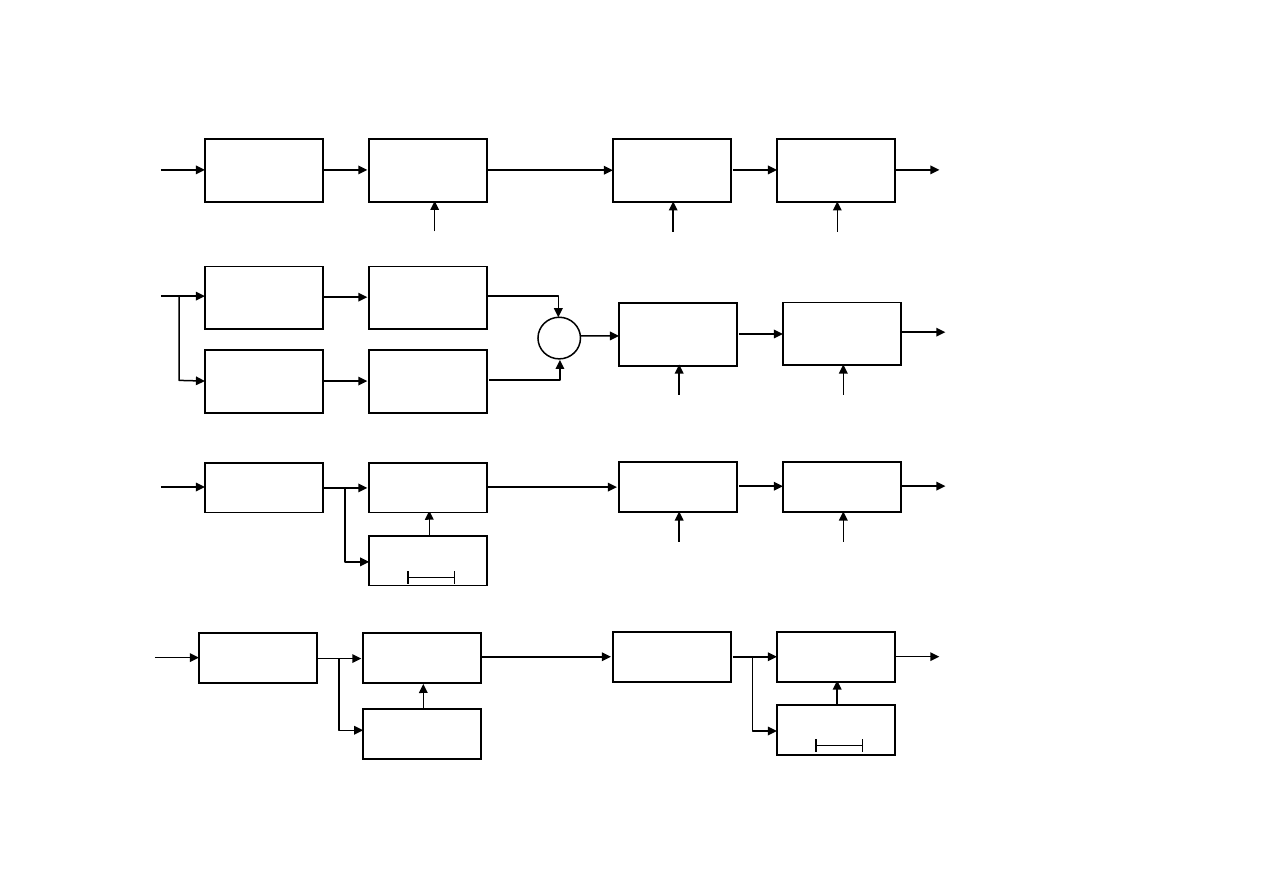
Схемы приемников сигналов различных видов дискретной модуляции
приведены на рис. 7. На схемах использованы следующие обозначения:
ППФ – полосно-пропускающий фильтр на частоте f
н
с полосой Δf
ДАМ
или Δf
ДФМ
;
ППФ1 – полосно-пропускающий фильтр на частоте f
1
с полосой Δf << f
1
– f
2
;
ППФ2 – полосно-пропускающий фильтр на частоте f
2
с полосой Δf << f
1
– f
2
;
ВУ – вычитающее устройство;
ЛЗ – линия задержки на время τ
и
;
ФОН – формирователь опорного напряжения.
Здесь полагается, что f
1
> f
2
.
Кроме описанных выше детекторов, имеются элементы последетектор-
ной обработки. К ним относятся дискретизатор и решающее устройство (РУ).
На дискретизатор наряду с откликом детектора u
д
(t
) подаются дискретизирую-
щие импульсы с периодом Δt, необходимые для взятия одного отсчета в сере-
дине посылки длительностью τ
и
.
32
а) Приемник сигналов с ДАМ
�1, ????????
????????
≥ ????????
0
0, ????????
????????
< ????????
0
б) Приемник сигналов с ДЧМ
�1, ????????
????????
≥ ????????
0
0, ????????
????????
< ????????
0
в) Приемник сигналов с ДОФМ (метод сравнения фаз)
�1, ????????
????????
≥ ????????
0
0, ????????
????????
< ????????
0
г) Приемник сигналов с ДОФМ (метод сравнения полярностей)
�1, ????????
????????
≥ 0
0, ????????
????????
< 0
Рис.7 Схемы приемников дискретной модуляции
u
г
(t)
δ
τи
(t)
z(t)
U
0
ППФ
Детектор
Дискретизатор
РУ
ВУ
δ
τи
(t)
z(t)
U
0
= 0
ППФ2
Детектор
ППФ1
Детектор
Дискретизатор
РУ
δ
τи
(t)
z(t)
U
0
ППФ
Детектор
ЛЗ
τ
и
РУ
Дискретизатор
z(t)
ППФ
Фазовый
детектор
ЛЗ
τ
и
Сравнение
полярностей
РУ
ФОН

33
В РУ отсчеты U
k
сравниваются с пороговым напряжением U
0
и прини-
мается решение – передана «1», если U
k
≥ U
0
, или передан «0» если U
k
< U
0
.
Из-за воздействия помех на сигнал в канале связи РУ может принимать
неправильные (ошибочные) решения. Ошибочные решения бывают двух видов:
переход 0 в 1 (передавался 0, но РУ выдало решение 1 ), характеризующийся
условной (апостериорной) вероятностью ошибки p(1/0), и переход 1 в 0 (переда-
валась 1, но РУ выдало решение 0), характеризующийся условной вероятностью
ошибки p(0/1).
За количественную меру помехоустойчивости в системах электросвязи
принимают среднюю вероятность ошибки на один бит:
р
ош
= р(0)р(1/0) + р(1)р(0/1).
При равенстве априорных вероятностей р(0) = р(1) = 0,5, а также при ра-
венстве условных вероятностей р(0/1) = р
1
=
р(1/0) = р
0
(условия симметричного
ДКС), средняя на бит вероятность ошибки совпадает с одной из условных веро-
ятностей р
ош
= р
1
= р
0
.
Условные вероятности ошибок находятся интегрированием условных
ФПВ откликов детекторов;
p(1/0) = ∫ W
0
(u)du
∞
U
0
; p(0/1) = ∫ W
1
(u)
U
0
−∞
du ,
где W
0
(u
) и W
1
(u) –
ФПВ откликов детекторов при условии формирования на
передаче 0 или 1 соответственно.
Оценим помехоустойчивость передачи двоичных символов при различ-
ных сигналах дискретной модуляции и различных методах их приема.
При передаче сигналов ДАМ (см. рис. 5,г) символ 0 соответствует от-
сутствию сигнала, а символ 1 – передаче сигнала с постоянной амплитудой.
При этом на выходе детектора ПРУ при передаче символа 0 напряжение будет
иметь ФПВ шума W
0
(u
), а при передаче 1 – ФПВ сигнала и шума W
1
(u
) в соот-
ветствии с рис. 7,а.
Когерентный прием (обработка) сигнала ДАМ (при φ
г
–
φ
0
= 0)
характе-
ризуется гауссовской ФПВ отклика детектора:
W
0
(u) =
1
√2πσ
ш
exp �−
u
2
2σ
ш
2
�, W
1
(u) =
1
√2πσ
ш
2
exp �−
(u−U
m
)
2
2σ
ш
2
�
Для симметричного ДКС выполняется равенство р(1/0) = р(0/1) = р
1
.
Это
достигается при пороге РУ U
0
= U
m
/2
. Подставляя (28) и значение U
0
в (27), по-
лучаем:
р
ошДАМкп
= р
1
= 1 −
1
√2π
∫
exp �−
u
2
2σ
ш
2
� du = 1 − Ф �
h
√2
� ,
U
m
/2
−∞
где Ф(·) – табулированная функция Лапласа (см. Приложение 4); h =
U
m
σ
ш
.
При некогерентном приеме сигнала ДАМ на выходе детектора сигнал
характеризуется рэлеевским и райсовским распределениями ФПВ вида:
W
0
(u) =
u
σ
ш
2
exp �−
u
2
2σ
ш
2
� ; W
1
(u) =
u
σ
ш
2
exp �
u
2
+U
m
2
2σ
ш
2
� ∙ J
0
�
u∙U
m
σ
ш
2
�.
Подставляя выражения (30) в (27), получаем:
p(1/0) = ∫
u
σ
ш
2
∞
U
0
exp �−
u
2
2σ
ш
2
� du; p(0/1) = ∫
u
σ
ш
2
exp �−
u
2
+U
m
2
2σ
ш
2
�
U
0
0
∙ J
0
�
u∙U
m
σ
ш
2
� du.
(28)
(30)
(27)
(29)
(31)

34
Здесь J
0
(
β) – функция Бесселя первого рода нулевого порядка [5].
Учитывая, что ДКС симметричный и выполняется равенство р(1/0) =
р(0/1) = р
1
при значении порога РУ U
0
= U
m
/2
, а также представив U
m
= √2σ
ш
h,
из (31) получим:
р
ошДАМнп
= р
1
= ∫
u
σ
ш
2
exp �− �
u
2
2σ
ш
2
+ h
2
��
σ
ш
h
0
∙ J
0
�
u∙h
σ
ш
� du.
Зависимость р
ош
от значения h
2
,
полученные путем решения уравнения
(32)
, представлена в табл. 4.
Таблица 4
р
ош
5·10
-1
2·10
-1
10
-1
5·10
-2
10
-2
5·10
-3
10
-3
5·10
-4
10
-4
h
2
0
2,82
5,37
7,77
13,8
16,4
22,9
26,7
33,2
Величину р
ош
для промежуточных значений h
2
можно найти методом экстрапо-
ляции.
При передаче сигналов ДЧМ (см. рис. 5,д) символ «0» соответствует пе-
редаче сигнала на частоте f
2
, а символ «1» - передаче сигнала на частоте f
1
. Из
рис. 7,б следует, что при передаче «0» через ППФ, настроенный на частоту f
2
,
будет проходить сигнал с несущей частотой f
2
и шум в полосе пропускания это-
го ППФ. Через ППФ, настроенный на частоту f
1
, при передаче нуля будет про-
ходить только шум в полосе пропускания этого ППФ. Аналогичный результат
получается при передаче символа «1».
Ошибочные решения здесь будут тогда, когда отклик детектора в кана-
ле, по которому сигнал не передается, превзойдет значение отклика детектора в
канале, по которому сигнал передается.
Для симметричного ДКС, с учетом приведенных выше замечаний, получаем:
р
ош
= р(0/1) = р(1/0) = � W
0
(x)W
1
(u)dxdu
∞
0
.
Подставляя функцию ФПВ из (28) или из (30) в (33) при когерентном приеме,
получим:
р
ошДЧМкп
= р
1
= 1 –
Ф(h).
При некогерентном приеме выражение для р
ош
имеет вид:
Р
ошДЧМнп
=
р
1
= 0,
5ехр{-h
2
/2}.
При передаче сигналов ДФМ [см. (19) и рис. 5,е] символ «0» соответ-
ствует передаче сигнала с начальной фазой -π/2 , а символ «1» – передаче сиг-
нала с начальной фазой +π/2. В этом случае отклик когерентного (фазового) де-
тектора будет иметь ФПВ вида (26). Выбрав фазу опорного напряжения равную
φ
г
= +
π/
2, получаем:
W
0
(u) =
1
√2πσ
ш
exp �−
(u+U
m
)
2
2σ
ш
2
�, W
1
(u) =
1
√2πσ
ш
2
exp �−
(u−U
m
)
2
2σ
ш
2
�.
Подставляя выражения (34) в (27) и выбирая U
0
= 0
для симметричного ДКС,
получаем:
Р
ошДФМ
=
р
1
=
1 − Ф�√2ℎ�.
(34)
(32)
(33)

35
Оценим помехоустойчивость передачи двоичных сигналов при относи-
тельной фазовой модуляции, когда прием производится по методу сравнения
фаз (СФ ) и по методу сравнения полярностей (СП).
Ошибочный прием двоичного символа при ДОФМ-СП возникает, когда
осуществляется одно из двух несовместных событий (см. рис. 7,г):
1) данный символ принят правильно, а предыдущий ошибочно;
2) данный элемент принят ошибочно, а предыдущий правильно.
Вероятность появления какого-либо из этих двух несовместных событий
есть р
ош
при ДОФМ-СП:
р
ошДОФМ-СП
= р
1
=2р
ошДФМ
(1 –
р
ошДФМ
) =
2Ф�√2h��1 − Ф�√2h��.
При приеме сигнала ДОФМ по методу сравнения фаз (см. рис. 7,в) имеем:
р
ошДОФМ-СФ
=
р
1
= 0,
5 ехр(-h
2
).
Скорость передачи информации по дискретному каналу связи R опреде-
ляют как количество взаимной информации I(у, х), передаваемой по ДКС в
единицу времени:
R =
1
τ
и
I(x, y) =
1
τ
и
�H
y
− H
y/x
�,
где для ДКС двоичные символы (нули и единицы) будут соответственно
х = {b
i
} –
на передаче, и ???????? = �????????�
????????
� – на приеме;
Н
y
–
энтропия принятой последовательности двоичных единиц:
H
y
= − ∑ p�b�
j
�log
2
p�b�
j
�
1
j=0
;
H
y/x
–
условная энтропия:
H
y/x
= − ∑ p(b
i
) ∑ p�b�
j
/b
i
�log
2
p�b�
j
/b
i
�
1
j=0
1
i=0
.
Для двоичного симметричного ДКС, когда
p�b�
0
= 0/b
1
= 1� = p
1
= p�b�
1
= 1/b
0
= 0�
и одинаковы априорные вероятности передачи р(0) = р(1), формула (35), с уче-
том (36) и (37) может быть представлена в виде:
R
2
=
1
τ
и
[1 + p
1
log
2
p
1
+ (1 − p
1
)log
2
(1 − p
1
)].
Так как вероятности ошибок р
ош
=
р
1
для различных видов сигналов за-
висят от отношения С/Ш h
2
на входе детектора, то R
2
также зависит от С/Ш.
Для сравнения скорости передачи информации R
2
=
Ψ(h
2
) при данном
виде модуляции и способе приема с пропускной способностью НКС (скоростью
передачи информации при идеальном кодировании и модуляции) С = Θ(h
2
) (23)
вводят показатель эффективности:
Э = R
2
/
С.
Эффективность системы передачи высока, если Э → 1 (R
2
→ С), и эффектив-
ность низка при Э → 0.
2.9. Анализ характеристик и параметров цифро-аналогового преобразо-
вания сообщения
Цифро-аналоговое преобразование (ЦАП) позволяет на приемном конце
системы связи восстановить непрерывное сообщение ĝ(t) по принятым кодовым
комбинациям b�
k
m
сигнала ИКМ. Это осуществляется с помощью следующих
(35)
(37)
(36)