Электронный вариант учебного пособия «Рентгенография металлов» содержит тот же материал, что и печатный учебник, но в некоторые формулировки и выражения были внесены изменения при позднем редактировании., За обнаруженную некоторую разницу в тексте, автор приносит извинения.

В.М.Ершов

Содержание

Введение	6
Основы физической кристаллографии	7
Кристаллическая решетка	7
Кристаллические системы	10
Элементарные ячейки	13
Кристаллографические символы узла, плоскости и направления в элементарной ячейке	15
Квадратичные формы для основных сингоний	21
Угол между двумя пересекающимися плоскостями	24
Физика рентгеновских лучей	26
Источники рентгеновских лучей	26
Измерение длины волны рентгеновских лучей	31
Сплошной (непрерывный) спектр рентгеновских лучей	35
Характеристический спектр рентгеновских лучей	38
Взаимодействие рентгеновских лучей с веществом	45
Фильтры рентгеновских излучений	51
Методы регистрации рентгеновских излучений	53
Теория интерференции рассеянных рентгеновских лучей	59
Рассеивание рентгеновских лучей атомным Рядом	60
Рассеивание рентгеновских лучей атомной плоскостью и кристаллом	63
Формула Вульфа-Брэггов	67
Рассеивание рентгеновских лучей поликристаллическими веществами	72
Интенсивность интерференционных линий рентгенограммы	76
Основные методы рентгеноструктурного анализа	86
Метод Лауэ	87
Метод вращающегося кристалла	94
Метод Дебая-Шерерра (метод порошка)	99
Подготовка образца к съемке	101
Выбор излучения и фильтров для рентгеновской съемки	103
Схемы съемки рентгенограмм	105
Расчет рентгенограммы порошка	110
Индицирование рентгенограммы	117
Точное измерение параметров кристаллической решетки	124
Рентгеновская дифрактометрия	129
Прикладной рентгеновский анализ	133
Рентгеновский анализ металлических твердых растворов	134
Рентгеновский метод определения типа твердого раствора	136
Рентгеновский анализ твердых растворов замещения	138
Построение кривой ограниченной растворимости компонентов на диаграмме состояния	142
Рентгеновский анализ неоднородных и упорядоченных твердых растворов	145
Рентгеновский анализ твердых растворов внедрения	147
Рентгеновский фазовый анализ сплавов	152
Качественный фазовый анализ	152
Количественный фазовый анализ	157
Рентгеновская тензометрия	165
Методика расчета напряжений первого рода	166
Метод расчета напряжений второго рода	176
Расчет напряжений третьего рода	184
Рентгеновский анализ текстур металлов	185
Рекомендуемая литература	204

---

ВВЕДЕНИЕ

В ноябре 1995 года все прогрессивное человечество отметило 100-летний юбилей одного из крупнейших событий в науке XIX века - открытия рентгеновских лучей.

Знаменитый немецкий физик Вильгельм Конрад Рентген обнаружил неизвестный ранее вид излучения, которое он назвал X-лучами. Под влиянием этих лучей, исходящих от анода катодной трубки, в темноте светился флуоресцирующий экран. Лучи действовали на фотографические пластинки и вызывали ионизацию газов. Они проходили сквозь непрозрачные для видимого света тела, поглощаясь тем менее, чем меньше была толщина этих тел и атомные номера элементов, входящих в их состав.

Первое практическое применение лучей, названных в честь ученого рентгеновскими, связано с областью медицинской диагностики, где большая проникающая способность излучения позволила обнаружить различные внутренние пороки органов человека, скрытые от глаза специалиста. В последующие годы просвечивание было применено и в технике для изучения внутренней дефектности отливок, поковок, сварных швов и других деталей машин и механизмов. Эта область использования рентгеновского излучения получила название – рентгеновская дефектоскопия.

Другой, ещё более важной областью применения рентгеновских лучей, стал анализ строения неорганических и органических веществ. После открытия в 1912 году Максом фон Лауэ дифракции рентгеновских лучей на природных кристаллах и последующего за этим открытием анализа спектрального состава излучения, выполненного Брэггами, возник рентгеноструктурный анализ – мощный инструмент изучения атомного строения твердых и жидких тел.

Одновременно с рентгеноструктурным возник и рентгеноспектральный анализ, позволяющий исследовать химический состав разнообразных веществ.

В последующие за открытием рентгеновских лучей годы интенсивно совершенствовались аппаратура их получения и регистрации, создавались новые методы анализа совершенных и несовершенных кристаллов, расширялись области практического использования рентгенографии.

В настоящем пособии, созданном на основе лекций для студентов специальности («Обработка металлов давлением»), изложены основы теории рентгеноструктурного анализа металлов и сплавов, рассмотрены вопросы использования методов рентгенографии для решения практических задач будущих инженеров – металлургов.

1. ОСНОВЫ ФИЗИЧЕСКОЙ КРИСТАЛЛОГРАФИИ

1.1 КРИСТАЛЛИЧЕСКАЯ РЕШЕТКА

Давно было доказано, что кристаллы представляют собой систему упорядоченно расположенных атомов или молекул. И поскольку периодичность внутреннего строения является основной отличительной характеристикой кристаллического вещества, уместно представить себе систему расположения атомов в виде некоторой объемной сетки, так называемой пространственной решетки или просто решетки, в которой любую из точек (узлов) окружает равное число таких же точек.

---

Рассмотрим вначале некоторый произвольный атомный ряд. Расположение атомов вдоль этого ряда периодически повторяется с равными интервалами (Рис.1.1,а) и схематически может быть

Рисунок 1.1 – Схема атомного ряда а), атомной плоскости б), трехмерного кристалла в).

изображено в виде точек, удаленных одна от другой на равные расстояния (например, ).

Расположение атомов на плоскости может быть представлено в виде двухмерной точечной сетки, в которой каждая точка обозначает атом или группу атомов (молекул) (Рис.1.1,б). Если вектор определяет направление и величину расстояния между соседними атомами в ряду Х (трансляционное расстояние или просто трансляцию), а вектор - трансляцию, в другом направлении - y, то результат сложения векторов , где u и v – целочисленные коэффициенты, описывает положение атома на плоскости (Рис.1.1,б). С одной стороны, векторы и можно выбрать так, пробы коэффициенты u и v были целочисленными для любого из атомов плоскости. С другой стороны, может быть удобнее определять векторы другим способом, например, под прямым углом друг к другу; в этом случае числа u и v могут оказаться дробными для некоторых точек плоской сетки.

Теперь рассмотрим трехмерную периодическую решетку; для её описания уже необходимы три вектора трансляций , , , причем не лежащие в одной плоскости. ( Рис.1.1,в). Любая точка в трехмерной пространственной узловой сетке может быть описана с помощью выражения:

, (1.1)

причем векторы , , , могут быть выбраны таким образом, чтобы коэффициенты u, v и w оказались целочисленными. Трансляция c как бы «надстраивает» атомную плоскость, описываемую векторами и , над аналогичной и параллельной плоскостью. Таким образом, кристаллическую трехмерную решетку можно представить как совокупность параллельных атомных плоскостей. Это представление имеет большое значение для понимания сущности законов рассеяния рентгеновских лучей кристаллами.

Узлы пространственной решетки кристалла имитируют позиции отдельных атомов в большинстве структур металлов и других элементов периодической системы. Но в сложных соединениях, имеющих сильные молекулярные связи, нужно учитывать факт образования решетки из молекул, как, например, кристаллическая решетка льда в узлах содержит молекулы воды H₂O.

2. КРИСТАЛЛИЧЕСКИЕ СИСТЕМЫ

В кристаллографии принято считать, что векторы трансляций играют для кристаллической структуры роль пространственных координат. В зависимости от природы рассматриваемого объекта эти оси кристалла могут быть как равной, так и совершенно различной длины, и направлены друг к другу под произвольными углами. Если перебрать все возможные варианты равенства и неравенства этих базисных трансляций и углов между ними, то обнаружится, что в природе возможно существование 14 различных типов пространственных решеток, которые называются решетками Бравэ. Каждый из 14 видов решеток носит название трансляционной группы. Рассмотрим особенности этих основных систем.

---

Прежде всего, нужно учесть то обстоятельство, что для описания положения узла в решетке или атома в кристаллической структуре, необходимо определить его координаты относительно осей кристалла. Наиболее симметричные кристаллы могут быть описаны с помощью трехосной прямоугольной системы координат, в которой оси соответствуют трем граням куба. Каждая из пространственных решеток характеризуется некоторой наиболее удобной для нее системой координат. В кристаллографии используется 7 различных систем координат, отличающихся друг от друга по величине осей и углов между ними. Эти 7 различных кристаллических систем носят название сингоний (табл.1.1) В кристаллографии обычно используется правосторонняя система координат; векторы , , , на рис.1.2 расположены согласно правилу правой руки. Угол, противолежащий вектору , обозначается как и т.д.

Рисунок 1.2 – Оси пространственной решетки, углы между осями; элементарная ячейка.

После того как кристаллическая структура будет определена, можно уже найти в элементарной ячейке величину трансляций a, b, c и углы между ними , и .

В таблице 1.1 представлены виды сингоний или кристаллических систем с некоторыми примерами принадлежащих им веществ.

Таблица 1.1 – Сингонии кристаллов

Система	Оси трансляции и углы между ними	Пример
Триклинная	Все трансляции не равны между собой и наклонены друг к другу под различными углами: ;	K2CrO7
Моноклинная	Три трансляции произвольной неравной длины, два угла из трех прямые: ;	CaSO4
Ромбическая (орторомбическая)	Три трансляции не равны между собой и наклонены друг к другу под прямым углом: ;	Ga
Тетрагональная	Все оси под прямым углом друг к другу, две из них равны: ;	TiO2
Кубическая	Три равные оси под прямым углом друг к другу: ;	Cu.Al
Гексагональная	Три равные оси в одной плоскости под углом 120° друг к другу, перпендикулярны четвертой произвольной длине: ; ;	Ti.Zn
Ромбоэдрическая (тригональная)	Три равные оси наклонены друг к другу под равными непрямыми углами: ;	As, Sb, Bi

3. ЭЛЕМЕНТАРНЫЕ ЯЧЕЙКИ

Векторы трансляций кристаллической решетки образуют ребра некоторого параллелепипеда, получившего название элементарной ячейки. Каждый кристалл сложен из периодически повторяющихся элементарных ячеек, одинаковых по размеру, форме и ориентировке. Элементарная ячейка является как бы основным строительным кирпичиком для всего кристалла. Расположение атомов в ячейке обычно изображается с помощью точек в вершинах пространственной решетки, однако возможно расположение атомов в центрах отдельных граней элементарной ячейки и в центре её объема. Элементарная ячейка, состоящая из атомов, расположенных только в узлах пространственной решетки, называется примитивной ячейкой. С её помощью в принципе можно изобразить все 14 видов решеток Бравэ (Рис. 1.3).

---

Сложные решетки характеризуют с помощью так называемого базиса. Базис пространственной решетки есть совокупность координат всех неидентичных атомов, находящихся в элементарной ячейке. Эти координаты выражаются в долях осевых трансляций. Число базисных атомов указывает, сколько атомов приходится на одну ячейку. Например, примитивная ячейка имеет один атом на элементарную ячейку, координаты которого будут 000; сложная объемноцентрированная ячейка имеет два атома на элементарную ячейку с координатами 000, ; сложная гранецентрированная ячейка имеет четыре атома на элементарную ячейку с координатами 000, , и .

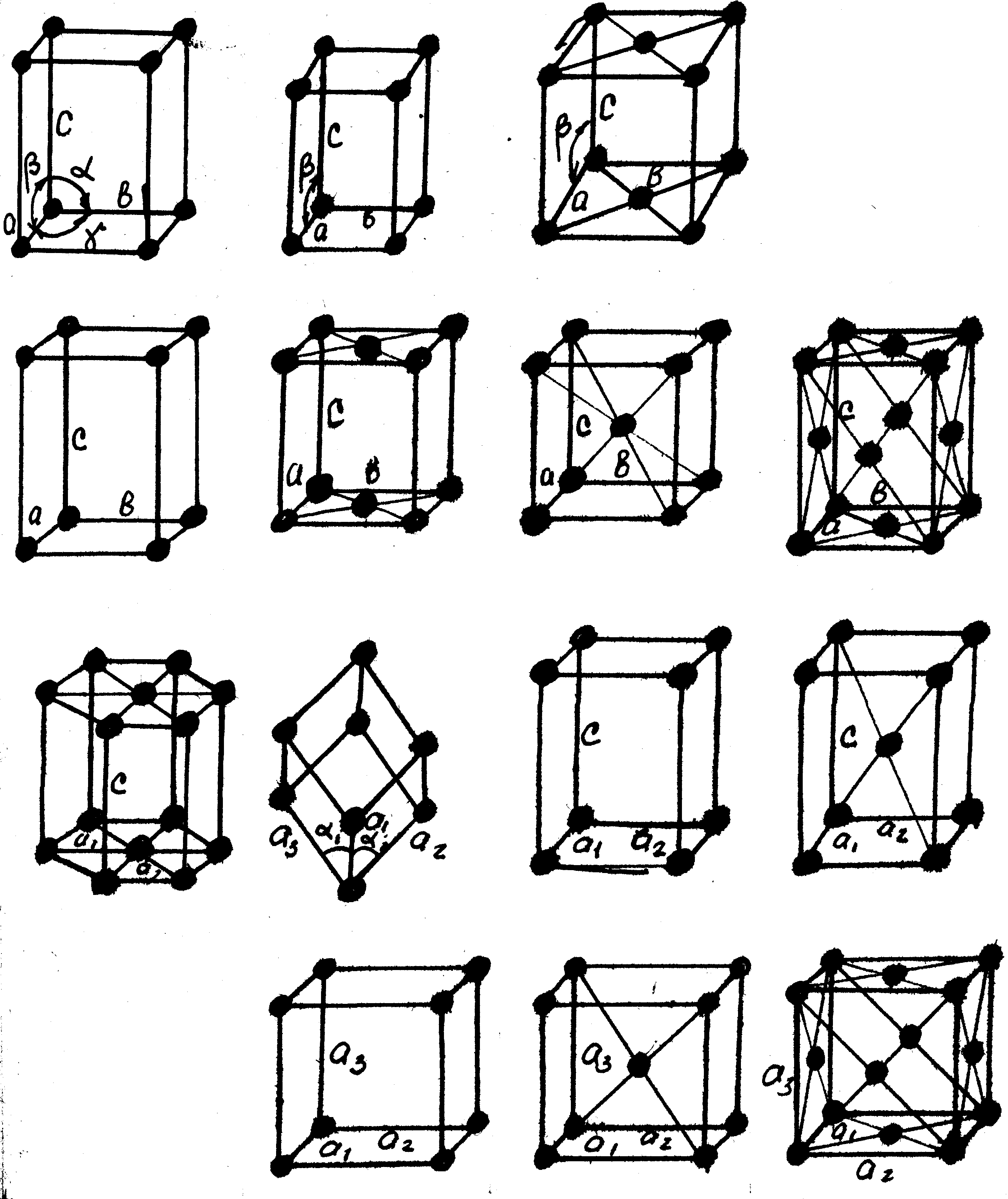
1 2 3

4 5 6 7

8 9 10 11

12 13 14

где 1 – триклинная примитивная; 2 – моноклинная примитивная; 3 – моноклинная базоцентрированная; 4 – ромбическая примитивная; 5 – ромбическая базоцентрированная; 6 – ромбическая объемноцентрированная; 7 – ромбическая гранецентрированная; 8 – гексагональная; 9 – ромбоэдрическая; 10 – тетрагональная примитивная; 11 – тетрагональная объемноцентрированная; 12 – 14 кубическая примитивная, объемноцентрированная и гранецентрированная.

Рисунок 1.3 – Типы пространственных решеток.

3. КРИСТАЛЛОГРАФИЧЕСКИЕ СИМВОЛЫ УЗЛА, ПЛОСКОСТИ И НАПРАВЛЕНИЯ В ЭЛЕМЕНТАРНОЙ ЯЧЕЙКЕ

Для обозначения узла в кристаллической решетке используется система символов из трех чисел, которые означают количество трансляций по осям системы координат, соответственно по X,Y и Z. На рис.1.4 показан пример обозначения символов узлов для кристаллической решетки.

Рисунок 1.4 – Символы узлов в объемноцентрированной решетке.

Символы заключаются в двойные квадратные скобки.

Символы атомной плоскости определяются по отрезкам, которые плоскость отсекает по осям системы координат. В отрезках А, В, С атомная плоскость будет обозначаться следующим видом: , где , и - осевые трансляции, или для симметричных атомных решеток - параметры или периоды решеток. Круглые скобки, в которые заключаются отношения, обозначают указание на то, что речь идет об атомной плоскости. Таким образом, в отрезках плоскость характеризуется дробными символами, что весьма неудобно. Но если обозначить эти отношения: и взять обратные величины этих символов, то получим так называемые индексы Миллера: . Так, если , то есть отрезок А, который отсекает плоскость по оси Х, будет составлять половину параметра решетки ; , то есть, соответственно, параметра ; р=1, то есть отрезок С равен параметру решетки по оси Z – C, получим:

тогда плоскость с индексами h=2, k=3 и l=1 будет обозначаться как (231) и читаться два, три, один. Данная плоскость представлена на рис. 1.5.

Рисунок 1.5 – Обозначение атомной плоскости в элементарной ячейке.

---

Смотрите также файлы

• Sotsiologia_kak_nauka.doc

• Метод.указ.по выпол.курс.работ.doc

• жел.дис.мет.doc

• ИТ LAB ORG & MANAG 2011.doc

• Гепатиты.Циррозы. Метод.рек.2010.doc