Файл: Лабораторная работа 23. Статистические функции Excel. Метод экспертных оценок. Цель работы.doc

Лабораторная работа №23. Статистические функции Excel. Метод экспертных оценок.

Цель работы: научиться прогнозировать спрос товаров, используя статистические функции Excel, а также использовать метод предпочтений при определении степени влияния различных факторов на эффективность производства.

Задачи:

1. 
   Прогноз спроса товаров.
   
2. 
   Метод экспертных оценок.
   

Задание №1. Прогноз спроса товаров, исходя из данных предыдущих периодов.

Предполагается, что имеются данные о покупке товаров за 2002, 2003 и 2004 годы. Необходимо спрогнозировать объем покупок на 2005 год.

Задание решается двумя способами:

1. 
   алгоритмическим способом, т.е. способом пошаговой экстраполяции;
   
2. 
   функциональным способом с использованием функций ТЕНДЕНЦИЯ и РОСТ.
   

Функция ТЕНДЕНЦИЯ аппроксимирует исходные данные по прямой, а функция РОСТ – по экспоненциальной кривой. Все данные, прогнозируемые алгоритмическим и функциональным способами, отобразите на графике.

Выполнение работы:

1. 
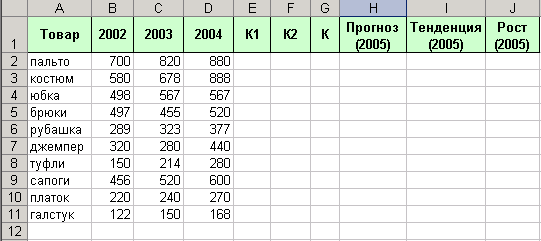
   В MS Excel создайте таблицу следующего вида и сохраните в папке с номером вашей группы под именем Прогноз.
   

2. 
   Отформатируйте таблицу: для шапки таблицы установите полужирный шрифт, выравнивание по центру, светло-зеленый цвет фона, обрамление – все границы.
   
3. 
   В таблицу введите исходные данные о покупке товаров (не менее 10 наименований) за 2002, 2003 и 2004 годы.
   
4. 
   Определите коэффициенты:
   

К1=(2003-2002)/2002;

К2=(2004-2003)/2003.

5. 
   Определите средний коэффициент:
   

К=(К1 + К2)/2

6. 
   Рассчитайте прогноз на 2005 год:
   

П=2004+2004*К

7. 
   Рассчитайте прогноз объема покупок функциональным способом. С помощью мастера вызовите функции ТЕНДЕНЦИЯ и РОСТ (категория Статистические).
   

ТЕНДЕНЦИЯ (ВХ:ВХ;;4),

РОСТ (ВХ:ВХ;;4), где ВХ:ВХ – диапазон исходных данных.

8. 
   Данные, прогнозируемые алгоритмическим и функциональным способами, отобразите на графике. Используйте тип диаграммы График, вид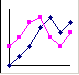 . Дайте диаграмме заголовок – Прогноз спроса товаров, оси Х – Товар, оси Y – Прогноз.
   
9. 
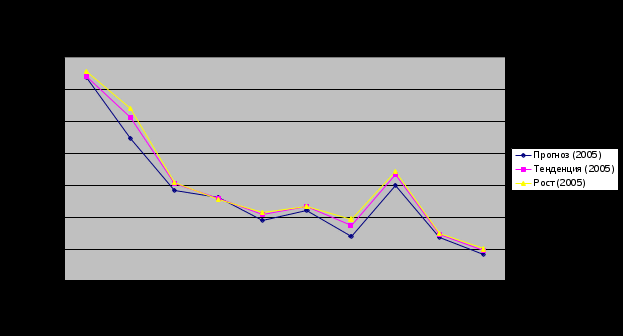
   Диаграмма должна иметь приблизительно следующий вид:
   

---

10. 
    Проанализируйте полученные результаты.
    

Задание №2. Определение степени влияния различных факторов на эффективность производства с использованием метода предпочтений.

В ходе разработки плана мероприятий по повышению эффективности производства (в частности, по повышению производительности труда) возникает задача определения степени влияния различных факторов на эффективность производства.

Для решения таких задач предлагается использовать метод экспертных оценок. Этот метод применяется для решения задач, которые невозможно описать в виде каких-либо математических соотношений, например, в виде системы уравнений. Такие задачи называются неструктурированными.

В нашем случае будет использован один из методов экспертных оценок, а именно, метод предпочтений, суть которого описана далее.

Например, пусть требуется оценить влияние на рост производительности труда следующих факторов:

1) уровень профессиональной подготовки рабочих;

2) соблюдение технологической дисциплины;

3) эффективность материальных стимулов;

4) эффективность организации соревнования;

5) технологическое переоснащение.

В качестве экспертов, оценивающих влияние этих факторов на рост производительности труда, выступают следующие специалисты предприятия:

1) главный инженер;

2) главный экономист;

3) начальник ОТиЗ;

4) начальник одного из цехов.

Обозначим количество экспертов через m (m = 4).

Количество оцениваемых факторов через n (n = 5).
Выполнение работы:

1. 
   В MS Excel Создайте таблицу следующего вида (исходную матрицу оценок) и сохраните ее в своей папке под именем Метод предпочтения:
   

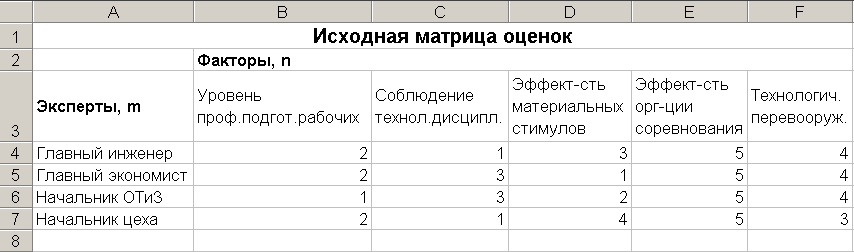
Здесь, например, первый эксперт (главный инженер) считает, что наибольшее влияние на рост производительности труда может оказать соблюдение технологической дисциплины

---

, следующий по важности фактор - уровень профессиональной подготовки рабочих, и т.д.

2. 
   Отформатируйте таблицу по образцу: для ячеек A1:F1 и B2:F2 установите объединение, заголовок таблицы отцентрируйте и задайте для него полужирный шрифт размером 12. Ячейки A3:F3 отцентрируйте по вертикали.
   
3. 
   Присвойте Листу имя Исходная матрица.
   
4. 
   Далее произведите преобразование матрицы оценок по формуле:
   

A_ji= n - x_ji, где j = 1...m; i = 1...n.

Например, A₁₂ = 5-x₁₂ = 5-1= 4. Для этого:

• 
  Перейдите на новый лист и присвойте ему имя Преобразование.
  
• 
  Скопируйте исходную матрицу на новый лист.
  
• 
  Сделайте преобразование по приведенной выше формуле. В результате должна быть получена следующая матрица:
  

5. 
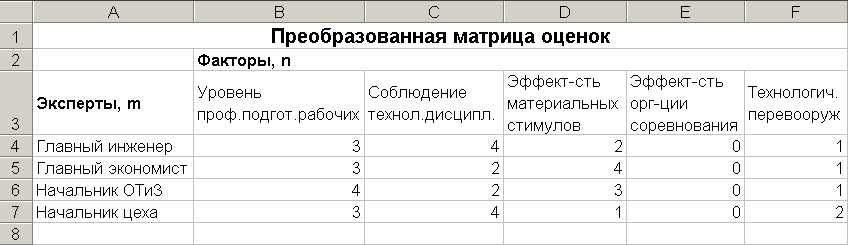
   Добавьте в таблицу следующие сведения:
   

6. 
   Далее найдите суммы преобразованных оценок по каждому из факторов:
   

_m

С_i =  A<sub>ji

j=1</sub>

7. 
   Найдите сумму всех оценок С по формуле:
   

_n

С =  С<sub>i.

i=1</sub>

8. 
   Найдите веса факторов Vi по формуле:
   

Vi = Ci/C

9. 
   Убедитесь, что полученные данные совпадают с данными, приведенными ниже:
   

Самым важным, по мнению экспертов, является фактор, имеющий максимальный вес. В данном случае, это уровень профессиональной подготовки рабочих. Следующий по важности - фактор, имеющий следующий по величине вес. В данном случае, это соблюдение технологической дисциплины, и т. д.

Требуется также проверить, насколько согласованными были мнения экспертов. Если мнения экспертов резко различаются, то, возможно, требуется повторить их опрос и уточнить некоторые оценки.

Для проверки согласованности мнений экспертов вычисляется величина, называемая коэффициентом конкордации W. Вычислим коэффициент конкордации W.

10. 
    Перейдите на лист Исходная матрица и добавьте следующие сведения:
    

---

11. 
    Найдите сумму оценок, указанных экспертами по каждому из факторов по формуле
    

_m

S_i =  x<sub>ji

j=1</sub>

12. 
    Найдите вспомогательную величину А по формуле:
    

A = m(n+1)/2

13. 
    Найдите разность Ri по формуле:
    

Ri = Si - A

14. 
    Найдите сумму квадратов разностей:
    

_{n 2}

S =  Ri

_i=1

Используйте математическую функцию СУММКВ.

15. 
    Найдите коэффициент конкордации W по формуле:
    

12S

W = --------------------

m² n(n²-1)

16. 
    Убедитесь, что получены следующие результаты:
    

17. 
    Сделайте анализ степени согласованности следующим образом. Коэффициент конкордации W изменяется от 0 до 1, причем его равенство 1 означает, что все эксперты дали одинаковые оценки по данному признаку Х, а равенство 0 означает, что связи между оценками, полученными от разных экспертов, не существует. При W > 0,5 степень согласованности экспертных оценок может считаться достаточной. При W < 0,5 требуется уточнение экспертных оценок. В данном примере W = 0,7375 , значит, уточнения оценок не требуется.
    

Задание №3.

Возьмите в качестве исходной матрицы оценок одну из ниже приведенных из вариантов значений матриц оценок. Причем, значения оценок 4-ого эксперта проставьте по своему усмотрению. Решите задачу с применением метода предпочтения для получившейся исходной матрицы оценок.

Если в результате выполнения задания получится значение коэффициента конкордации W> 0,5, то задачу можно считать решенной, а если в результате выполнения задания получится значение коэффициента конкордации W< 0,5, это означает, что требуется уточнение экспертных оценок. В этом случае изменяйте значения 4-ого эксперта до тех пор, пока не получится значение коэффициента конкордации W> 0,5.

Варианты значений матрицы оценок.

Вариант № 1.

	Факторы
Эксперты	1	2	3	4	5
1	2	1	3	5	4
2	2	3	1	5	4
3	1	3	2	5	4
4

---

Вариант № 2.

	Факторы
Эксперты	1	2	3	4	5
1	4	1	5	2	3
2	2	3	4	5	1
3	2	3	5	1	4
4

Вариант № 3.

	Факторы
Эксперты	1	2	3	4	5
1	1	4	5	2	3
2	2	3	4	5	1
3	1	4	5	3	2
4

Вариант № 4.

	Факторы
Эксперты	1	2	3	4	5
1	2	5	3	2	4
2	2	3	1	5	3
3	1	5	2	3	4
4

---