Файл: Реферат Давление газа с точки зрения молекулярнокинетической теории. Уравнение состояния идеального газа..docx
Добавлен: 12.01.2024
Просмотров: 131
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
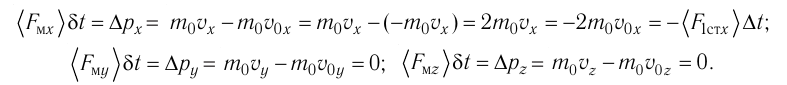
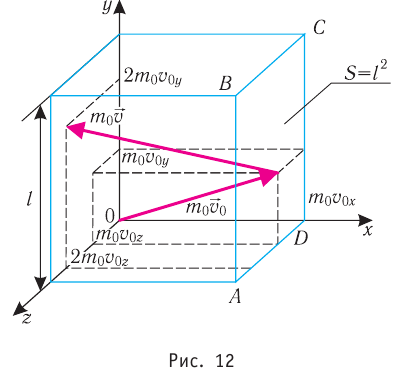
Так как промежуток времени между двумя последовательными соударениями молекулы со стенкой ABCD
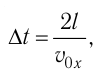 то
то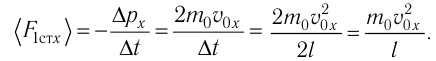
Проекция полной средней силы, с которой все N молекул, находящиеся в сосуде, действуют на стенку ABCD
Следовательно,
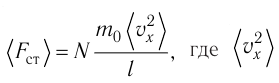 — усреднённый но всем N частицам квадрат проекций их скоростей на ось Ох.
— усреднённый но всем N частицам квадрат проекций их скоростей на ось Ох.Разделив обе части соотношения для
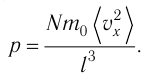
Так как
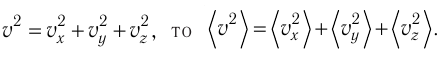 Поскольку молекулы газа совершенно одинаково отражаются от трёх пар противоположно расположенных граней куба, то
Поскольку молекулы газа совершенно одинаково отражаются от трёх пар противоположно расположенных граней куба, то 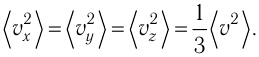 С учётом того, что занимаемый газом объём
С учётом того, что занимаемый газом объём 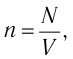 получим:
получим: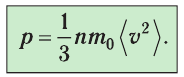 (3.2)
(3.2)Уравнение (3.2) называют основным уравнением молекулярно-кинетической теории идеального газа. Это уравнение позволяет рассчитать макроскопический параметр
давление р газа через концентрацию п молекул, массу т0 молекулы и среднюю квадратичную скорость её теплового движения, определяемую по формуле
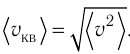 Иначе говоря, формула (3.2) связывает между собой макро- и микроскопические параметры системы «идеальный газ».
Иначе говоря, формула (3.2) связывает между собой макро- и микроскопические параметры системы «идеальный газ».Зависимость давления газа от среднего квадрата скорости движения его молекул объясняется тем, что с увеличением скорости, во-первых, возрастает импульс молекулы, а следовательно, и сила удара о стенку. Во-вторых, возрастает число ударов, так как молекулы чаще соударяются со стенками.
Обозначим через
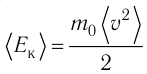 среднюю кинетическую энергию поступательного движения молекул. Тогда основное уравнение молекулярно-кинетической теории примет следующий вид:
среднюю кинетическую энергию поступательного движения молекул. Тогда основное уравнение молекулярно-кинетической теории примет следующий вид: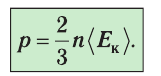 (3.3)
(3.3)Из выражения (3.3) видно, что давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации.
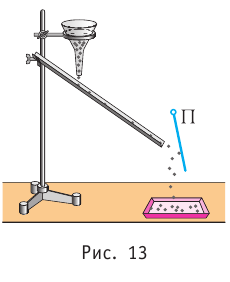
Проиллюстрировать зависимость давления от скорости движения молекул газа можно, используя механическую модель. Соберём установку, изображённую на рисунке 13. Закрепим пластину П таким образом, чтобы она могла поворачиваться вокруг горизонтальной оси. Насыплем в воронку с узким горлышком мелкую дробь. Используя наклонный жёлоб, направим на пластину струйку дроби (дробинки играют роль молекул). В результате многочисленных ударов дробинок пластина отклонится на некоторый угол под действием силы давления дробинок. Увеличив высоту, с которой скатываются дробинки, а следовательно, и их скорость в момент удара о пластину, можно заметить, что пластина отклонилась на больший угол. Отсюда можно сделать вывод: чем больше скорость движения дробинок, тем больше производимое на пластину давление.
1. Идеальный газ — модель газа, удовлетворяющая следующим условиям: 1 ) молекулы газа можно считать материальными точками, которые хаотически движутся; 2) силы взаимодействия между молекулами идеального газа практически отсутствуют (потенциальная энергия взаимодействия равна нулю); они
действуют только при столкновениях молекул, причём это силы отталкивания.
2. Уравнение, связывающее микронараметры состояния идеального газа (массу молекулы и её среднюю квадратичную скорость
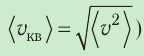 с его макропараметром (давлением, характеризующим газ как целое), непосредственно измеряемым на опыте, называют основным уравнением молекулярно-кинетической теории идеального газа:
с его макропараметром (давлением, характеризующим газ как целое), непосредственно измеряемым на опыте, называют основным уравнением молекулярно-кинетической теории идеального газа: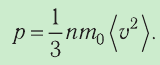
-
Давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации: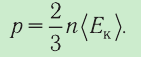
Уравнение состояния идеального газа
Уравнение состояния – устанавливает связь между параметрами состояния. В простейшем случае равновесное состояние тела определяется P, V, T. Связь между ними аналитически можно выразить так:
F(P, V, T) = 0
где F – некоторая функция параметров.
Это - уравнение состояния газа.
При обычных условиях параметры состояния многих газов хорошо описываются уравнением
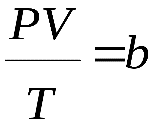
где b – константа, пропорциональная массе газа.
Это уравнение выполняется точно для идеального газа.
Идеальный газ – газ, молекулы которого не взаимодействуют друг с другом и имеют пренебрежимо малый объём. Молекулы соударяются друг с другом абсолютно упруго.
Если ввести молярный объём
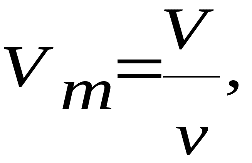 где ν – количество вещества и учесть, что
где ν – количество вещества и учесть, чтоm = m0NAν =µν
где m0 – масса одной молекулы.
µ - молекулярная масса.
NA – число Авогадро,
то уравнение состояния можно записать в виде
р Vm ν = b · T или PVm = RT *
Согласно закону Авогадро при одинаковых давлениях и температурах молярные объёмы Vm различных газов одинаковы. (Vm = 22.4·10-3м3) при Н.У.
Из этого закона и уравнения * следует, что постоянная R одинакова для всех газов. Это - универсальная газовая постоянная R = 8.31 Дж/(моль۰К)
Для произвольной массы газа
* *
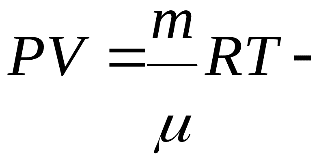 уравнение Менделеева Клапейрона,
уравнение Менделеева Клапейрона,т.к. R = kNA , где k – постоянная Больцмана
k = 1.38 · 10-23 Дж/К из ** получаем
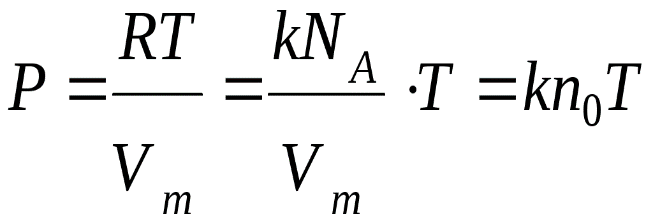
Р = kn0T
Ссылки на источники
-
Молекулярно-кинетическая теория URL https://www.evkova.org/molekulyarno-kineticheskaya-teoriya#Основное%20уравнение%20молекулярно-кинетической%20теории%20идеального%20газа -
Давление газа с точки зрения молекулярно-кинетической теории URL https://studfile.net/preview/7195848/page:17/ -
Уравнение состояния идеального газа URL https://studfile.net/preview/7195848/page:17/