Файл: метод МЭТ 12345 раб.doc

вольфрамовые α_l = (35-42)·10^-7 град^-1

Название этих стёкол определяется не их составом, а только тем, что коэффи-циенты α_l этих стёкол близки к значениям платины, молибдена, вольфрама.

Платиновые стёкла – это С90-1, С89-1, С89-6 (известково-магнезиаль-ные-баритовые) и свинцовые С87-1. Основой их является сплав системы SiO₂ - CaO - Na₂O. Для улучшения технологических и электрических свойств этого сплава вводится некоторое количество окиси бария, а окись натрия час-тично заменяется окисью калия.

Физико-химической основой стёкол является сплав системы SiO₂ - PbO - K₂O - Na₂O. В нём окись кальция исключена и заменена окисью свинца, а щелочной компонент содержит окислы калия и натрия с преобладанием Оки-си калия. Наиболее распространённое стекло этой системы С87-1 содержит в своём составе 55% SiO₂, 30% PbO, 9.2% K₂O, 3.8% Na₂O, 2% Al₂O₃.

Молибденовые стёкла – С47-1, С48-1, С49-2 и др. По химическому со-ставу это боросиликатные стёкла с высоким содержанием суммы окислов SiO₂ + B₂O₃ (85-90%) при относительно небольшом количестве щелочных окислов не более 0.5% при полном отсутствии окислов CaO, MgO. Окислы

SiO₂, B₂O₃ сближают коэффициенты расширения стеклоизделия с коэффи-циентами расширения молибдена и ковара, с которыми спаиваются эти стёк-ла.

Вольфрамовые стёкла – С38-1, С39-2, С40-1 также на основе SiO₂ + B₂O₃ 90%. Эти стёкла аналогичны по составу молибденовым стёклам, но с более высоким содержанием суммы окислов SiO₂ + B₂O₃ > 90% и меньшим содержанием щелочных окислов.

Термические свойства стёкол и измерение ктр

При оценке пригодности стёкол для применения в электронной про-мышленности решающими часто являются: термическое расширение, термо-стойкость, зависимость вязкости стекла от температуры.

Роль термического расширения для стёкол более существенна, чем для других материалов, т.к. механические напряжения, возникающие при нагре-вании или охлаждении стекла, бывают часто так велики, что превышают их прочность и вызывают разрушение стеклоизделий. Аналогичные явления могут происходить при спаивании двух стёкол с разными коэффициентами термического расширения.

Тепловое расширение обычно характеризуется коэффициентом терми-ческого расширения КТР (α_l). Численная величина α_l имеет значение для оп-ределения термостойкости стёкол, для оценки пригодности отдельных видов стёкол к спаиванию друг с другом или иными материалами, а также для тех-нического контроля при поставках.

Таким образом, коэффициент термического расширения (к.т.р.) являет-ся важнейшим технологическим параметром электровакуумных стёкол, опре-деляющим возможность соединения их с другими и образование спаев с ме-таллами.

Действующие стандарты требуют определения к.т.р. с точностью (1-2)·10^-7 K^-1, при абсолютных величинах (40-100)·10^-7 K^-1. Существующие кон-струкции дилатометров [1], обеспечивающие указанную точность измерения, неудобны в эксплуатации, т.к. имеют сложное отсчётное устройство (микро-скоп, оптический рычаг и т.д.).

Схема измерительной установки (дилатометр) представлена на рис.1. Испытуемый образец – стеклянный штабик или трубочка (1) диаметром до 5 мм помещается в печь (2). Конструкция печи обеспечивает равномерный на-грев участка образца длиной L = 160 мм. Регулирование температуры печи в пределах 20-600 ºС осуществляется изменением напряжения посредством автотрансформатора.

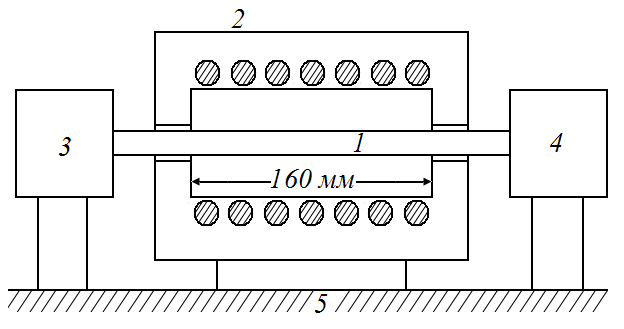
Рис.1. Схема конструкции дилатометра

Температура в печи измеряется термопарой типа ХК (хромель - копель) и ре-гистрируется пирометрическим милливольтметром. Одним концом образец упирается в стержень измерительного микрометра (3), другим в микрометри-ческий винт (4), который служит для балансировки системы. Указанные эле-менты конструкции смонтированы на массивной плите (5).

Зависимость Δl = f(ΔT) снимается при плавном увеличении температу-ры со скоростью не более 5 град/сек, которая обусловлена требованиями рав-номерного разогрева образца, в диапазоне температур 20…250 ºС. По данной зависимости Δl = f(ΔT) строится кривая теплового расширения стекла

из которой коэффициент термического расширения определяется как

L = 160 мм

Содержание отчёта

1. Цель работы

2. Основные теоретические положения

3. Схема установки

4. Описание эксперимента

5. Зависимость

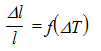
и расчёт КТР одного или двух типов стёкол

6. Выводы (к какой группе стёкол относится измеренный образец)

ЛИТЕРАТУРА

1. В. Эспе. Технология электровакуумных материалов. Т. 2, Энергия, 1968.

2. Пасынков В. В., Сорокин В. С. Материалы электронной техники. Высшая школа, 1986.

СЕВЕРО-КАВКАЗСКИЙ ОРДЕНА ДРУЖБЫ НАРОДОВ ГОРНО-

МЕТАЛЛУРГИЧЕСКИЙ ИНСТИТУТ

Кафедра электронные приборы

Лаборатория материалов электронной техники

ЛАБОРАТОРНАЯ РАБОТА № 3

ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА ПРОВОДНИКОВЫХ МАТЕРИАЛОВ

ВЛАДИКАВКАЗ

ЦЕЛЬ РАБОТЫ: ознакомление с методом измерения удельного сопро-

тивления металлов и сплавов

1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

Важнейшими применяемыми в электротехнике и электронике твёрдыми проводниковыми материалами являются металлы и их сплавы. Металличе-ские проводниковые материалы делятся на металлы высокой проводимости, имеющие удельное сопротивление ρ при нормальной температуре не более 0.1 мкОм·м, и сплавы высокого сопротивления с ρ при нормальной темпера-туре не менее 0.3 мкОм·м. Металлы высокой проводимости используют для изготовления проводов, токопроводящих жил кабелей, обмоток электриче-ских машин и трансформаторов и т.д. Сплавы высокого сопротивления при-меняют при изготовлении резисторов, электронагревательных элементов и т.д.

В металлах как в твёрдом, так и в жидком состояниях имеется весьма большое количество свободных электронов (электронов проводимости), ко-торые являются носителями заряда при прохождении через металл электри-ческого тока.

Согласно классической электронной теории металлов твёрдый про-водник представляют в виде системы из узлов кристаллической ионной ре-шётки внутри которой находится «электронный» газ, состоящий из коллекти-визированных (свободных) электронов. В коллективизированное состояние от каждого атома отделяются от одного до двух электронов. Ранее к электронному газу применялись и законы статистики обычных газов, что по-зволило математически вывести и объяснить найденные экспериментальным путём основные законы электропроводности (закон Ома) и потерь электриче-ской энергии (закон Джоуля – Ленца).

Хотя ряд вопросов удачно решён с помощью классической электронной теории металлов, обнаружились противоречия с опытными данными. Несо-ответствие теоретических и экспериментальных данных удалось преодолеть благодаря квантовой механике, согласно которой газ в металлах при обыч-ных температурах находится в состоянии «вырождения». В этом состоянии энергия газа почти не изменяется при изменении температуры. В состояние, аналогичное обычным газам, электронный газ приходит лишь при температу-рах, порядка тысяч Кельвин.

Особенности энергетического состояния твёрдого вещества описывает современная зонная теория. На рис.1 показаны энергетические диаграммы диэлектриков (а), полупроводников (б), проводников (в).

У проводящих материалов заполненная электронами зона вплотную прилегает к зоне свободных энергетических уровней и даже перекрывается ею. Вследствие этого электроны в металле свободны, т.к. они могут перехо-дить с уровней заполненной зоны на незанятые уровни свободной зоны под влиянием малейших возбуждений атомов. Энергию, необходимую для пере-вода электрона в свободное состояние, могут доставить не только тепловое движение, но и свет, поток электронов и ядерных частиц, электрические и магнитные поля и т.д.

Важным параметром, характеризующим свойства проводниковых мате-риалов, является удельная проводимость γ и её обратная величина – удель-ное сопротивление ρ.

Связь плотности тока J (А/м²), и напряжённости электрического поля E (В/м), в проводнике даётся известной формулой

J = γ · E (γ = e · n · μ) (1)

γ – удельная проводимость, (СМ/м).

Величина ρ = 1/γ – удельное сопротивление. Для имеющегося сопро-тивления R (Ом) проводника длиной l (м) и поперечным сечением S (м²) вычисляется по формуле

Единица СИ удельного сопротивления Ом·м.

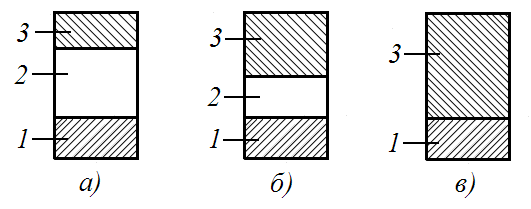
Рис.1. Энергетические зоны твёрдых тел:

а) диэлектрика

б) полупроводника

в) металла

1 – заполненная зона

2 – запрещённая зона

3 – свободная зона.

1 Ом·м = 10⁶ мкОм·м

Значения ρ некоторых материалов приведены в таблице № 1.

Согласно классической теории металлов удельная проводимость может быть вычислена следующим образом:

где e – заряд электрона

n₀ – число свободных электронов в единице объёма металла;

l_ср – средняя длина свободного пробега электрона между соударениями

между узлами решётки;

m – масса электрона;

V_т – средняя длина свободного пробега электрона в металле.

Для различных металлов скорости хаотического теплового движения электронов (при определённой температуре) примерно одинаковы. Незначи-тельно различаются и концентрации свободных электронов n₀. Например, концентрация электронов проводимости в серебре составляет 5.9·10²⁸ м^-3, в меди 8.5·10²⁸ м^-3. Поэтому значение удельной проводимости γ (или удельного сопротивления ρ) в основном зависит от средней длины свободного пробега в данном проводнике l, которая, в свою очередь, определяется структурой проводникового материала. Вследствие усиления колебаний узлов кристал-лической решётки появляется всё больше препятствий на пути направленно-го движения электронов, уменьшается средняя длина пробега и подвижность электронов снижается. Поэтому удельное сопротивление металлов с повыше-нием температуры возрастает.