Файл: Учебник для вузов. М Издво мгту им. Баумана, 2002, 336 с. Теоретические основы сапр Учебник для вузов Корячко В. П., Корейчик В. М., Норенков И. П. М. Энергоатомиздат, 1987, 400 с.doc

Информационное – всевозможные данные для АП. Основная составная часть ИО – банк данных (совокупность средств для централизованного накопления и коллективного использования данных в САПР). Банк данных состоит из базы данных и системы управления базой данных.

База данных – сами данные, находящиеся в памяти ЭВМ и каким-либо образом структурированные.

Система управления базой данных – совокупность программных средств, которые обеспечивают работу банка данных (запись данных, их выборка по запросам пользователей и прикладных программ, защита данных от искажений и несанкционированного доступа).

Лингвистическое – совокупность языков, применяемых для описания проектных процедур и решений.

Методическое – документы, характеризующие состав, правила отбора и эксплуатации средств АП.

Организационное – положения, инструкции, приказы, квалификационные требования и др. документы, которые регламентируют работу проектной организации и ее взаимодействие с САПР.

Краевые задачи при проектировании технических объектов

Проектирование многих технических объектов связано с необходимостью анализа непрерывных физических процессов, математическим описанием которых являются дифференциальные уравнения в частных производных (переходные процессы в СЭ, уравнения Навье-Стокса для описания течения газов с учетом вязкости воздуха). Эти уравнения как правило имеют множество решений. Для получения единственного решения необходимо задать краевые условия. Это – сведения об искомых непрерывных функциях на границах рассматриваемых областей – граничные условия, а в случае нестационарных задач (есть изменения значений функции во времени) – значения этих же функций в начальный момент времени – начальные условия. Исходное дифференциальное уравнение в частных производных вместе с краевыми условиями называется дифференциальной краевой задачей и представляет собой ММ исследуемого объекта.

Граничные условия в краевых задачах могут задаваться различными способами.

На границе рассматриваемой области можно задать:

– значение искомой функции;

– значения производных по пространственным координатам от искомой функции. Например, при использовании модуля PDEtool ППП Matlab для моделирования процессов обтекания какого-либо тела двухмерным плоскопараллельным потоком невязкого газа задаются граничные условия непротекания потока через стенки тела, т.е. скорость на границе = нулю.

---

Точное решение краевых задач удается получить лишь для немногих частных случаев. Поэтому общий способ их решения, в том числе и в САПР, заключается в использовании различных приближенных моделей. Наиболее широкое распространение получили модели на основе интегральных уравнений и модели на основе метода сеток.

Основная идея построения модели на основе интегральных уравнений заключается в переходе от исходного диф.уравнения в частных производных к эквивалентному интегральному уравнению, подлежащему дальнейшим преобразованиям.

Сущность метода сеток состоит в аппроксимации искомой непрерывной функции совокупностью приближенных значений, рассчитанных в некоторых точках – узлах. Совокупность узлов, соединенных определенным образом, образует сетку. Сетка, в свою очередь, является дискретной моделью области определения искомой функции.

Применение метода сеток позволяет свести дифференциальную краевую задачу к системе нелинейных в общем случае алгебраических уравнений относительно неизвестных узловых значений функций.

В общем случае алгоритм метода сеток состоит из трех этапов.

1. Построение сетки в заданной области (дискретизация задачи).

2. Получение системы алгебраических уравнений относительно узловых значений (алгебраизация задачи).

3. Решение полученной системы алгебраических уравнений.

Наиболее часто в составе САПР используются два метода сеток: метод конечных элементов (МКЭ) и метод конечных разностей (МКР). Эти методы отличаются друг от друга на 1 и 2 этапах алгоритма. На 3 – практически идентичны.
Метод конечных элементов

Начал развиваться как метод решения задач строительной механики. Сейчас: авиация, космос, расчет электродвигателей (ППП COSMOS/M в составе ProEngeniering, Matlab, Phoenics и др.). Основные преимущества: доступность и простота понимания, применимость для задач с произвольной формой области решения, возможность создания на основе метода высококачественных универсальных программ для ЭВМ.

В МКЭ исходная область определения функции разбивается с помощью сетки, в общем случае неравномерной, на отдельные подобласти – конечные элементы. Искомая непрерывная функция аппроксимируется кусочно-непрерывной, определенной на множестве конечных элементов. Аппроксимация может задаваться произвольным образом, но чаще всего для этих целей используются полиномы, которые подбираются так, чтобы обеспечить непрерывность искомой функции в узлах на границах элементов.

---

Система конечно-элементного моделирования T-FLEX Анализ

Порядок работы расчетчика.

1. Построение трехмерной модели.

2
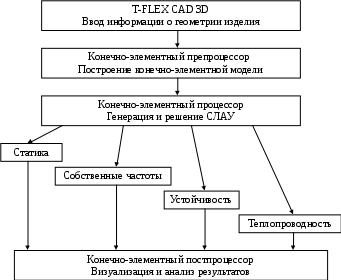
. Генерация сеточной конечно-элементной модели изделия с помощью препроцессора: создание конечно-элементной сетки, отражающей геометрию изделия и наложения граничных условий, определяющих физическую задачу, подлежащую решению.

Объемная постановка: тетраэдральные конечные элементы двух типов – четырехузловые и десятиузловые. Элементы первого типа обеспечивают линейную аппроксимацию искомой функции (например, перемещений или температуры) в пределах объема КЭ – для быстрой качественной оценки.

Элементы второго типа, десятиузловые, обеспечивают более высокий порядок аппроксимации – квадратичную аппроксимацию, и лучше аппроксимируют криволинейные границы – для ответственного количественного анализа.





Настройки генератора сеток позволяют создавать адаптивные сетки с переменным шагом. Такие сетки имеют сгущения конечных элементов в местах модели со сложной геометрией, в которых можно ожидать концентрации напряжений.

Кроме построения КЭ-сетки, с помощью препроцессора задаются граничные условия. Для этого предусмотрены специальные команды, позволяющие в интерактивном режиме задать внешние воздействия, прикладывая их непосредственно к элементам твердотельной модели. Препроцессор автоматически переносит граничные условия на КЭ-модель для построения тетраэдальной КЭ-модели изделия.

3. Осуществление расчетов в процессоре: генерация расчетных систем уравнений и их решение. Результатами работы КЭ-процессора являются значения искомых целевых функций.

4. Анализ результатов работы в постпроцессоре: анимация, отображение деформированного состояния и т.д.

Графика в САПР

Из истории. Интерес к синтезу изображений объясняется высокой информативностью последних. Информация, содержащаяся в изображении, представлена в наиболее концентрированной форме, и эта информация, как правило, более доступна для анализа: для ее восприятия получателю достаточно иметь относительно небольшой объем специальных знаний.

С начала использования ЭВМ возникла проблема представления получаемых данных в виде изображения. На начальном этапе программными средствами формировались различные символьные изображения: диаграммы, графики, условные схемы и т.д.

---

Формирование машинной графики как самостоятельного направления относится к началу 60-х годов, когда Айвеном Сазерлендом был создан первый специализированный пакет программного обеспечения машинной графики. В 60-е годы были сформулированы принципы рисования отрезками, удаления невидимых линий, методы отображения сложных поверхностей, определены методы формирования теней, учета освещенности сюжета. Первые работы были направлены в основном на развитие векторной графики.

70-е годы: значительное число теоретических и прикладных работ направлено на развитие методов отображения пространственных форм и объектов. Это направление принято называть трехмерной машинной (компьютерной) графикой. Математическое моделирование трехмерных сюжетов требует учета трехмерности пространства предметов, расположения в нем источников освещения и наблюдателя.

Отсюда направления работ:

– аппроксимация и представление сложных поверхностей;

– отображение узоров из них;

– генерирование текстур, рельефа;

– моделирование условий освещения;

– улучшение качества синтезированных изображений;

– повышение уровня их реалистичности;

– сглаживание погрешностей, возникающих в результате аппроксимации геометрической формы реальных тел и пространственной дискретизации изображения.

В отличие от фотографических, телевизионных, оптико-электронных и других аналогичных систем для систем машинной графики источником входной информации являются не сами физические процессы или объекты, а математические модели.

Эти модели в общем случае представляют упорядоченную совокупность данных, числовых характеристик, параметров, математических и логических зависимостей, отображающих структуру, свойства, взаимосвязи и отношения между объектом и его окружением. Математические модели обычно являются обобщенными и предназначаются для описания определенного класса объектов. При вводе конкретных значений параметров система машинной графики на основе общей модели синтезирует изображение и визуализирует его.

Трехмерная компьютерная графика

Описание геометрических форм

Описание поверхностей.

Параметрическое описание поверхностей.

Параметры – независимые величины, предназначенные для выделения элемента либо подмножества из множества. В геометрических задачах параметрами могут быть величины, выделяющие единственную фигуру из множества подобных фигур (задание в качестве параметров длины стороны треугольника и величины двух прилегающих к ней углов приводит к выделению единственного треугольника).

---

При выделении параметров важно учитывать области их существования (числа, выражающие длины сторон треугольника, могут быть только положительными и отличными от нуля, сумма любых двух из этих чисел должна быть больше третьего числа).

Поверхности, заданные в форме X = X (u, t), Y = Y (u, t), Z = Z (u, t), где u, t – параметры, изменяющиеся в заданных пределах, относятся к классу параметрических. Для одной фиксированной пары значений u, t можно вычислить только положение одной точки поверхности. Для полного представления о всей поверхности необходимо с определенным шагом перебрать множество пар u, t из диапазона их изменений, вычисляя для каждой пары значение X, Y, Z в трехмерном пространстве.

Эллипсоид вида



параметрически представляется в форме

,

г
де  – долгота,  – широта.  = [0; 2];  = [-/2; /2]

Особенно важными в практическом применении являются бикубические поверхности, с помощью которых можно описать гладкую поверхность произвольной формы. функция, составленная из нескольких смежных бикубических участков, будет обладать непрерывностью и гладкостью в местах стыка благодаря координатному совпадению смежных угловых точек и совпадению первых производных. Участок такой поверхности X = X (s, t), Y = Y (s, t), Z = Z (s, t) может быть представлен параметрически, например, уравнение для X = X (s, t):

,

где s, t – параметры, изменяющиеся в некотором фиксированном диапазоне; а₁₁,…,а₄₄ – постоянные коэффициенты в пределах данной поверхности, которые могут быть объединены в матрицу С_х размера 4х4.

Аналогичные выражения существуют для Y (s, t), Z (s, t), соответственно матрицы коэффициентов будут С_у, С_z.

Основной задачей конструирования криволинейной поверхности из бикубических участков является задание коэффициентов бикубического многочлена С_х, С_у, С_z внутри каждого участка через координаты общих угловых точек.

Обычно бикубические участки – это гладкие изогнутые четырехугольники, представление о которых могут дать листы металла, бумаги и др. материалов, обладающих упругостью.

Недостатки этой формы задания: трудоемкость описания и большие вычислительные затраты ввиду необходимости применения численных, а не аналитических методов математических решений.

---