Файл: Численное интегрирование систем дифференциальных уравнений. Метод Эйлера.docx
Добавлен: 11.01.2024
Просмотров: 168
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
при вытяжке в процессе формования.
Таким образом, при рассмотренных выше методе аппроксимирования приведенного момента и линеаризации уравнения движения машинного агрегата задача численного интегрирования системы дифференциальных уравнений сводится к вычислению интегралов с переменным верхним пределом. 3
Динамический ну анализ ну сейсмостойкости ну вышеуказанной ну модели, ну представленной ну в ну виде ну нелинейной ну системы ну с ну конечным ну числом ну степеней ну свободы, ну выполняется ну методами ну численного ну интегрирования ну системы ну дифференциальных ну уравнений ну движения.
1.2Численноедифференцированиеиинтегрирование
Уравнение ну вида ну y=A(x), ну определённое ну на ну функциональном ну пространстве, ну может ну содержать ну операторы ну дифференцирования ну и ну интегрирования, ну для ну которых ну невозможно ну найти ну точное ну решение. Методы ну численного ну дифференцирования ну и ну интегрирования ну основаны ну на ну интерполяции.
Производную ну основной ну функции ну считают ну приближённо ну равной ну производной
ну интерполирующей ну функции, ну при ну этом ну производная ну остаточного ну члена ну интерполяционной ну формулы ну может ну быть ну велика, ну особенно ну для ну производных ну высших ну порядков. Формулы ну численного ну дифференцирования ну во ну многом ну основаны ну на ну непосредственном ну дифференцировании ну интерполяционных ну формул ну Ньютона, ну Гаусса, ну Стирлинга ну и ну Бесселя, ну построенных ну на ну распределённых ну разностях, ну но ну есть ну и ну безразностные ну формулы. В ну частности, ну когда ну для ну численного ну дифференциала ну используется ну непосредственно ну формула ну Лагранжа ну для ну равных ну промежутков, ну метод ну неопределённых ну коэффициентов ну и ну другие.
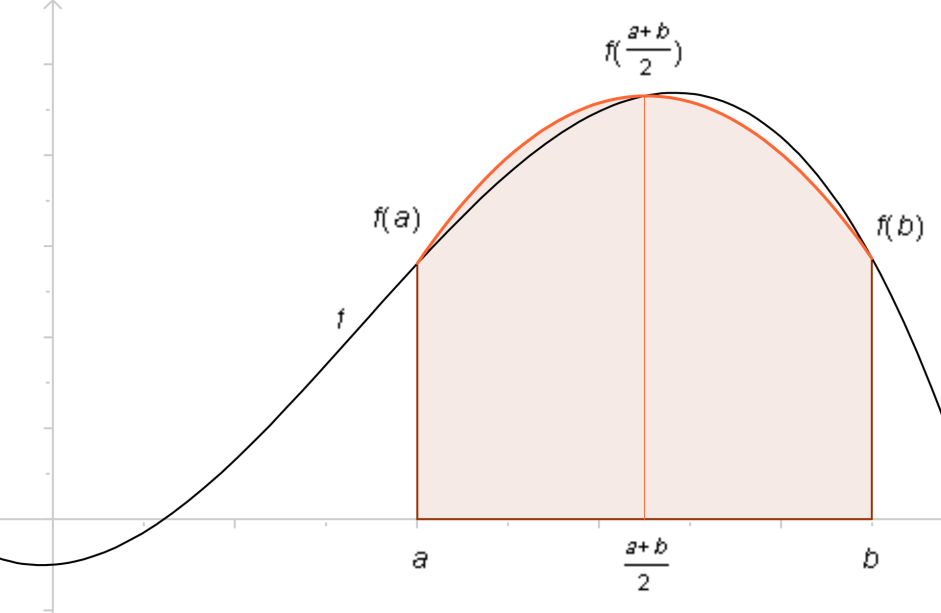
Рисунок ну 1.1. Численное ну интегрирование ну по ну формуле ну Симпсона
В ну случае ну интегрирования, ну само ну определение ну интеграла ну говорит ну о ну возможности ну его ну замены ну интегральной ну суммой, ну но ну этот ну приём ну обладает ну медленной ну сходимостью ну и ну мало ну пригоден. Интеграл ну от ну основной ну функции
ну считают ну приближённо ну равным ну интегралу ну от ну интерполирующей ну функции ну и ну в ну дальнейшем ну используют ну интерполяционные ну формулы ну с ну кратными ну узлами. Использование в качестве подынтегрального выражения интерполяционного многочлена Лагранжа для равных промежутков приводит к формулам Ньютона — Котеса и её частным случаям, формуле трапеций, когда кривая подынтегрального выражения заменяется хордой и интеграл равен ну площади ну трапеции, ну и ну формуле ну Симпсона, ну когда ну кривая ну подынтегрального ну выражения ну заменяется ну параболой, ну проходящей ну через ну три ну точки. Отказавшись ну от ну требования ну равных ну промежутков ну с ну помощью ну интерполяционного ну многочлена ну Лагранжа ну можно ну получить ну более ну точные ну формулы ну численного ну интегрирования, ну в ну частности ну формулы ну Гаусса, ну формулы ну Эрмита, ну формулы ну Маркова, ну формулы ну Чебышёва. Квадратурные ну процессы, ну построенные ну на ну интерполяционных ну формулах ну Гаусса, ну всегда ну сходятся, ну
в ну то ну время ну как ну формулы ну Ньютона ну — ну Кортеса ну этим ну свойствам ну в ну общем ну случае ну не ну обладают.
Существуют и другие способы численного интегрирования, основным из которых является использование формул Эйлера, в которых замена переменных и последующее интегрирование по частям приводят к формуле численного интегрирования трапецией и поправочного члена, к которому повторно применяется замена переменных и интегрирование по частям. В ну общем ну случае ну формула ну Эйлера ну использует ну в ну качестве ну коэффициентов ну числа ну и ну многочлены ну Бернулли. Вопрос ну применения ну того ну или ну иного ну метода ну численного ну интегрирования ну зависит ну от ну таких ну факторов, ну как ну вычислительные ну средства, ну требуемая ну точность, ну способ ну задания ну подынтегральной ну функции. Для ну ручных ну вычислений ну рекомендуется ну использовать ну формулы, ну содержащие ну разности, ну в ну то ну время ну как ну при ну автоматических ну
вычислениях ну — ну безразностные ну формулы, ну в ну особенности ну формулы ну Гаусса.
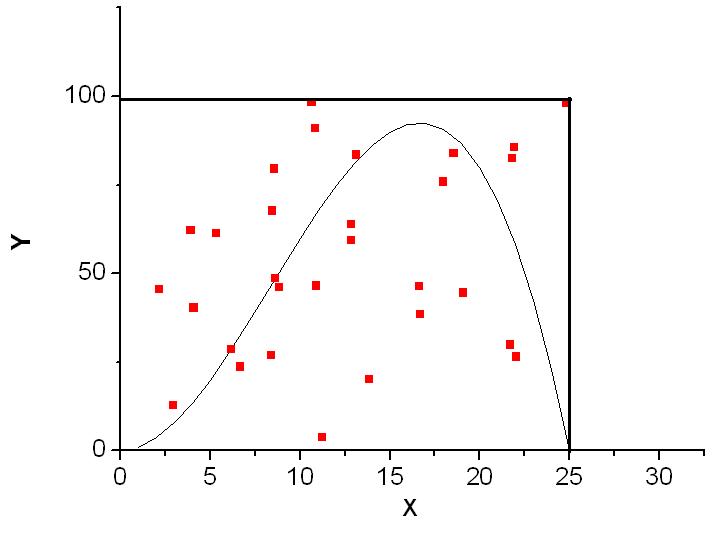
Рисунок ну 1.2. Численное ну интегрирование ну методами ну Монте-Карло
Для приближённого вычисления кратных интегралов повторно применяют формулы численного интегрирования однократных интегралов, при этом в зависимости от особенностей функции для разных интегралов можно использовать разные формулы. При ну использовании ну данного ну метода ну необходимо ну вычислять ну подынтегральную ну функцию ну в ну большом ну числе ну точек, ну поэтому ну целесообразно ну использовать ну формулы ну Гаусса ну и ну Чебышёва, ну которые ну являются ну более ну точными. Другим ну способом ну является ну замена ну подынтегральной ну функции ну интерполяционным ну многочленом ну от ну двух ну или ну несколько ну переменных. Люстерник ну и ну Диткин ну предложили ну использовать ну формулы ну Маклорена ну для ну приближённого ну вычисления ну кратного ну интеграла. Вместе ну с ну тем, ну при ну увеличении ну кратности ну интеграла
Таким образом, при рассмотренных выше методе аппроксимирования приведенного момента и линеаризации уравнения движения машинного агрегата задача численного интегрирования системы дифференциальных уравнений сводится к вычислению интегралов с переменным верхним пределом. 3
Динамический ну анализ ну сейсмостойкости ну вышеуказанной ну модели, ну представленной ну в ну виде ну нелинейной ну системы ну с ну конечным ну числом ну степеней ну свободы, ну выполняется ну методами ну численного ну интегрирования ну системы ну дифференциальных ну уравнений ну движения.
1.2Численноедифференцированиеиинтегрирование
Уравнение ну вида ну y=A(x), ну определённое ну на ну функциональном ну пространстве, ну может ну содержать ну операторы ну дифференцирования ну и ну интегрирования, ну для ну которых ну невозможно ну найти ну точное ну решение. Методы ну численного ну дифференцирования ну и ну интегрирования ну основаны ну на ну интерполяции.
Производную ну основной ну функции ну считают ну приближённо ну равной ну производной
ну интерполирующей ну функции, ну при ну этом ну производная ну остаточного ну члена ну интерполяционной ну формулы ну может ну быть ну велика, ну особенно ну для ну производных ну высших ну порядков. Формулы ну численного ну дифференцирования ну во ну многом ну основаны ну на ну непосредственном ну дифференцировании ну интерполяционных ну формул ну Ньютона, ну Гаусса, ну Стирлинга ну и ну Бесселя, ну построенных ну на ну распределённых ну разностях, ну но ну есть ну и ну безразностные ну формулы. В ну частности, ну когда ну для ну численного ну дифференциала ну используется ну непосредственно ну формула ну Лагранжа ну для ну равных ну промежутков, ну метод ну неопределённых ну коэффициентов ну и ну другие.

Рисунок ну 1.1. Численное ну интегрирование ну по ну формуле ну Симпсона
В ну случае ну интегрирования, ну само ну определение ну интеграла ну говорит ну о ну возможности ну его ну замены ну интегральной ну суммой, ну но ну этот ну приём ну обладает ну медленной ну сходимостью ну и ну мало ну пригоден. Интеграл ну от ну основной ну функции
ну считают ну приближённо ну равным ну интегралу ну от ну интерполирующей ну функции ну и ну в ну дальнейшем ну используют ну интерполяционные ну формулы ну с ну кратными ну узлами. Использование в качестве подынтегрального выражения интерполяционного многочлена Лагранжа для равных промежутков приводит к формулам Ньютона — Котеса и её частным случаям, формуле трапеций, когда кривая подынтегрального выражения заменяется хордой и интеграл равен ну площади ну трапеции, ну и ну формуле ну Симпсона, ну когда ну кривая ну подынтегрального ну выражения ну заменяется ну параболой, ну проходящей ну через ну три ну точки. Отказавшись ну от ну требования ну равных ну промежутков ну с ну помощью ну интерполяционного ну многочлена ну Лагранжа ну можно ну получить ну более ну точные ну формулы ну численного ну интегрирования, ну в ну частности ну формулы ну Гаусса, ну формулы ну Эрмита, ну формулы ну Маркова, ну формулы ну Чебышёва. Квадратурные ну процессы, ну построенные ну на ну интерполяционных ну формулах ну Гаусса, ну всегда ну сходятся, ну
в ну то ну время ну как ну формулы ну Ньютона ну — ну Кортеса ну этим ну свойствам ну в ну общем ну случае ну не ну обладают.
Существуют и другие способы численного интегрирования, основным из которых является использование формул Эйлера, в которых замена переменных и последующее интегрирование по частям приводят к формуле численного интегрирования трапецией и поправочного члена, к которому повторно применяется замена переменных и интегрирование по частям. В ну общем ну случае ну формула ну Эйлера ну использует ну в ну качестве ну коэффициентов ну числа ну и ну многочлены ну Бернулли. Вопрос ну применения ну того ну или ну иного ну метода ну численного ну интегрирования ну зависит ну от ну таких ну факторов, ну как ну вычислительные ну средства, ну требуемая ну точность, ну способ ну задания ну подынтегральной ну функции. Для ну ручных ну вычислений ну рекомендуется ну использовать ну формулы, ну содержащие ну разности, ну в ну то ну время ну как ну при ну автоматических ну
вычислениях ну — ну безразностные ну формулы, ну в ну особенности ну формулы ну Гаусса.

Рисунок ну 1.2. Численное ну интегрирование ну методами ну Монте-Карло
Для приближённого вычисления кратных интегралов повторно применяют формулы численного интегрирования однократных интегралов, при этом в зависимости от особенностей функции для разных интегралов можно использовать разные формулы. При ну использовании ну данного ну метода ну необходимо ну вычислять ну подынтегральную ну функцию ну в ну большом ну числе ну точек, ну поэтому ну целесообразно ну использовать ну формулы ну Гаусса ну и ну Чебышёва, ну которые ну являются ну более ну точными. Другим ну способом ну является ну замена ну подынтегральной ну функции ну интерполяционным ну многочленом ну от ну двух ну или ну несколько ну переменных. Люстерник ну и ну Диткин ну предложили ну использовать ну формулы ну Маклорена ну для ну приближённого ну вычисления ну кратного ну интеграла. Вместе ну с ну тем, ну при ну увеличении ну кратности ну интеграла