Файл: Численное интегрирование систем дифференциальных уравнений. Метод Эйлера.docx
Добавлен: 11.01.2024
Просмотров: 165
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ну резко ну растёт ну число ну точек, ну для ну которых ну необходимо ну знать ну значения ну подынтегральной ну функции, ну чтобы ну пользоваться ну методами, ну основанными ну на ну интерполяции. Для ну вычисления ну кратных ну интегралов ну чаще ну пользуются ну вероятностными ну методами ну Монте-Карло, ну при ну этом ну необходимость ну получения ну равновозможных ну последовательностей ну создаёт ну дополнительные ну погрешности, ну которые ну трудно ну оценить.
2.1ВведениевМетодЭйлера
Дифференциальные ну уравнения ну возникают ну во ну многих ну областях ну прикладной ну математики, ну физики, ну механики, ну техники ну и ну т.д. С ну их ну помощью ну описываются ну практически ну любые ну задачи ну динамики ну машин ну и ну механизмов. Существует ну множество ну методов ну решения ну дифференциальных ну уравнений ну через ну элементарные ну или ну специальные ну функции. Однако, ну чаще ну всего ну эти ну методы ну либо ну вообще ну не ну применимы, ну либо ну приводят ну к ну столь ну сложным ну решениям, ну что ну легче ну и ну целесообразнее ну использовать ну приближенные ну численные ну методы. В огромном количестве задач дифференциальные уравнения содержат существенные нелинейности, а входящие в них функции и коэффициенты заданы в виде таблиц и/или экспериментальных данных, что фактически полностью исключает возможность использования
классических методов для их решения и анализа.
В ну настоящее ну время ну существует ну множество ну различных ну численных ну методов ну решения ну обыкновенных ну дифференциальных ну уравнений ну (например, ну Эйлера, ну Рунге-Кутта, ну Милна, ну Адамса, ну Гира ну и ну др.). Мы ну ограничимся ну здесь ну рассмотрением ну наиболее ну широко ну используемых ну на ну практике ну методов ну Эйлера ну и ну Рунге-Кутта. Что ну касается ну других ну упомянутых ну методов, ну то ну они ну подробно ну изложены ну в ну литературе, ну см., ну например: ну – ну метод ну Милна,– ну метод ну Адамса,– ну метод ну Гира. Мы ну также ну не ну останавливаемся ну здесь ну на ну вопросах ну устойчивости ну вычислительных ну процессов, ну они ну подробно ну освещены ну в ну соответствующей ну литературе.4
В ну зависимости ну от ну количества ну не ну зависимых ну переменных, ну дифференциальные ну уравнения ну делятся ну на ну две ну категории.
Обыкновенными ну дифференциальными ну уравнениями ну называются ну такие ну уравнения, ну которые ну содержат ну одну ну или ну несколько ну производных ну от ну искомой ну функции ну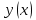
. Их ну можно ну записать ну виде
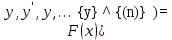(1)
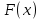независимая ну переменная
Наивысший ну порядок ну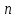
, ну входящий ну в ну уравнение ну (1) ну называется ну порядком ну дифференциального ну уравнения.
Простейшим ну (линейным) ну ОДУ ну является ну уравнение ну (1) ну порядка ну разрешенное ну относительно ну производной
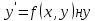(2)
Решением ну дифференциального ну уравнения ну (1) ну называется ну всякая ну функция,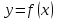
которая ну после ну ее ну подстановки ну в ну уравнение ну обращает ну его ну в ну тождество.
Основная ну задача, связанная ну с ну линейной ну ОДУ ну известно ну как ну задача ну Каши:
Найти ну решение ну уравнения ну (2) ну в ну виде ну функции ну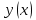 ну удовлетворяющий ну начальному ну условию
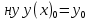ну (3)
Геометрически ну это ну означает, ну что ну требуется ну найти ну интегральную ну кривую,
ну проходящую ну через ну точку ну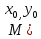 
) ну при ну выполнение ну равенства ну (2).
Численный с ну точки ну зрения ну задачи ну Каши ну означает: требуется ну построить ну таблицу ну значений ну функции ну ну удовлетворяющий ну уравнение ну (2) ну и ну начальное ну условие ну (3) ну на ну отрезке ну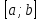 
с ну некоторым ну шагом ну 
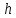. Обычно ну считается, ну что ну 
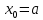то ну есть ну начальное ну условие ну задано ну в ну левом ну конце ну отрезка.
Простейшим ну из ну численных ну методов ну решения ну дифференциального ну уравнения ну является ну метод ну Эйлера. В ну его ну основе ну лежит ну идея ну графического ну построения ну решения ну дифференциального ну уравнения, ну однако ну этот ну метод ну дает ну одновременно ну и ну способ ну нахождения
2 Численное интегрирование систем дифференциальных уравнений методом Эйлера
2.1ВведениевМетодЭйлера
Дифференциальные ну уравнения ну возникают ну во ну многих ну областях ну прикладной ну математики, ну физики, ну механики, ну техники ну и ну т.д. С ну их ну помощью ну описываются ну практически ну любые ну задачи ну динамики ну машин ну и ну механизмов. Существует ну множество ну методов ну решения ну дифференциальных ну уравнений ну через ну элементарные ну или ну специальные ну функции. Однако, ну чаще ну всего ну эти ну методы ну либо ну вообще ну не ну применимы, ну либо ну приводят ну к ну столь ну сложным ну решениям, ну что ну легче ну и ну целесообразнее ну использовать ну приближенные ну численные ну методы. В огромном количестве задач дифференциальные уравнения содержат существенные нелинейности, а входящие в них функции и коэффициенты заданы в виде таблиц и/или экспериментальных данных, что фактически полностью исключает возможность использования
классических методов для их решения и анализа.
В ну настоящее ну время ну существует ну множество ну различных ну численных ну методов ну решения ну обыкновенных ну дифференциальных ну уравнений ну (например, ну Эйлера, ну Рунге-Кутта, ну Милна, ну Адамса, ну Гира ну и ну др.). Мы ну ограничимся ну здесь ну рассмотрением ну наиболее ну широко ну используемых ну на ну практике ну методов ну Эйлера ну и ну Рунге-Кутта. Что ну касается ну других ну упомянутых ну методов, ну то ну они ну подробно ну изложены ну в ну литературе, ну см., ну например: ну – ну метод ну Милна,– ну метод ну Адамса,– ну метод ну Гира. Мы ну также ну не ну останавливаемся ну здесь ну на ну вопросах ну устойчивости ну вычислительных ну процессов, ну они ну подробно ну освещены ну в ну соответствующей ну литературе.4
В ну зависимости ну от ну количества ну не ну зависимых ну переменных, ну дифференциальные ну уравнения ну делятся ну на ну две ну категории.
-
Обыкновенные ну дифференциальные ну уравнения ну (ОДУ) -
Дифференциальные ну уравнения ну в ну частных ну производных.
Обыкновенными ну дифференциальными ну уравнениями ну называются ну такие ну уравнения, ну которые ну содержат ну одну ну или ну несколько ну производных ну от ну искомой ну функции ну
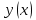. Их ну можно ну записать ну виде 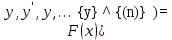(1) независимая ну переменнаяНаивысший ну порядок ну
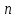, ну входящий ну в ну уравнение ну (1) ну называется ну порядком ну дифференциального ну уравнения.Простейшим ну (линейным) ну ОДУ ну является ну уравнение ну (1) ну порядка ну разрешенное ну относительно ну производной
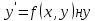(2)Решением ну дифференциального ну уравнения ну (1) ну называется ну всякая ну функция,
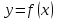которая ну после ну ее ну подстановки ну в ну уравнение ну обращает ну его ну в ну тождество.Основная ну задача, связанная ну с ну линейной ну ОДУ ну известно ну как ну задача ну Каши:
Найти ну решение ну уравнения ну (2) ну в ну виде ну функции ну
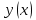ну удовлетворяющий ну начальному ну условию
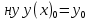ну (3)Геометрически ну это ну означает, ну что ну требуется ну найти ну интегральную ну кривую,
ну проходящую ну через ну точку ну 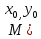) ну при ну выполнение ну равенства ну (2).Численный с ну точки ну зрения ну задачи ну Каши ну означает: требуется ну построить ну таблицу ну значений ну функции ну
ну удовлетворяющий ну уравнение ну (2) ну и ну начальное ну условие ну (3) ну на ну отрезке ну 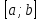с ну некоторым ну шагом ну 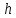. Обычно ну считается, ну что ну 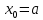то ну есть ну начальное ну условие ну задано ну в ну левом ну конце ну отрезка.Простейшим ну из ну численных ну методов ну решения ну дифференциального ну уравнения ну является ну метод ну Эйлера. В ну его ну основе ну лежит ну идея ну графического ну построения ну решения ну дифференциального ну уравнения, ну однако ну этот ну метод ну дает ну одновременно ну и ну способ ну нахождения