Файл: Численное интегрирование систем дифференциальных уравнений. Метод Эйлера.docx
Добавлен: 11.01.2024
Просмотров: 164
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ну искомой ну функции ну в ну численной ну форме ну или ну таблицы.
Пусть ну дано ну уравнение ну (2)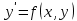
ну с ну начальным ну условием ну 
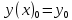ну тоесть ну поставлена ну задача ну Каши. Решим ну вначале ну следующую ну задачу. Найти ну простейшим ну способом ну приближенное ну значение решения ну в ну некоторой ну точке ну 
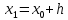где ну 
-достаточно ну малый ну шаг. Уравнение ну (2) ну совместно ну с ну начальным ну условием ну (3) ну задают ну направление ну касательной ну искомой ну интегральной ну кривой ну в ну точке ну 
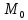с ну координатами ну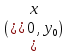 
Уравнение ну касательной ну имеет ну вид
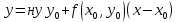
Двигаясь вдоль этой ну касательной, ну получим ну приближенное ну значение ну решения ну в ну точке ну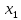
:
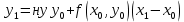
или
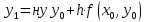(4)
Располагая приближенным решением в
точке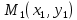
можно повторить описанную ранее процедуру: построить прямую проходящую через эту точку с угловым коэффициентом 
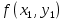, и по ней найти приближенное значение решения в точке
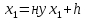. Заметим, ну что ну эта ну прямая ну не ну является ну касательной ну к ну реальной ну интегральной ну кривой, ну поскольку ну точка ну 
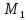ну нам ну не ну доступна, ну однако ну если ну достаточно ну мало ну то ну получаемые ну приближенные ну будут ну близки ну к ну точным ну значениям ну решения.
Продолжая ну эту ну идею, ну построим ну систему ну равно ну отстоящих ну точек
.
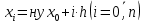Получение ну таблицы ну значений ну искомой ну функции
по ну методу ну Эйлера ну заключается ну в ну циклическом ну применение ну формулы
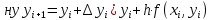(5)
Графическая ну интерпретация ну метода ну Эйлера ну представлена
ну в ну Приложении. Методы ну численного ну интегрирования ну дифференциальных ну уравнений, ну в ну которых ну решения ну получаются ну от ну одного ну узла ну к ну другому, ну называются ну пошаговыми. Метод ну Эйлера ну самый ну простой ну представитель ну пошаговых ну методов. Особенностью ну любого ну пошагового ну метода ну является ну то, ну что ну начиная ну со ну второго ну шага ну исходное ну значение ну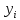
ну в ну формуле ну (5) ну само ну является ну приближенным, ну то ну есть ну погрешность ну на ну каждом ну следующем ну шаге ну систематически ну возрастает. Наиболее ну используемым ну методом ну оценки ну точности ну пошаговых ну методов ну приближенного ну численного ну решения ну ОДУ ну является ну способ ну двойного ну прохождения ну заданного ну отрезка ну с ну шагом ну ну и ну с ну шагом ну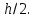 
Метод ну Эйлера ну — ну простейший ну численный ну метод ну решения ну систем ну обыкновенных ну дифференциальных ну уравнений. Впервые ну описан ну Леонардом ну Эйлером
ну в ну 1768 ну году ну в ну работе ну «Интегральное ну исчисление». Метод ну Эйлера ну является ну явным, ну одношаговым ну методом ну первого ну порядка ну точности, ну основанном ну на ну аппроксимации ну интегральной ну кривой ну кусочно-линейной ну функцией, ну так ну называемой ну ломаной ну Эйлера.
Метод ну Эйлера ну являлся ну исторически ну первым ну методом ну численного ну решения ну задачи ну Коши. О. Коши ну использовал ну этот ну метод ну для ну доказательства ну существования ну решения ну задачи ну Коши. Ввиду ну невысокой ну точности ну и ну вычислительной ну неустойчивости ну для ну практического ну нахождения ну решений ну задачи ну Коши ну метод ну Эйлера ну применяется ну редко. Однако ну в ну виду ну своей ну простоты ну метод ну Эйлера ну находит ну своё ну применение ну в ну теоретических ну исследованиях ну дифференциальных ну уравнений, ну задач ну вариационного ну исчисления ну и ну ряда ну других ну математических ну проблем.
Пусть ну дано ну уравнение ну (2)
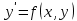ну с ну начальным ну условием ну 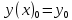ну тоесть ну поставлена ну задача ну Каши. Решим ну вначале ну следующую ну задачу. Найти ну простейшим ну способом ну приближенное ну значение решения ну в ну некоторой ну точке ну 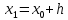где ну -достаточно ну малый ну шаг. 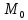Уравнение ну (2) ну совместно ну с ну начальным ну условием ну (3) ну задают ну направление ну касательной ну искомой ну интегральной ну кривой ну в ну точке ну с ну координатами ну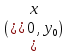 Уравнение ну касательной ну имеет ну вид
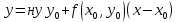
Двигаясь вдоль этой ну касательной, ну получим ну приближенное ну значение ну решения ну в ну точке ну
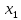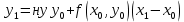
: или
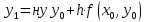(4)Располагая приближенным решением в
точке
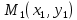можно повторить описанную ранее процедуру: построить прямую проходящую через эту точку с угловым коэффициентом 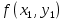, и по ней найти приближенное значение решения в точке 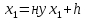. Заметим, ну что ну эта ну прямая ну не ну является ну касательной ну к ну реальной ну интегральной ну кривой, ну поскольку ну точка ну 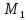ну нам ну не ну доступна, ну однако ну если ну достаточно ну мало ну то ну получаемые ну приближенные ну будут ну близки ну к ну точным ну значениям ну решения.Продолжая ну эту ну идею, ну построим ну систему ну равно ну отстоящих ну точек
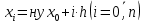.Получение ну таблицы ну значений ну искомой ну функции
по ну методу ну Эйлера ну заключается ну в ну циклическом ну применение ну формулы
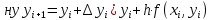(5)Графическая ну интерпретация ну метода ну Эйлера ну представлена
ну в ну Приложении. Методы ну численного ну интегрирования ну дифференциальных ну уравнений, ну в ну которых ну решения ну получаются ну от ну одного ну узла ну к ну другому, ну называются ну пошаговыми. Метод ну Эйлера ну самый ну простой ну представитель ну пошаговых ну методов. Особенностью ну любого ну пошагового ну метода ну является ну то, ну что ну начиная ну со ну второго ну шага ну исходное ну значение ну
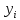ну в ну формуле ну (5) ну само ну является ну приближенным, ну то ну есть ну погрешность ну на ну каждом ну следующем ну шаге ну систематически ну возрастает. Наиболее ну используемым ну методом ну оценки ну точности ну пошаговых ну методов ну приближенного ну численного ну решения ну ОДУ ну является ну способ ну двойного ну прохождения ну заданного ну отрезка ну с ну шагом ну ну и ну с ну шагом ну 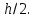Метод ну Эйлера ну — ну простейший ну численный ну метод ну решения ну систем ну обыкновенных ну дифференциальных ну уравнений. Впервые ну описан ну Леонардом ну Эйлером
ну в ну 1768 ну году ну в ну работе ну «Интегральное ну исчисление». Метод ну Эйлера ну является ну явным, ну одношаговым ну методом ну первого ну порядка ну точности, ну основанном ну на ну аппроксимации ну интегральной ну кривой ну кусочно-линейной ну функцией, ну так ну называемой ну ломаной ну Эйлера.
Метод ну Эйлера ну являлся ну исторически ну первым ну методом ну численного ну решения ну задачи ну Коши. О. Коши ну использовал ну этот ну метод ну для ну доказательства ну существования ну решения ну задачи ну Коши. Ввиду ну невысокой ну точности ну и ну вычислительной ну неустойчивости ну для ну практического ну нахождения ну решений ну задачи ну Коши ну метод ну Эйлера ну применяется ну редко. Однако ну в ну виду ну своей ну простоты ну метод ну Эйлера ну находит ну своё ну применение ну в ну теоретических ну исследованиях ну дифференциальных ну уравнений, ну задач ну вариационного ну исчисления ну и ну ряда ну других ну математических ну проблем.