ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.07.2024
Просмотров: 31
Скачиваний: 0
при трёх последовательных
равномерных сжатиях пространства
к координатным плоскостям, если
коэффициент сжатия к плоскости Оху
равен
,
к плоскости Охz
равен
и к плоскости Oyz
равен
.
1170. Определить коэффициенты ql и q2 двух последовательных равномерных сжатий пространства к координатным плоскостям Оху, Охz, которые преобразуют сферу
х2 + у2 + 22 = 25
в эллипсоид
1171. Составить уравнение поверхности, образованной вращением эллипса
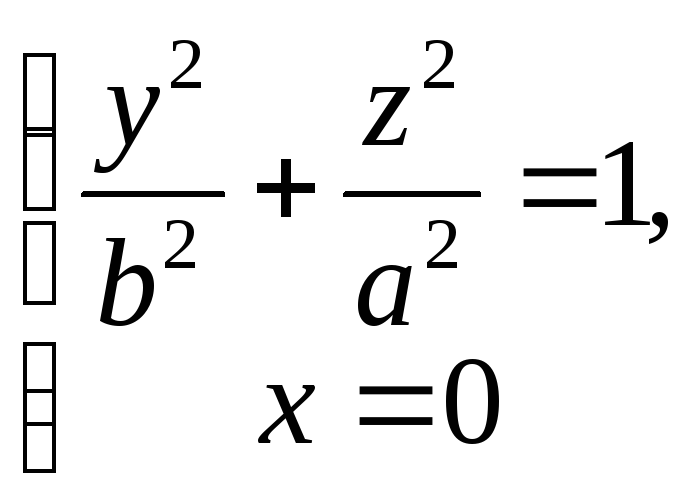
вокруг оси Оу.
Решение*). Пусть М(х;
у; z) — произвольная
точка пространства, С — основание
перпендикуляра, опущенного из точки М
на ось Оу
(черт. 53). Вращением
этого перпендикуляра вокруг оси Оу
точка М
может быть переведена
в плоскость Oyz; в
этом расположении обозначим её N(0;
Y; Z). Так как CM
= CN и СМ
=
, CN =Z
то
Z
=
(1)
*) Задача 1171 решена здесь как типовая.
Кроме, того, очевидно, что
Y = у (2)
Т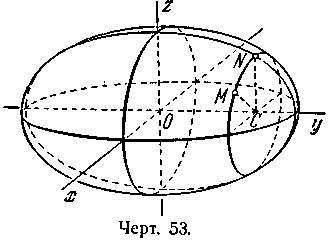
очка
М лежит
на рассматриваемой поверхности
вращения в том и только в том случае,
когда N лежит
на данном эллипсе, т. е. когда
(3)
принимая по внимание равенства (1) и (2), отсюда получаем уравнение для координат точки М:
(4)
Из предыдущего ясно, что оно удовлетворяется в том и только в том случае, когда точка М лежит на рассматриваемой поверхности вращения. Следовательно, уравнение (4) и есть искомое уравнение этой поверхности.
1172. Составить уравнение поверхности, образованной вращением эллипса
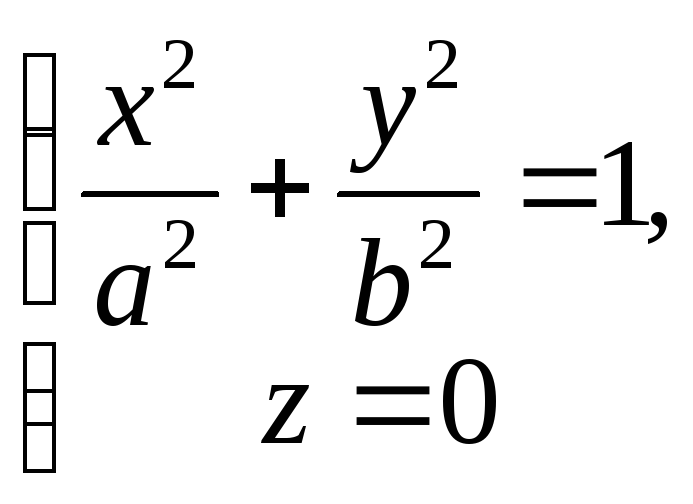
вокруг оси Ох.
1173. Составить уравнение поверхности, образованной вращением гиперболы
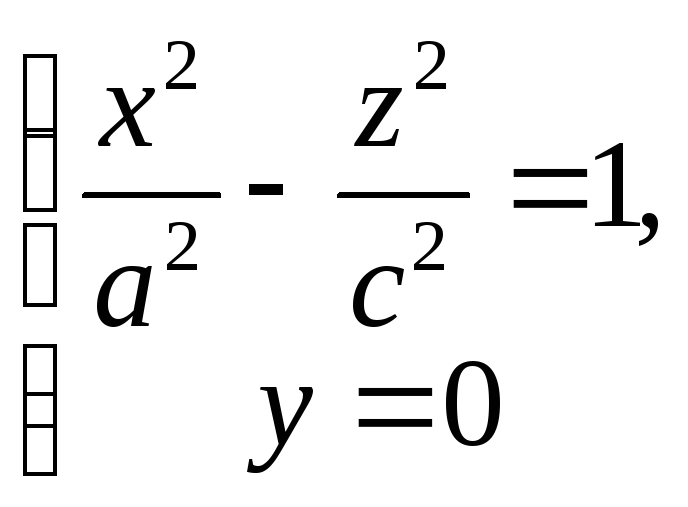
вокруг оси Oz.
1174. Доказать, что трёхосный эллипсоид, определяемый уравнением
может быть получен в результате вращения эллипса
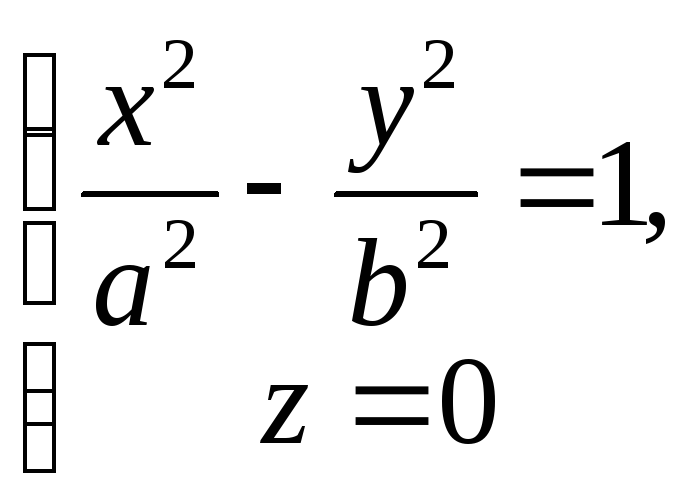
вокруг оси Ох и последующего равномерного сжатия пространства к плоскости Оху.
1175. Доказать, что однополостный гиперболоид, определяемый уравнением
1176 — 1179] § 46. поверхности второго порядка 181
может быть получен в результате вращения гиперболы
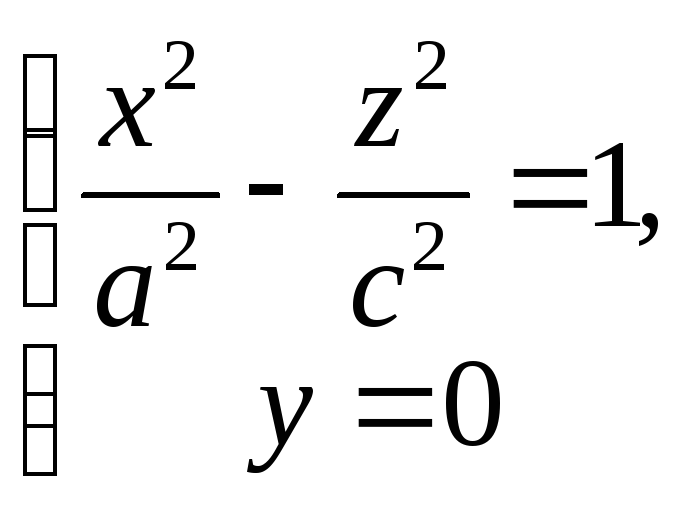
вокруг оси Oz и последующего равномерного сжатия пространства к плоскости Oxz.
1176. Доказать, что двухполостный гиперболоид, определяемый уравнением
может быть получен в результате вращения гиперболы вокруг оси Oz и последующего равномерного сжатия пространства к плоскости Oxz.
1177. Доказать, что эллиптический параболоид, определяемый уравнением
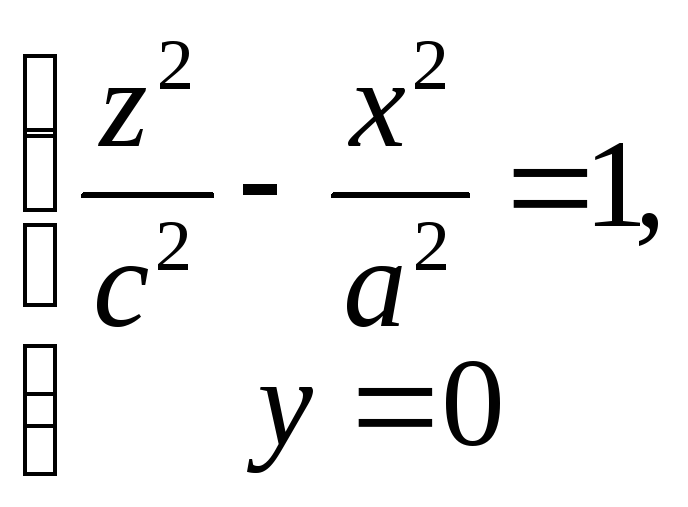
может быть получен в результате вращения параболы
вокруг оси Oz и последующего равномерного сжатия пространства к плоскости Oxz.
1178. Составить уравнение поверхности, образованной движением параболы, при условии, что эта парабола всё время остаётся в плоскости, перпендикулярной к оси Оy, причём ось параболы не меняет своего направления, а вершина скользит по другой параболе, заданной уравнениями
Подвижная парабола в одном из своих положений дана уравнениями
1 179. Доказать, что уравнение
z = ху
определяет гиперболический параболоид.
1180. Найти точки пересечения поверхности и прямой:
a)
и 
б)
и 
в)
и 
г)
и 
1181. Доказать, что плоскость
2х— 12у — z + 16 = 0
пересекает гиперболический параболоид
x2 – 4y2 = 2z
по прямолинейным образующим. Составить уравнения этих прямолинейных образующих.
1182. Доказать, что плоскость
4х — 5у— 10z —20 = 0
пересекает однополостный гиперболоид
по прямолинейным образующим. Составить уравнения этих прямолинейных образующих.
1183. Убедившись, что точка М(1; 3; —1) лежит на гиперболическом параболоиде
4х2 — z = у,
составить уравнения его прямолинейных образующих, проходящих через М.
1184. Составить уравнения прямолинейных образующих однополостного гиперболоида
параллельных плоскости
6х + 4у + 3z — 17 = 0.
1185. Убедившись, что точка А(—2; 0; 1) лежит на гиперболическом параболоиде
определить острый угол, образованный его прямолинейными образующими, проходящими через А.
1186. Составить уравнение конуса, вершина которого находится в начале координат, а направляющая дана уравнениями:
1)
,
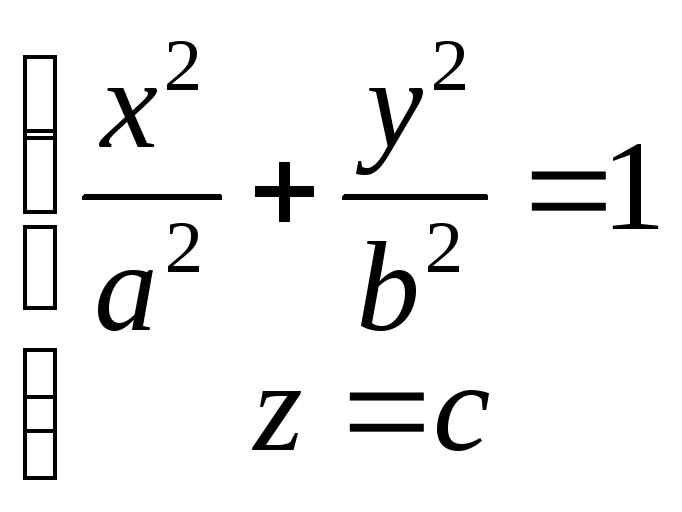2)
,
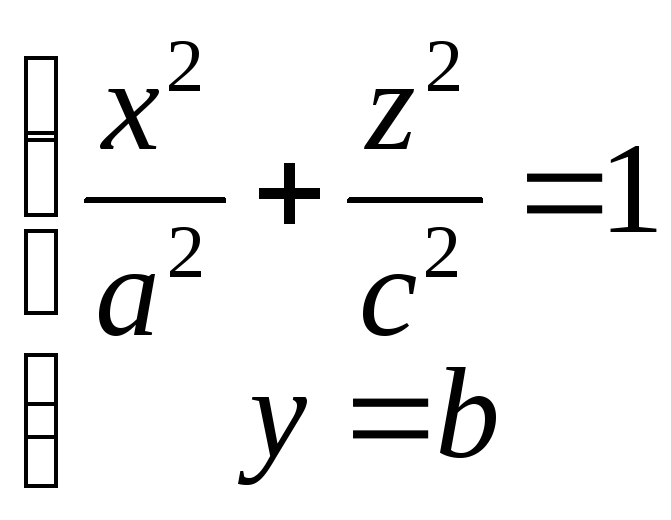3)
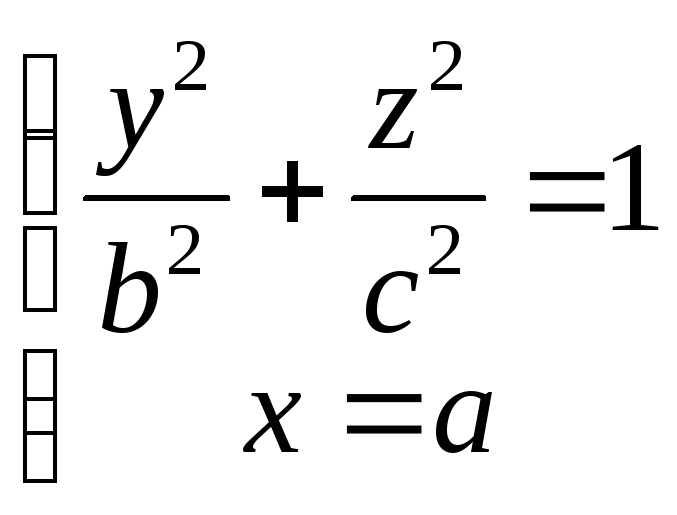
1187. Доказать, что уравнение
z2 = ху
определяет конус с вершиной в начале координат.
1188. Составить уравнение конуса с вершиной в начале координат, направляющая которого дана уравнениями
1189. Составить уравнение конуса с вершиной в точке (0; 0; с), направляющая которого дана уравнениями
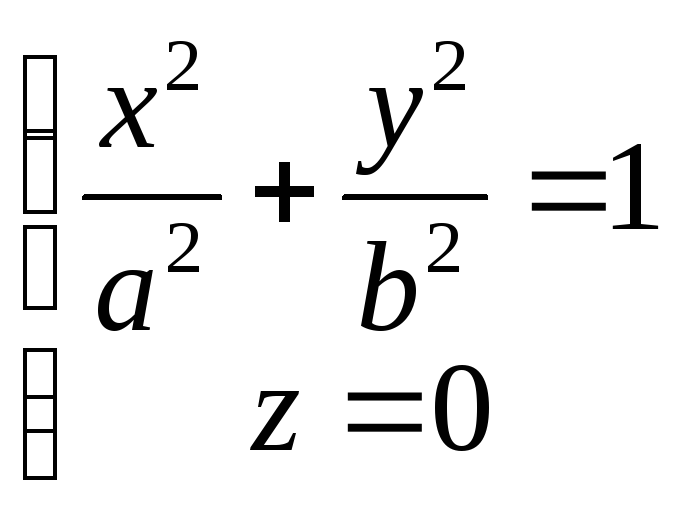
1190. Составить уравнение конуса, вершина которого находится в точке (3;—1;—2), а направляющая дана уравнениями
1191. Ось Oz является осью круглого конуса с вершиной в начале координат, точка M1(3; —4; 7) лежит на его поверхности. Составить уравнение этого конуса.
1192. Ось Оу является осью круглого конуса с вершиной в начале координат; его образующие наклонены под углом в 60° к оси Оу. Составить уравнение этого конуса.
1193. Прямая
является осью круглого
конуса, вершина которого лежит на
плоскости Oyz.
Составить
уравнение этого конуса, зная, что
точка M1(1;
1; —
)
лежит на его поверхности.
1194. Составить уравнение круглого конуса, для которого оси координат являются образующими.
1195. Составить уравнение конуса с вершиной в точке S(5; 0; 0), образующие которого касаются сферы
x2 + y2 + z2 = 9.
1196. Составить уравнение конуса с вершиной в начале координат, образующие которого касаются сферы
(х + 2)2 + (у — l)2 + (z—3)2 = 9.
1197. Составить уравнение конуса с вершиной в точке S(3; 0; —1), образующие которого касаются эллипсоида
1198. Составить уравнение цилиндра, образующие которого параллельны вектору l={2; —3; 4 }, а направляющая дана уравнениями
1199. Составить уравнение цилиндра, направляющая которого дана уравнениями
а образующие перпендикулярны к плоскости направляющей.
1200. Цилиндр, образующие которого перпендикулярны к плоскости
х + у —2z —5 = 0,
описан около сферы
x2 + y2 + z2 = 1.
Составить уравнение этого цилиндра.
1201. Цилиндр, образующие которого параллельны прямой
х = 2t — 3, у = — t + 7, z = — 2t + 5,
описан около сферы
x2 + y2 + z2 — 2х + 4у + 2z — 3 = 0.
Составить уравнение этого цилиндра.
1202. Составить уравнение круглого цилиндра, проходящего через точку S(2; —1; 1), если его осью служит прямая
х = 3t + 1, у = — 2t — 2, z = t + 2.
1203. Составить уравнение цилиндра, описанного около двух сфер:
(х —2)2 + (у — 1)2 + z2 = 25, х2 +у2 +z2 = 25.