Файл: 1 Схема планировочной организации земельного участка 1 Характеристика земельного участка.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.10.2023
Просмотров: 268
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1 Схема планировочной организации земельного участка
1.1 Характеристика земельного участка
1.2 Технико-экономические показатели земельного участка
2 Архитектурно-строительные решения
2.1 Технологический процесс эксплуатации здания
3.1 Расчёт усилий в конструкциях каркаса здания
3.1.1 Назначение стали для конструкций и материалов для сварки
3.4 Конструктивный расчёт элементов каркаса
3.5.2 Проверка устойчивости колонны
1OZ1 1
Коэффициент расчетной длины в плоскости X1OY1 1
Расстояние между точками раскрепления из плоскости изгиба 2,669 м
Сечение
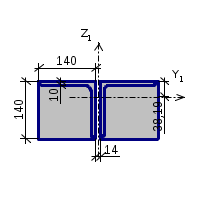
Профиль: Уголок равнополочный по ГОСТ 8509-93 L140x10
Коэффициент использования 0,41 - Предельная гибкость в плоскости XOZ
Конструктивная группа Раскосы. Элемент № 43
Сталь: C245
Длина элемента 2,28 м
Предельная гибкость для сжатых элементов: 180 - 60
Предельная гибкость для растянутых элементов: 400
Коэффициент условий работы 1
Коэффициент надежности по ответственности 1
Неупругая работа сечения не допускается
Коэффициент расчетной длины в плоскости X1OZ1 1
Коэффициент расчетной длины в плоскости X1OY1 1
Расстояние между точками раскрепления из плоскости изгиба 2,282 м
Сечение
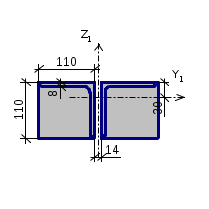 Профиль: Уголок равнополочный по ГОСТ 8509-93 L110x8
Профиль: Уголок равнополочный по ГОСТ 8509-93 L110x8
Коэффициент использования 0,77 - Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики
Конструктивная группа Стойки. Элемент № 35
Сталь: C245
Длина элемента 2,89 м
Предельная гибкость для сжатых элементов: 180 - 60
Предельная гибкость для растянутых элементов: 400
Коэффициент условий работы 1
Коэффициент надежности по ответственности 1
Неупругая работа сечения не допускается
Коэффициент расчетной длины в плоскости X1OZ1 1
Коэффициент расчетной длины в плоскости X1OY1 1
Расстояние между точками раскрепления из плоскости изгиба 2,889 м
Сечение
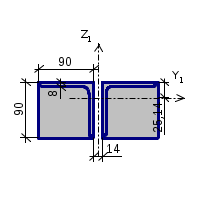
Профиль: Уголок равнополочный по ГОСТ 8509-93 L90x8
Коэффициент использования 0,7 - Предельная гибкость в плоскости XOZ
3.5 Расчет колонны
Колонна сплошного сечения выполнена из прокатного широкополочного двутавра, высотой 8 м. Имеет шарнирное сопряжение с фермой, и жесткое - с фундаментом. Материал колонны – сталь С235, бетон фундамента В20.
Так как колонна имеет сплошное сечение, то принимаем двутавр высотой hв=400 мм (рисунок 20).
Для симметричного двутавра:
i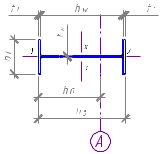 x≈0,42*hв, Рисунок 3.11 Сечение колонны
x≈0,42*hв, Рисунок 3.11 Сечение колонны
ρх≈0,35*hв.
ix≈0,42*400=294 мм;
ρх≈0,35*400=245 мм.
Условная гибкость:
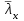 =(lx2/ix)*(Ry/E)0.5,
=(lx2/ix)*(Ry/E)0.5,
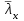 =(21600/294)*(240/206000)0.5=2.51.
=(21600/294)*(240/206000)0.5=2.51.
Относительный эксцентриситет:
mx=ex/ρx=M1/(N1*ρx),
mx=765.853*103/(646.32*245)=4.84.
Примем в первом приближении Аf/Аw=1, тогда коэффициент влияния формы сечения:
η=(1.90-0.1*mx)-0.02*(6-mx)*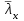 ,
,
η=(1.90-0.1*4.84)-0.02*(6-4.84)*2.51=1.36.
Приведенный относительный эксцентриситет:
mx ef=η*mx,
mx ef=1.36*4.84=6.57.
По таблице 74 СП II-23-81* находим φе=0.168.
Компоновка сечения.
Принимаем толщину полок tf=16,5 мм.
Высота стенки:
hw=hв-2*tf,
hw=700-2*18=664 мм.
Условие местной устойчивости стенки при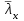 >0.8 и mx>1:
>0.8 и mx>1:
hw/tw≤(0.36+0.8*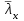 )*(E/Ry)0.5,
)*(E/Ry)0.5,
hw/tw≤(0.36+0.8*2.51)*(206000/240)0.5=69.3,
tw≥hw/69.3=664/69.3=9.6 мм.
Принимаем толщину стенки tw=11 мм.
Требуемая площадь полки:
Аf.тр=(Атр-tw*hw)/2,
Аf.тр=(16030-10*664)/2=4695 мм2.
Задаемся шириной полки из условия устойчивости верхней части колонны из плоскости действия момента:
bf≥ly2/20,
bf≥5400/20=270 мм, примем bf=280 мм.
Условие местной устойчивости полки:
bсв/tf≤(0.36+0.1* )*(E/Ry)0.5,
)*(E/Ry)0.5,
где bсв=(bf-tw)/2=(280-10)/2=135, тогда
bсв/tf≤(0.36+0.1*2.51)*(206000/240)0.5=17.9, тогда
tf≥bсв/17.9=135/17.9=7.5 мм.
Принимаем сечение части колонны –двутавр с размерами:
bf=400 мм;
tf=16,5 мм;
Аf=280*18=5040 мм2>Аf.тр=4695 мм2;
hw=393 мм;
tw=11 мм;
Аw=664*10=6640 мм2.
Геометрические характеристики сечения.
Полная площадь сечения:
А0=2*Аf+Аw,
А0=2*5040+6640=16720 мм2.
Моменты инерции сечения относительно осей х и y:
Ix=tw*hw3/12+2*bf*tf*[(hв-tf)/2]2,
Iy=2*tf*bf3/12.
Ix=10*6643/12+2*280*18*[(700-18)/2]2=1416074933 мм4,
Iy=2*18*2803/12=65856000 мм4.
Момент сопротивления сечения относительно оси х:
Wx=Ix/(0.5*hв),
Wx=1416074933/(0.5*700)=4045928 мм3.
ρx=Wx/А0=4045928/16720=242 мм.
Радиусы инерции сечения относительно осeй х и y:
ix=(Ix/А0)0,5,
iy=(Iy/А0)0,5.
ix=(1416074933/16720)0,5=291 мм,
iy=(65856000/16720)0,5=63 мм.
Проверка устойчивости колонны в плоскости действия момента.
Расчет на устойчивость внецентренно-сжатого элемента постоянного сечения в плоскости действия момента выполняем по формуле:
N1/(φe*A0)≤Ry*γc,
φe – коэффициент определяемый по табл. 74 СНиП II-23-81* и зависящий от условной гибкости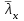 =λx*(Ry/E)0.5 и приведенного относительного эксцентриситета mеf определяемого по формуле:
=λx*(Ry/E)0.5 и приведенного относительного эксцентриситета mеf определяемого по формуле:
mef x=η*mx,
где η – коэффициент влияния формы сечения, определяемый по табл. 73 СНиП II-23-81*,
mx=Mx/(N1*ρx) – относительный эксцентриситет.
λx=lx2/ix=21600/291=74.2.
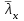 =74.2*(240/206000)0.5=2.53, 0<
=74.2*(240/206000)0.5=2.53, 0<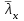 <5
<5
mx=765.853*103/(646.32*242)=4.90.
Аf/Аw=5040/6640=0.76≈0.5.
Коэффициент влияния формы сечения:
η=(1,75-0,1*mx)-0,02*(5-mx)*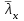 ,
,
η=(1,75-0,1*4.90)-0,02*(5-4.90)*2.53=1.26.
mef x=1.26*4.90=6.15.
По таблице 74 СНиП II-23-81* находим φe=0.173.
σ=646.32/(0.173*240)=223.4 МПа < Ry=240 МПа.
Недонапряжение:
∆=100*(240-223.4)/240=6.9 %.
Проверка устойчивости колонны из плоскости действия момента.
Расчет на устойчивость внецентренно-сжатых элементов постоянного сечения из плоскости действия момента выполняем по формуле:
N1/(с*φy*A0)≤Ry*γc,
где φy – коэффициент определяемый по табл. 72 СНиП II-23-81*.
Определим коэффициенты с и φy.
λy=ly2/iy=5400/63=86, по табл. 72 СНиП II-23-81* находим φy=0.640.
Максимальный момент в средней трети расчетной длины стержня:
Mx1/3=M2+(l2-ly2/3)*(M1-M2)/l2,
Mx1/3=681.619+(7200-5400/3)*(-765.853-681.619)/7200=-404 кН*м.
IMx1/3I>IМmax/2I=766/2=383 кН*м.
Относительный эксцентриситет:
mx=Mx1/3*A0/(N1*Wx),
mx=-404*16720/(646.32*4045928)=2.58.
При mx<5 коэффициент с, учитывающий влияние момента Мх при изгибно-крутильной форме, вычисляется по формуле:
с=β/(1+α*mx),
λy=86<λс=3.14*(E/Ry)0.5=3.14*(206000/240)0.5
Коэффициент расчетной длины в плоскости X1OY1 1
Расстояние между точками раскрепления из плоскости изгиба 2,669 м
Сечение

Профиль: Уголок равнополочный по ГОСТ 8509-93 L140x10
| Результаты расчета | Проверка | Коэффициент использования |
| п.9.1.1 | Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики | 0,13 |
| п.7.1.3 | Устойчивость при сжатии в плоскости XOY (XOU) | 0,15 |
| п.7.1.3 | Устойчивость при сжатии в плоскости XOZ (XOV) ) | 0,17 |
| п.7.1.1 | Прочность при центральном сжатии/растяжении | 0,13 |
| п.10.4.1 | Предельная гибкость в плоскости XOY | 0,28 |
| п.10.4.1 | Предельная гибкость в плоскости XOZ | 0,41 |
Коэффициент использования 0,41 - Предельная гибкость в плоскости XOZ
Конструктивная группа Раскосы. Элемент № 43
Сталь: C245
Длина элемента 2,28 м
Предельная гибкость для сжатых элементов: 180 - 60
Предельная гибкость для растянутых элементов: 400
Коэффициент условий работы 1
Коэффициент надежности по ответственности 1
Неупругая работа сечения не допускается
Коэффициент расчетной длины в плоскости X1OZ1 1
Коэффициент расчетной длины в плоскости X1OY1 1
Расстояние между точками раскрепления из плоскости изгиба 2,282 м
Сечение
 Профиль: Уголок равнополочный по ГОСТ 8509-93 L110x8
Профиль: Уголок равнополочный по ГОСТ 8509-93 L110x8| Результаты расчета | Проверка | Коэффициент использования |
| п.8.2.1 | Прочность при действии изгибающего момента My | 0,39 |
| п.8.2.1 | Прочность при действии поперечной силы Qz | 0,01 |
| п.9.1.1 | Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики | 0,77 |
| п.7.1.1 | Прочность при центральном сжатии/растяжении | 0,39 |
| п.10.4.1 | Предельная гибкость в плоскости XOY | 0,11 |
| п.10.4.1 | Предельная гибкость в плоскости XOZ | 0,17 |
Коэффициент использования 0,77 - Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики
Конструктивная группа Стойки. Элемент № 35
Сталь: C245
Длина элемента 2,89 м
Предельная гибкость для сжатых элементов: 180 - 60
Предельная гибкость для растянутых элементов: 400
Коэффициент условий работы 1
Коэффициент надежности по ответственности 1
Неупругая работа сечения не допускается
Коэффициент расчетной длины в плоскости X1OZ1 1
Коэффициент расчетной длины в плоскости X1OY1 1
Расстояние между точками раскрепления из плоскости изгиба 2,889 м
Сечение

Профиль: Уголок равнополочный по ГОСТ 8509-93 L90x8
| Результаты расчета | Проверка | Коэффициент использования |
| п.9.1.1 | Прочность при совместном действии продольной силы и изгибающих моментов без учета пластики | 0,05 |
| п.7.1.3 | Устойчивость при сжатии в плоскости XOY (XOU) | 0,07 |
| п.7.1.3 | Устойчивость при сжатии в плоскости XOZ (XOV) ) | 0,11 |
| п.7.1.1 | Прочность при центральном сжатии/растяжении | 0,05 |
| п.10.4.1 | Предельная гибкость в плоскости XOY | 0,45 |
| п.10.4.1 | Предельная гибкость в плоскости XOZ | 0,7 |
Коэффициент использования 0,7 - Предельная гибкость в плоскости XOZ
3.5 Расчет колонны
3.5.1 Подбор сечения колонны
Колонна сплошного сечения выполнена из прокатного широкополочного двутавра, высотой 8 м. Имеет шарнирное сопряжение с фермой, и жесткое - с фундаментом. Материал колонны – сталь С235, бетон фундамента В20.
Так как колонна имеет сплошное сечение, то принимаем двутавр высотой hв=400 мм (рисунок 20).
Для симметричного двутавра:
i
 x≈0,42*hв, Рисунок 3.11 Сечение колонны
x≈0,42*hв, Рисунок 3.11 Сечение колонныρх≈0,35*hв.
ix≈0,42*400=294 мм;
ρх≈0,35*400=245 мм.
Условная гибкость:
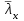 =(lx2/ix)*(Ry/E)0.5,
=(lx2/ix)*(Ry/E)0.5,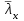 =(21600/294)*(240/206000)0.5=2.51.
=(21600/294)*(240/206000)0.5=2.51. Относительный эксцентриситет:
mx=ex/ρx=M1/(N1*ρx),
mx=765.853*103/(646.32*245)=4.84.
Примем в первом приближении Аf/Аw=1, тогда коэффициент влияния формы сечения:
η=(1.90-0.1*mx)-0.02*(6-mx)*
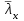 ,
,η=(1.90-0.1*4.84)-0.02*(6-4.84)*2.51=1.36.
Приведенный относительный эксцентриситет:
mx ef=η*mx,
mx ef=1.36*4.84=6.57.
По таблице 74 СП II-23-81* находим φе=0.168.
Компоновка сечения.
Принимаем толщину полок tf=16,5 мм.
Высота стенки:
hw=hв-2*tf,
hw=700-2*18=664 мм.
Условие местной устойчивости стенки при
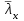 >0.8 и mx>1:
>0.8 и mx>1:hw/tw≤(0.36+0.8*
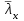 )*(E/Ry)0.5,
)*(E/Ry)0.5,hw/tw≤(0.36+0.8*2.51)*(206000/240)0.5=69.3,
tw≥hw/69.3=664/69.3=9.6 мм.
Принимаем толщину стенки tw=11 мм.
Требуемая площадь полки:
Аf.тр=(Атр-tw*hw)/2,
Аf.тр=(16030-10*664)/2=4695 мм2.
Задаемся шириной полки из условия устойчивости верхней части колонны из плоскости действия момента:
bf≥ly2/20,
bf≥5400/20=270 мм, примем bf=280 мм.
Условие местной устойчивости полки:
bсв/tf≤(0.36+0.1*
 )*(E/Ry)0.5,
)*(E/Ry)0.5,где bсв=(bf-tw)/2=(280-10)/2=135, тогда
bсв/tf≤(0.36+0.1*2.51)*(206000/240)0.5=17.9, тогда
tf≥bсв/17.9=135/17.9=7.5 мм.
Принимаем сечение части колонны –двутавр с размерами:
bf=400 мм;
tf=16,5 мм;
Аf=280*18=5040 мм2>Аf.тр=4695 мм2;
hw=393 мм;
tw=11 мм;
Аw=664*10=6640 мм2.
Геометрические характеристики сечения.
Полная площадь сечения:
А0=2*Аf+Аw,
А0=2*5040+6640=16720 мм2.
Моменты инерции сечения относительно осей х и y:
Ix=tw*hw3/12+2*bf*tf*[(hв-tf)/2]2,
Iy=2*tf*bf3/12.
Ix=10*6643/12+2*280*18*[(700-18)/2]2=1416074933 мм4,
Iy=2*18*2803/12=65856000 мм4.
Момент сопротивления сечения относительно оси х:
Wx=Ix/(0.5*hв),
Wx=1416074933/(0.5*700)=4045928 мм3.
ρx=Wx/А0=4045928/16720=242 мм.
Радиусы инерции сечения относительно осeй х и y:
ix=(Ix/А0)0,5,
iy=(Iy/А0)0,5.
ix=(1416074933/16720)0,5=291 мм,
iy=(65856000/16720)0,5=63 мм.
3.5.2 Проверка устойчивости колонны
Проверка устойчивости колонны в плоскости действия момента.
Расчет на устойчивость внецентренно-сжатого элемента постоянного сечения в плоскости действия момента выполняем по формуле:
N1/(φe*A0)≤Ry*γc,
φe – коэффициент определяемый по табл. 74 СНиП II-23-81* и зависящий от условной гибкости
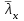 =λx*(Ry/E)0.5 и приведенного относительного эксцентриситета mеf определяемого по формуле:
=λx*(Ry/E)0.5 и приведенного относительного эксцентриситета mеf определяемого по формуле:mef x=η*mx,
где η – коэффициент влияния формы сечения, определяемый по табл. 73 СНиП II-23-81*,
mx=Mx/(N1*ρx) – относительный эксцентриситет.
λx=lx2/ix=21600/291=74.2.
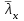 =74.2*(240/206000)0.5=2.53, 0<
=74.2*(240/206000)0.5=2.53, 0<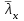 <5
<5mx=765.853*103/(646.32*242)=4.90.
Аf/Аw=5040/6640=0.76≈0.5.
Коэффициент влияния формы сечения:
η=(1,75-0,1*mx)-0,02*(5-mx)*
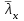 ,
,η=(1,75-0,1*4.90)-0,02*(5-4.90)*2.53=1.26.
mef x=1.26*4.90=6.15.
По таблице 74 СНиП II-23-81* находим φe=0.173.
σ=646.32/(0.173*240)=223.4 МПа < Ry=240 МПа.
Недонапряжение:
∆=100*(240-223.4)/240=6.9 %.
Проверка устойчивости колонны из плоскости действия момента.
Расчет на устойчивость внецентренно-сжатых элементов постоянного сечения из плоскости действия момента выполняем по формуле:
N1/(с*φy*A0)≤Ry*γc,
где φy – коэффициент определяемый по табл. 72 СНиП II-23-81*.
Определим коэффициенты с и φy.
λy=ly2/iy=5400/63=86, по табл. 72 СНиП II-23-81* находим φy=0.640.
Максимальный момент в средней трети расчетной длины стержня:
Mx1/3=M2+(l2-ly2/3)*(M1-M2)/l2,
Mx1/3=681.619+(7200-5400/3)*(-765.853-681.619)/7200=-404 кН*м.
IMx1/3I>IМmax/2I=766/2=383 кН*м.
Относительный эксцентриситет:
mx=Mx1/3*A0/(N1*Wx),
mx=-404*16720/(646.32*4045928)=2.58.
При mx<5 коэффициент с, учитывающий влияние момента Мх при изгибно-крутильной форме, вычисляется по формуле:
с=β/(1+α*mx),
λy=86<λс=3.14*(E/Ry)0.5=3.14*(206000/240)0.5