ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 79
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
ФГБОУ ВО «ДАЛЬНЕВОСТОЧНЫЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»
Кафедра «Информационные
технологии и системы»
Курсовой проект
по дисциплине «Интеллектуальные информационные системы»
на тему: «Разработка искусственной нейронной сети»
Вариант «Арабские цифры»
Выполнил: Сазанова Е.В.
Группа ИБ2
Проверил: Ешенко Р.А.
Хабаровск
2018
Оглавление
Задание на выполнение курсового проекта 3
Введение 4
1.Основные параметры и структура нейронной сети 7
2.Эталонные образы для обучения нейронной сети 8
3. Алгоритм обратного распространения ошибки 9
3.1 Процедура обучения 9
3.2 Результаты распознавания контрольных образов 10
4. Оценка влияния параметров нейронной сети на качество распознавания образов 20
5. Выбор оптимальных параметров нейронной сети 21
6. Руководство пользователя 21
Заключение 22
Список используемых источников 23
Задание на выполнение курсового проекта
Разработать программу для распознавания образов на базе искусственной нейронной сети.
Тип сети - с прямыми связями.
Алгоритм обучения сети - с обратным распространением ошибки.
Количество эпох (повторов обучения всем эталонным образцам) - 1000.
Исследовать влияние типа функции активации, структуры сети и нормы обучения на качество распознавания образов:
- функция активации: сигмоидальная, гиперболический тангенс, арктангенс;
- количество скрытых слоев: 0, 1, 2;
- норма обучения: 0.01, 0.05, 0.1.
Введение
Одним из наиболее эффективных и распространенных способов представления и решения типов задач распознавания образов являются искусственные нейронные сети (ИНС).
Обобщенная математическая модель нейрона выглядит следующим образом (рис. 1):
-
входные сигналы xi – это данные, поступающие из окружающей среды или от других активных нейронов. Входные значения могут быть дискретными из множеств [0, 1] или [-1, 1] либо принимать любые вещественные значения. -
вещественные весовые коэффициенты wi – определяют силу связи между нейронами; -
уровень активации (потенциал) нейрона P = wi xi; -
функция активации Y = f(P) – предназначена для вычисления выходного значения сигнала, передаваемого другим нейронам.
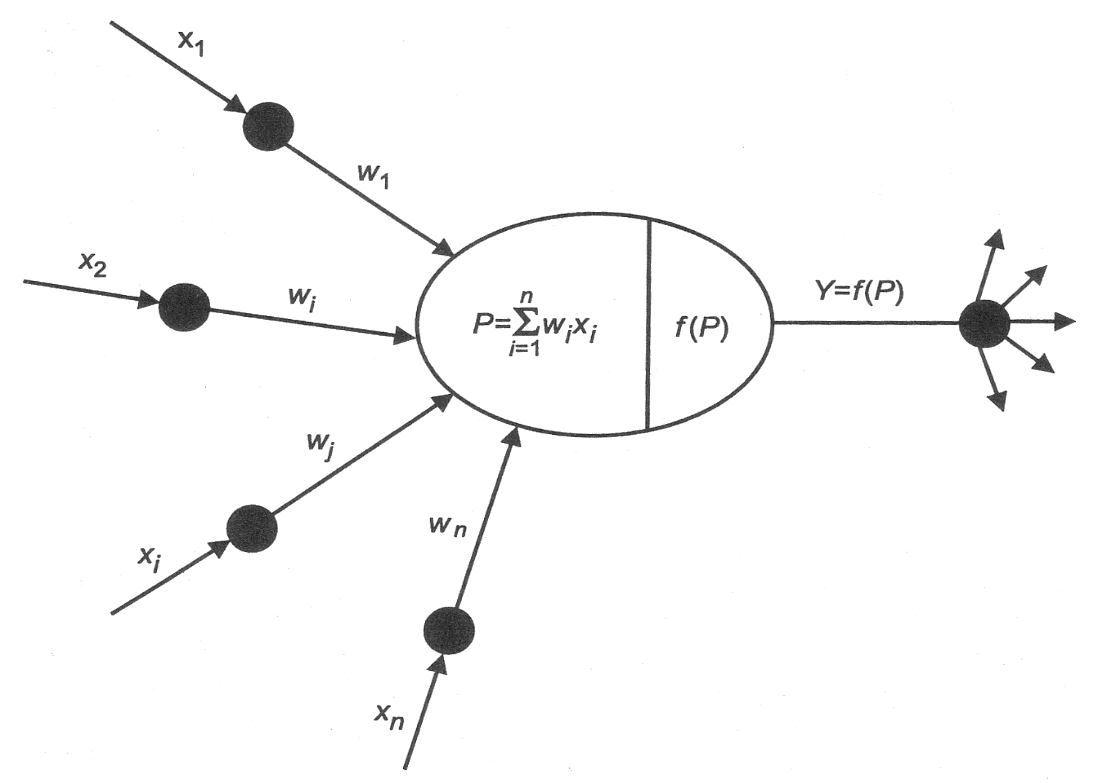
Рис. 1
Перед непосредственным использованием, т.е. перед решением конкретной задачи распознавания образов, необходимо настроить (обучить) сеть.
Первым этапом построения нейросетевой модели является тщательный отбор входных данных, влияющих на ожидаемый результат. Из исходной информации необходимо исключить все сведения, не относящиеся к исследуемой проблеме. В то же время следует располагать достаточным количеством примеров для обучения ИНС. Существует эмпирическое правило, которое устанавливает рекомендуемое соотношение между количеством обучающих примеров, содержащих входные данные и правильные ответы, и числом соединений в нейронной сети: 10.
Для факторов, которые включаются в обучающую выборку, целесообразно предварительно оценить их значимость, проведя корреляционный и регрессионный анализ, и проанализировать диапазоны их возможных изменений.
На втором этапе осуществляется преобразование исходных данных с учетом характера и типа проблемы, отображаемой нейросетевой моделью, и выбираются способы представления информации. Эффективность нейросетевой модели повышается, если диапазоны изменения входных и выходных величин приведены к некоторому стандарту, например, [0,1] или [-1,1].
Третий этап заключается в проектировании архитектуры ИНС (определение числа слоев и числа нейронов в каждом слое) и выборе функции активации нейронов, учитывающей характер решаемой задачи. Структура ИНС формируется до начала обучения, поэтому успешное решение этой проблемы во многом определяется опытом и искусством аналитика, проводящего исследования.
Четвертый этап связан с обучением сети - уточнением значений весовых коэффициентов связей на основе многократного прогона через сеть тестовых примеров. Третий и четвертый этапы могут совместно применяться для уточнения структуры сети на основе конструктивного или деструктивного подхода. В соответствии с первым подходом обучение ИНС начинается на сети небольшого размера, который постепенно увеличивается до достижения требуемой точности по результатам тестирования. Деструктивный подход базируется на принципе «прореживания дерева», в соответствии с которым из сети с заведомо избыточным объемом постепенно удаляют «лишние» нейроны и примыкающие к ним связи. Этот подход дает возможность исследовать влияние удаленных связей на точность сети.
На пятом этапе проводится тестирование полученной модели ИНС на независимой выборке примеров.
В данном проекте разработана программа для распознавания образов на базе искусственной нейронной сети. Исследовано влияние типа функции активации, структуры сети и алгоритмов обучения на качество распознавания образов:
-
функции активации: сигмоидальная, гиперболический тангенс, арктангенс; -
количество скрытых слоев: 0, 1, 2; -
количество эпох обучения: 500, 1000; -
норма обучения: 0.01, 0.05, 0.1.
-
Основные параметры и структура нейронной сети
Исходный образ можно представить матрицей 9х9. В данном проекте исходными образами для нейронной сети являются арабские цифры.
Таким образом, количество элементов входного слоя равно 81 (9*9). На вход этим элементам поступают значения либо 0 (белая клетка), либо 1 (черная клетка).
Количество элементов выходного слоя равно количеству распознаваемых образов, т.е. 10 штук.
В проекте рассмотрена сеть с количеством скрытых слоев 0, 1 и 2.
В данном проекте рассмотрена работа нейронной сети при трех различных функциях активации:
- сигмоидальная функция Y = 1 / (1 + e-aP)
- гиперболический тангенс Y = a th(b P) = a (ebP – e-bP) / (ebP + e-bP)
- арктангенс Y = 2 arctg(P) / , где P = wi xi – уровень активации (потенциал) нейрона.
Каждый выходной нейрон
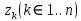 изменяет веса своих связей с элементом смещения и скрытыми нейронами:
изменяет веса своих связей с элементом смещения и скрытыми нейронами: 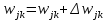 . Каждый скрытый нейрон
. Каждый скрытый нейрон 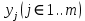 изменяет веса своих связей с элементом смещения и скрытыми нейронами:
изменяет веса своих связей с элементом смещения и скрытыми нейронами: 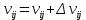 .
.Норма обучения – коэффициент, от которого зависит величина изменения веса (скорость обучения). Выбирается в диапазоне 0 < < 1. В данном проекте согласно заданию рассмотрены случаи с нормой обучения 0.01, 0.05 и 0.1.
Количество эпох – повторов обучения всем эталонным образцам. В данном проекте рассмотрены варианты с количеством эпох равным 500 и 1000.
-
Эталонные образы для обучения нейронной сети
Перед непосредственным использованием, т.е. перед решением конкретной задачи распознавания образов, необходимо настроить (обучить) сеть. Процесс обучения сети заключается в определении набора связей и коэффициентов связей между нейронами. В зависимости от способа обучения различают следующие типы ИНС:
• обучаемые с учителем (контролируемое или наблюдаемое обучение). При обучении с учителем все примеры обучающей выборки содержат правильные ответы (выходы), соответствующие исходным данным (входам). В процессе обучения веса (коэффициенты) настраиваются так, чтобы сеть порождала ответы, наиболее близкие к правильным;
• обучаемые без учителя (неконтролируемое или ненаблюдаемое обучение). Обучение без учителя используется, когда не для всех примеров обучающей выборки известны правильные ответы. В этом случае предпринимаются попытки определения коэффициентов сети с целью определения категорий (классов) образцов и дальнейшего их распределения по категориям. Используется, в частности, для решения задач кластеризации;
• со смешанным (гибридное) обучением. При смешанном обучении часть весов определяется посредством обучения с учителем, а другая часть получается с помощью алгоритмов самообучения.
В рамках выполнения данной работы будет создана ИНС, обучение которой будет проводиться с участием учителя (пользователя). Для проведения обучения нейронной сети необходимо наличие совокупности образов, называемых эталонными образцами. Именно их нейронная сеть будет распознавать на каждом этапе своего обучения. Согласно варианту, в качестве эталонных образцов были выбраны арабские цифры. Вид эталонных образцов представлен на рис.2.
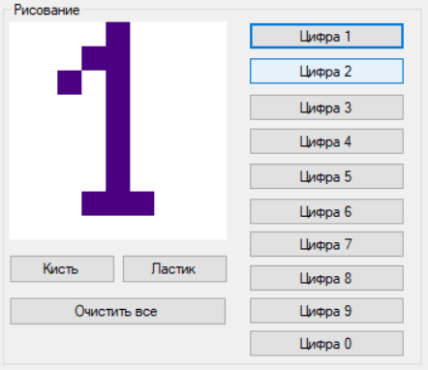









Рис. 2
3. Алгоритм обратного распространения ошибки
3.1 Процедура обучения
Алгоритм подразумевает два потока сигналов (данных) при прогоне одного обучающего образа через сеть:
-
прямой (от входного до выходного слоя) распространение сигнала, соответствующего значениям входного вектора обучающего образа; -
обратный (от выходного до входного слоя) распространение сигнала ошибки для корректировки весовых коэффициентов связей.
Блок-схема алгоритма обратного распространения (рис. 3) представлена ниже.
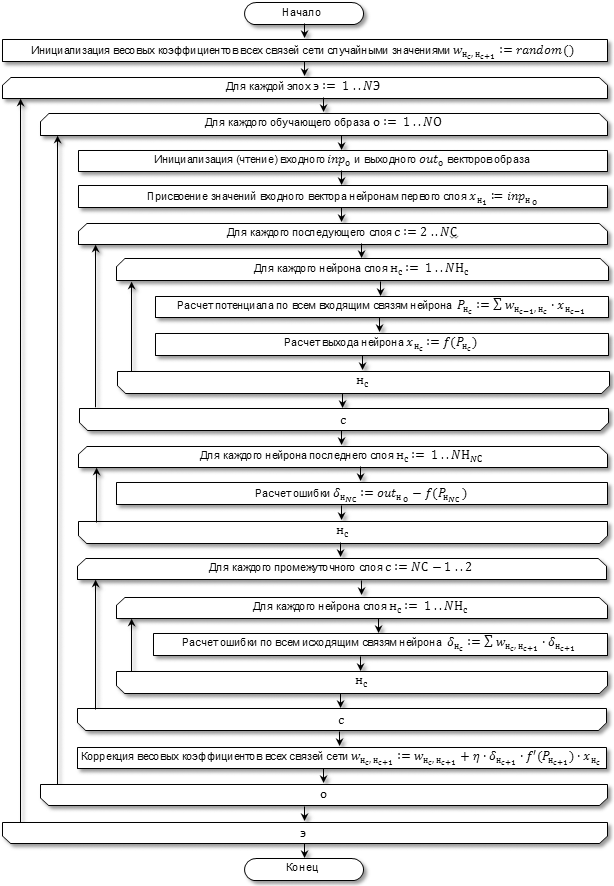
Рис. 3
На рисунке приняты следующие обозначения:
-
э – номер эпохи; -
о – номер обучающего образа; -
с – номер слоя; -
нс – номер нейрона в слое с; -
NЭ – количество эпох; -
NО – количество обучающих образов; -
NС – количество слоев; -
NНс – количество нейронов в слое с; -
inpо – вектор входных значений обучающего образа о; -
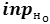 – значение элемента н входного вектора обучающего образа о;
– значение элемента н входного вектора обучающего образа о; -
outо – вектор ожидаемых выходных значений обучающего образа о; -
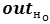 – значение элемента н выходного вектора обучающего образа о;
– значение элемента н выходного вектора обучающего образа о; -
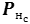 – потенциал нейрона н слоя с;
– потенциал нейрона н слоя с; -
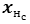 – выход нейрона н слоя с. Для нейронов входного слоя равен соответствующему элементу вектора входных значений
– выход нейрона н слоя с. Для нейронов входного слоя равен соответствующему элементу вектора входных значений 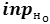 , для остальных слоев – результату расчета функции активации
, для остальных слоев – результату расчета функции активации 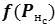 ;
; -
wi,j – весовой коэффициент связи нейрона i предыдущего слоя и нейрона j последующего слоя; -
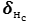 – ошибка (сигнал ошибки) нейрона н слоя с;
– ошибка (сигнал ошибки) нейрона н слоя с; -
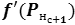 – результат расчета первой производной функции активации нейрона н слоя с+1;
– результат расчета первой производной функции активации нейрона н слоя с+1; -
η – норма обучения.