Файл: Разработка искусственной нейронной сети.docx

Рис. 4
В качестве образа для теста для получения более точных результатов была выбрана зашумленная цифра «2» (Рис. 4). Результаты тестов при разных конфигурациях сети представлены в таблице. Результаты распознавания без указания распознанной цифры являются распознаванием без ошибки.

№	Функция активации	Норма обучения	Количество скрытых слоев	Количество эпох	Результат распознавания
2	Сигмоидальная	0,01	0	500
3	Сигмоидальная	0,01	0	1000
4	Сигмоидальная	0,01	1	500
5	Сигмоидальная	0,01	1	1000
6	Сигмоидальная	0,01	2	500
7	Сигмоидальная	0,01	2	1000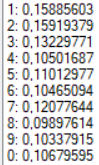
8	Сигмоидальная	0,05	0	500
9	Сигмоидальная	0,05	0	1000
10	Сигмоидальная	0,05	1	500
11	Сигмоидальная	0,05	1	1000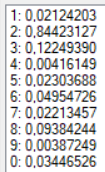
12	Сигмоидальная	0,05	2	500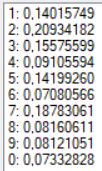
13	Сигмоидальная	0,05	2	1000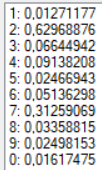
14	Сигмоидальная	0,1	0	500
15	Сигмоидальная	0,1	0	1000
16	Сигмоидальная	0,1	1	500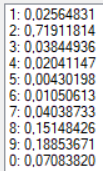
17	Сигмоидальная	0,1	1	1000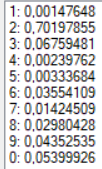
18	Сигмоидальная	0,1	2	500
19	Сигмоидальная	0,1	2	1000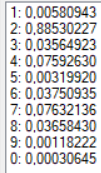
20	Гиперболический тангенс	0,01	0	500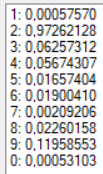
21	Гиперболический тангенс	0,01	0	1000
22	Гиперболический тангенс	0,01	1	500
23	Гиперболический тангенс	0,01	1	1000
24	Гиперболический тангенс	0,01	2	500
25	Гиперболический тангенс	0,01	2	1000
26	Гиперболический тангенс	0,05	0	500
27	Гиперболический тангенс	0,05	0	1000
28	Гиперболический тангенс	0,05	1	500
29	Гиперболический тангенс	0,05	1	1000
30	Гиперболический тангенс	0,05	2	500
31	Гиперболический тангенс	0,05	2	1000
32	Гиперболический тангенс	0,1	0	500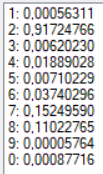
33	Гиперболический тангенс	0,1	0	1000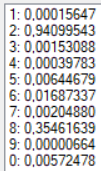
34	Гиперболический тангенс	0,1	1	500
35	Гиперболический тангенс	0,1	1	1000
36	Гиперболический тангенс	0,1	2	500
37	Гиперболический тангенс	0,1	2	1000
38	Арктангенс	0,01	0	500
39	Арктангенс	0,01	0	1000
40	Арктангенс	0,01	1	500
41	Арктангенс	0,01	1	1000
42	Арктангенс	0,01	2	500
43	Арктангенс	0,01	2	1000
44	Арктангенс	0,05	0	500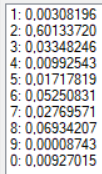
45	Арктангенс	0,05	0	1000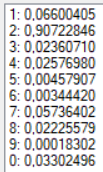
46	Арктангенс	0,05	1	500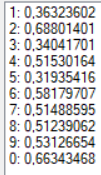
47	Арктангенс	0,05	1	1000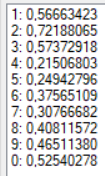
48	Арктангенс	0,05	2	500
49	Арктангенс	0,05	2	1000
50	Арктангенс	0,1	0	500
51	Арктангенс	0,1	0	1000
52	Арктангенс	0,1	1	500
53	Арктангенс	0,1	1	1000
54	Арктангенс	0,1	2	500
55	Арктангенс	0,1	2	1000

4. Оценка влияния параметров нейронной сети на качество распознавания образов

Сигмоидальная функция является наиболее подходящей для обучения нейронной сети. При различном количестве слоев, норме обучения и количестве эпох дает меньше всего ошибок при тестировании обученной сети с помощью контрольных образов и с помощью образов, содержащих помехи.

Худшие результаты показала функция арктангенс. Она дала наименьший показатель правильных ответов при тестировании на образах с помехами.

Функция гиперболический тангенс дает лучшие результаты по времени обучения, но при количестве скрытых слоев равном 1, встречаются ошибки при тестировании контрольных образцов, а при количестве скрытых слоев равном 2 ошибки встречаются в 90% случаев.

Количество скрытых слоев существенно повлияло на качество работы нейронной сети не только в случае гиперболического тангенса. В рассмотренных примерах лучшим образом себя показали конфигурации однослойной (без скрытых слоев) ИНС. Это связано с тем, что для качественного обучения многослойных нейронных сетей требуется либо еще больше увеличить норму обучения, либо многократно увеличить количество эпох обучения.

Качество распознавания образов увеличивается при увеличении количественной характеристики нормы обучения, а также при увеличении количества эпох обучения. В таблице, представленной выше, наглядно показано, что при конфигурациях ИНС, идентичных друг другу во всем, кроме этой составляющей, качество распознавания образов лучше там, где норма обучения больше

5. Выбор оптимальных параметров нейронной сети

Исходя из результатов анализа, описанных выше, оптимальной функцией активации является сигмоидальная при количестве скрытых слоев равном 0 или 1. При увеличении количества слоев необходимо будет увеличивать норму обучения и количество эпох. Оптимальной нормой обучения является показатель 0,05 при количестве эпох 1000 или показатель нормы обучения 0,1 при количестве эпох 500-1000.

6. Руководство пользователя

Окно программы (рис. 5) выглядит следующим образом:

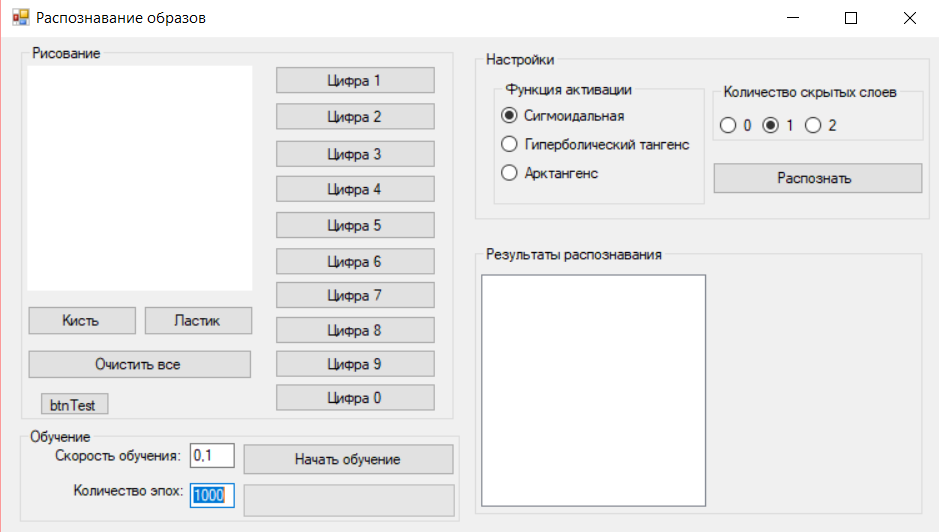
Рис. 5
Для обучения сети необходимо установить параметры для обучения. Выбрать количество скрытых слоев, функцию активации, режим обучения (норму обучения, количество эпох) и нажать кнопку «Начать обучения». Процесс обучения занимает некоторое время и отображается на прогресс баре под кнопкой.

Для просмотра эталонных образцов имеются кнопки, отображающие каждый из них на панели для рисования. Для тестирования образцов можно выбрать цифру из списка и нажать на неё, а после внести в рисунок изменения путем нажатия на кнопку «Кисть», а затем рисования на панели. При необходимости стереть часть рисунка можно нажать на кнопку «Ластик». Если нужно стереть рисунок полностью, можно нажать на кнопку «Очистить все». Кнопка «btnTest» загружает рисунок, с помощью которого производились тесты.

После того, как сеть обучена, а рисунок для распознавания загружен, необходимо нажать на кнопку «Распознать». Результаты распознавания отобразятся в блоке «Результаты распознавания» (рис. 6).

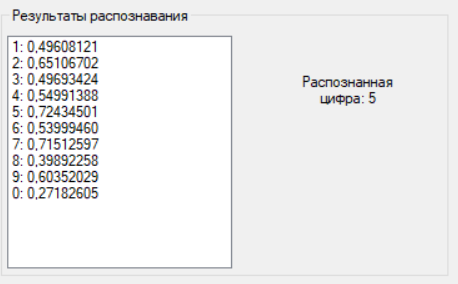
Рис. 6

Заключение

В ходе выполнения курсового проекта была разработана искусственная нейронная сеть с прямыми связями, обучение которой реализовано с помощью алгоритма обратного распространения ошибки. Сеть обучена распознавать фигуры (круг, треугольник, плюсик, крестик, квадрат).

В рамках работы был проведен анализ работы искусственной нейронной сети при использовании трех видов функций активации: сигмоидальная, гиперболический тангенс и арктангенс. Для каждой из функций применялись различное количество скрытых слоев (0, 1, 2).

В результате оценки работы сети сделаны выводы об оценке влияния функции активации, количества скрытых слоев и нормы обучения на качество распознавания образов, а также выбраны оптимальные параметры для данной нейронной сети.

Список используемых источников

Википедия. Свободная энциклопедия [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org
Искусственные нейронные сети: Методические материалы для выполнения курсового проекта/ В.В. Анисимов; ДВГУПС, 2011г.
И. В. Заенцев. Нейронные сети: основные модели. Учебное пособие к курсу “Нейронные сети”
Портал Искусственного интеллекта Aiportal.ru [Электронный ресурс]. – Режим доступа: http://aiportal.ru
Ф. Уоссермен. Нейрокомпьютерная техника: теория и практика. Перевод на русский язык Ю. А. Зуев, В. А. Точенов, 1992
Хайкин С. Нейронные сети: полный курс. 2-е изд. Москва, 2008.