Файл: 1 Численные методы решения нелинейных алгебраических уравнений 3.docx

Содержание

Введение

Под численными методами подразумеваются приближенные процедуры, позволяющие получать решение в виде конкретных числовых значений.

В настоящее время численные методы являются мощным математическим средством решения многих научно-технических проблем. Это связано как с невозможностью в большинстве случаев получить точное аналитическое решение, так и со стремительным развитием ЭВМ. Несмотря на существование многочисленных стандартных программ и объектно ориентированных пакетов прикладных программ, для научных и инженерно-технических работников необходимо понимание существа основных численных методов и алгоритмов, поскольку зачастую интерпретация результатов расчетов нетривиальна и требует специальных знаний особенностей применяемых методов. В этой связи важно понимать структуру погрешностей при решении конкретных задач и корректность вычислений.

Целью контрольной работы является получение навыков решения нелинейных уравнений, построения математических моделей, решения систем нелинейных уравнений различными методами.

1 Численные методы решения нелинейных алгебраических уравнений

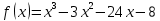
В качестве исходных данных необходимо указать отрезок, содержащий только один корень уравнения, отделить корень. Таким образом, надо найти отрезок [a,b], на котором содержится ровно один корень уравнения f(x)=0.

Для определения отрезка [a,b] воспользуемся графическим методом.

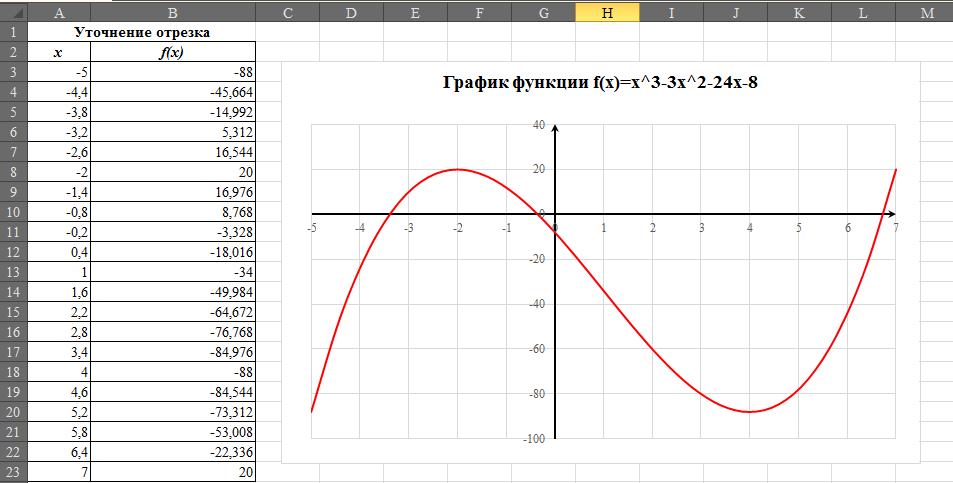
На рабочем листе таблицы Excel протабулируем функцию 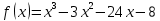на интервале [-5;7], построим график и определим отрезки, на которых функция меняет знак, т.е. пересекает ось OX. На этом отрезке находится корень уравнения, который уточним с помощью численных методов. Функция пересекает ось ОХ на отрезках [-4;-3], [-1;0], [6;7], следовательно, на этом отрезке имеется корень.

---

1.1 Метод половинного деления

Метод деления пополам позволяет исключать в точности половину интервала на каждой итерации. При использовании метода считается, что функция непрерывна и имеет на концах интервала разный знак. После вычисления значения функции в середине интервала одна часть интервала отбрасывается так, чтобы функция имела разный знак на концах оставшейся части. Итерации метода деления пополам прекращаются, если интервал становится достаточно малым.

Словесный алгоритм.

1. 
   Найдем отрезок [a,b]: f(a)f(b)<0.
   
2. 
   Положим c=(a+b)/2.
   
3. 
   Если f(a)f(c)<0, то положим b=c, в противном случае a=c.
   
4. 
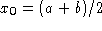   Если  , то 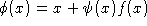 , в противном случае выполнить пункт 2.
   

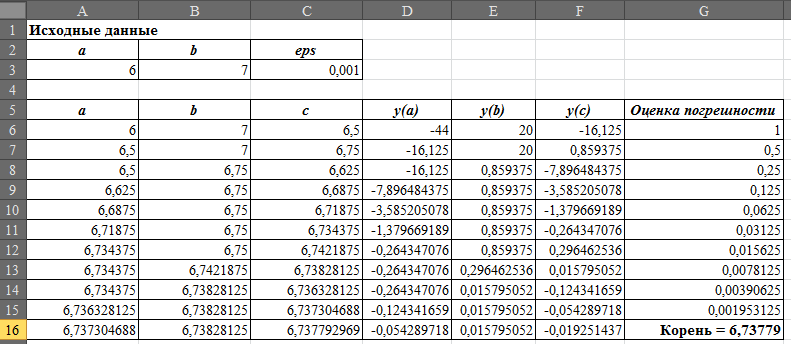
Ответ: корень уравнения на отрезке [6; 7] равен 6,73779.

1.2 Метод хорд

Согласно методу хорд, найденный отрезок [-1,5; 0] делится точкой с, которая находится по формуле , на два отрезка, затем выбираем новый отрезок от точки пересечения хорды с осью абсцисс до неподвижной точки, на которой функция сменяет знак и содержит решение. Полученный отрезок переобозначается [a,b] и снова находится с до тех пор, пока не выполнится условие . За приближенное значение корня принимается с_i+1.



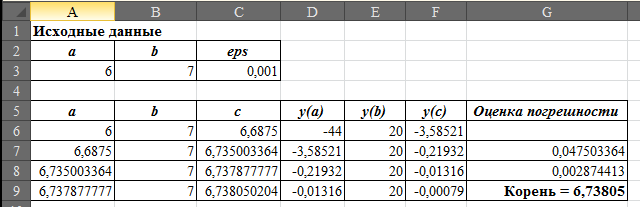
Ответ: корень уравнения на отрезке [6; 7] равен 6,73805.

1.3 Метод касательных

Суть метода касательных состоит в разбиении отрезка [a; b] (при условии f(a)f(b) < 0) на два отрезка с помощью касательной и выборе нового отрезка от точки пересечения касательной с осью абсцисс до неподвижной точки, на котором функция меняет знак и содержит решение, причём подвижная точка приближается к 

---

ε-окрестности решения.

Построение касательных продолжается до достижения необходимой точности решения ε.

Метод касательных применим для решения уравнения вида f(x) = 0 на отрезке [a; b], если ни одна точка отрезка [a; b] не является ни стационарной, ни критической, то есть f’(x) ≠ 0 и f’’(x) ≠ 0.

Условие неподвижной точки для метода касательных f(x)f’’(x) < 0.

Условие начальной точки для метода касательных f(x)f’’(x) > 0.

Сначала находим отрезок [a; b] такой, что функция f(x) дважды непрерывно дифференцируема и меняет знак на отрезке, то есть f(a)f(b) < 0.

Далее применяем алгоритм решения.

Входные данные: f(x), f’(x), f’’(x), a, b, ε.

1. 
   Если f(a)f’’(a) > 0, то x = a, иначе если f(b)f’’(b) > 0, то x = b.
   
2. 
   Δx = f(x)/f’(x).
   
3. 
   x = x − Δx
   
4. 
   Если |Δx| > ε, то идти к 2.
   

Выходные данные: x.

Значение x является решением с заданной точностью ε нелинейного уравнения вида f(x) = 0.

Если f(x) = 0, то x — точное решение.



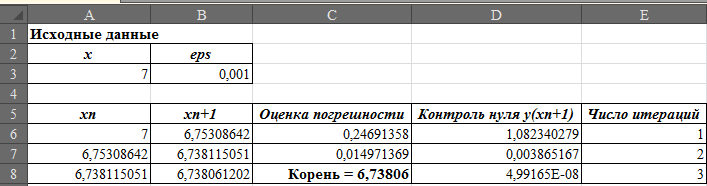
Ответ: корень уравнения на отрезке [6; 7] равен 6,73806.

1.4 Комбинированный метод хорд и касательных

С уть комбинированного метода заключается в приближении к искомому корню одновременно с двух сторон отрезка, на котором отделен корень уравнения. Начальным приближением в методе касательных служит тот конец отрезка, на котором выполняется условие

Тогда приближение по методу касательных будет происходить слева, а по методу хорд – справа.



Ответ: корень уравнения на отрезке [6; 7] равен 6,738.

2 Численные методы решения систем линейных алгебраических уравнений

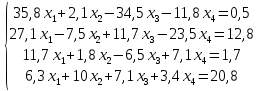
2.1 Метод Гаусса

Суть метода Гаусса состоит в приведении системы уравнений к треугольному виду с помощью элементарных преобразований строк.

Входные данные:  .

---

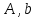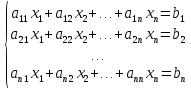
Прямой ход:

, …, , ;

, …, ;

, …, ;

…

, …, ;



, …, , ;

, …, ;

, …, ;

…

, …,

---

;



...

, , ,

, , ,



, ,



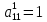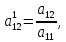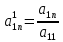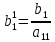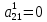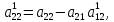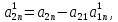
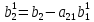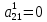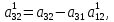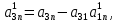
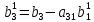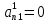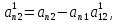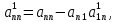
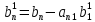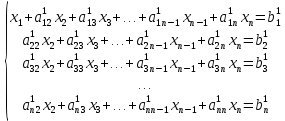
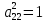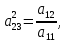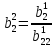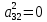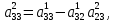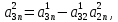
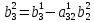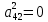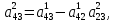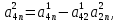
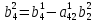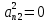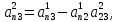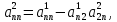
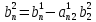
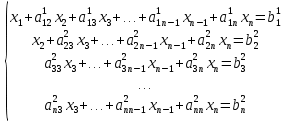
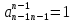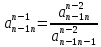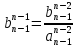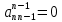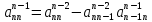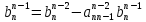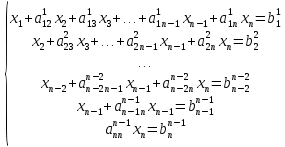
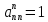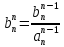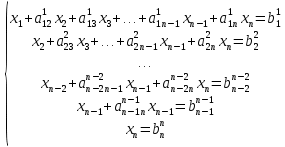
Обратный ход:

,

,

,

…

,

,

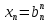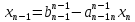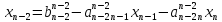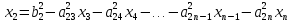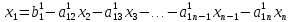Выходные данные: x.



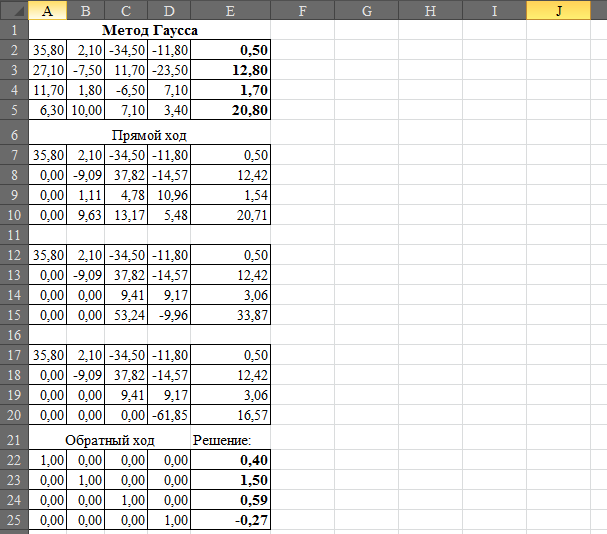
Рисунок 1 Метод Гаусса

Ответ: 0,4; 1,5; 0,59; -0,27.

2.2 Матричный метод (метод обратной матрицы)

Суть метода обратной матрицы состоит в умножении обратной матрицы коэффициентов системы линейных уравнений на вектор свободных членов. Для решения методом обратной матрицы системы линейных уравнений вида Ax=b (где A – квадратная матрица n*n коэффициентов системы, а b – вектор свободных членов системы), сначала найдём главный определитель системы Δ. Метод обратной матрицы применим, если главный определитель системы Δ≠0.



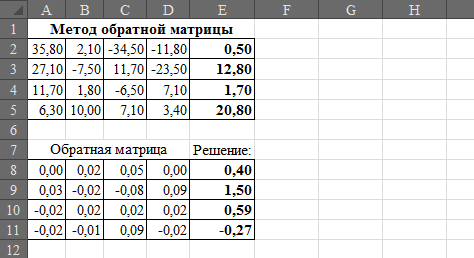
Ответ: 0,4; 1,5; 0,59; -0,27.

3 Методы численного интегрирования

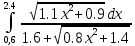
3.1 Метод прямоугольников

Метод прямоугольников – метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке.

---