Файл: 1 Численные методы решения нелинейных алгебраических уравнений 3.docx
Добавлен: 26.10.2023
Просмотров: 128
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пусть функция y = f(x) непрерывна на отрезке [a; b]. Нам требуется вычислить определенный интеграл
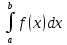.Разобьем отрезок [a;b] на n частей [xi-1;xi] i=1,2,…n точками a=x0
. Так как по определению определенный интеграл есть предел интегральных сумм при бесконечном уменьшении длины элементарного отрезка разбиения 
, то любая из интегральных сумм является приближенным значением интеграла 
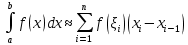.Если отрезок [a,b] является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по формуле левых прямоугольников:
; формуле правых прямоугольников: 
; формуле прямоугольников (средних): 
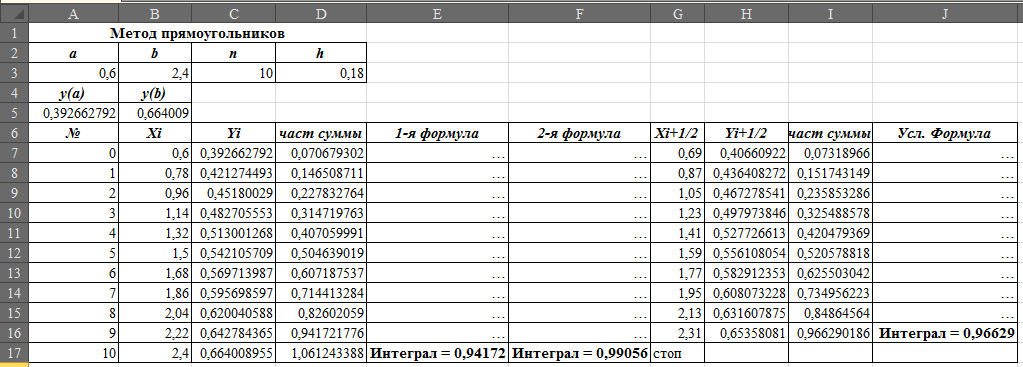
Ответ: интеграл по формуле 1 = 0,94172; по формуле 2 = 0,99056; по усложненной формуле = 0,96629.
3.2 Метод трапеций
Метод трапеций – метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями. Алгебраический порядок точности равен 1.
Если отрезок [a,b] является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по формуле
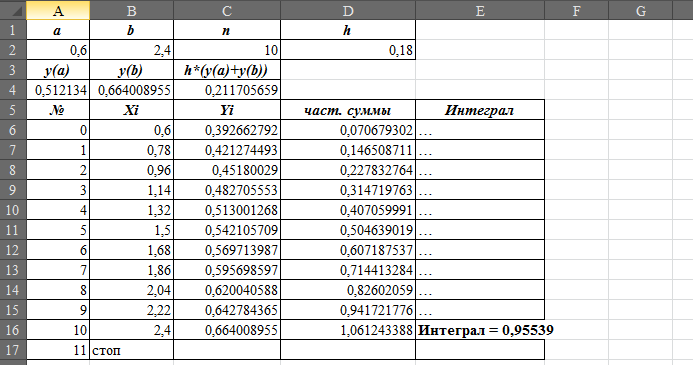
Ответ: интеграл по методу трапеций 0,95539.
Заключение
Численные (вычислительные) методы — методы решения математических задач в численном виде. Многие численные методы являются частью библиотек математических программ. В данной контрольной работе опробованы различные численные методы для решения нелинейных алгебраических уравнений, систем линейных алгебраических уравнений и численного интегрирования.
Таблица 1 Результаты решения
| Численные методы решения нелинейных алгебраических уравнений | |
| Метод дихотомии | 6,73779 |
| Метод хорд | 6,73805 |
| Метод касательных | 6,73806 |
| Комбинированный метод | 6,738 |
| Численные методы решения систем линейных алгебраических уравнений | |
| Метод Гаусса | 0,40; 1,50; 0,59; -0,27 |
| Метод обратной матрицы | 0,40; 1,50; 0,59; -0,27 |
| Методы численного интегрирования | |
| Метод прямоугольников | Интеграл 1 формула = 0,94172 |
| Интеграл 2 формула = 0,99056 | |
| Интеграл Усл формула = 0,96629 | |
| Метод трапеций | Интеграл = 0,95539. |
Список литературы
-
Численные методы / Под ред. Лапчика М.П.. - М.: Academia, 2017. - 608 c. -
Гулин, А.В. Введение в численные методы в задачах и упражнениях: Учебное пособие / А.В. Гулин, В.А. Морозова, О.С. Мажорова. - М.: Инфра-М, 2017. - 432 c. -
Ерохин, Б.Т. Численные методы: Учебное пособие / Б.Т. Ерохин. - СПб.: Лань КПТ, 2016. - 256 c. -
Косарев, В.П. Численные методы линейной алгебры: Учебное пособие / В.П. Косарев, Т.Т. Андрющенко. - СПб.: Лань П, 2016. - 496 c.
c. -
Шахов, Ю.Н. Численные методы / Ю.Н. Шахов, Е.И. Деза. - М.: КД Либроком, 2017. - 248 c.