1. 
   Данные в экономике. Классификация данных.
   

2. 
   Генеральная совокупность и выборка. Суть выборочного метода.
   

Генеральная совокупность Ω – это совокупность всех подлежащих изучению объектов или явлений. В некоторых задачах генеральную совокупность рассматривают как случайную величину Х.

Выборочная совокупность (или выборка) Ω῀ - совокупность случайно отобранных объектов из генеральной совокупности.

• 
  Число объектов совокупности называется объемом совокупности
  
• 
  Объем генеральной совокупности – N
  
• 
  Объем выборки – n
  

Основной метод математической статистики – выборочный. Его суть:

• 
  Выборочный метод – метод матстатистики, где на основе изучения выборки делается заключение обо всей генеральной совокупности.
  
• 
  Теоретической основой применения выборочного метода является Закон Больших Чисел: при неограниченном увеличении объема выборки её характеристики сколь угодно близко приближаются к характеристикам генеральной совокупности.
  

3. 
   Способы осуществления выборки. Условия репрезентативности выборки.
   

Чтобы выборка правильно представляла изучаемый признак генеральной совокупности, хорошо отражала пропорции генеральной совокупности, она должна быть репрезентативной (представительной). Выборка будет репрезентативной, если:

• 
  Её осуществить случайно
  
• 
  Все объекты генеральной совокупности имеют равные вероятности быть отобранными
  

Способы формирования выборки:

• 
  Повторный (возвратный): объект после исследования возвращается в генеральную совокупность
  
• 
  Бесповторный (безвозвратный): объект после исследования не возвращается в генеральную совокупность
  

4. 
   Понятие вариационного ряда. Дискретные и интервальные статистические ряды: понятие, способы задания.
   

Статистический ряд – это ранжированный перечень выриантов xi и соответствующих им весов (частот или частостей)

Общий вид статистического ряда частот/частостей

Значение признака xi	x1	x2	…	xk
Частота ni	n1	n2	…	nk	n1+n2+…+nk=n
Относительная частота ωi	ω1	ω2	…	ωk	ω1+ ω2+…ωk= 1

---

Где k – число различных вариантов в ряду

Статистические ряды бывают дискретными и интервальными:

• 
  Стат ряд называют дискретным, если любые его варианты отличаются друг от друга на постоянную величину. В таких рядах задаются точечные значения признака.
  
• 
  Статистический ряд называется интервальным, если любые его варианты отличаются друг от друга на сколь угодно малую величину. Значения признака в них задаются в виде интервалов.
  

Если число значений признака Х велико, то варианты разбивают на отдельные интервалы, т.е. проводят их группировку.

На практике обычно считают, что правильно составленный ряд распределения содержит от 5 до 15 частичных интервалов.

Рекомендуемое число интервалов вычисляется по формуле Стерджеса:

m=1+3,322*lg(n)

Ширина (величина) интервала h равна:

5. 
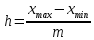
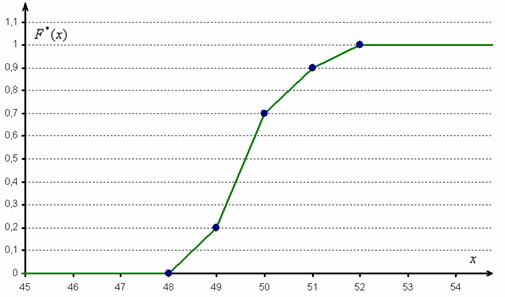
   Эмпирическая функция распределения, её график и свойства.
   

Эмпирической (статистической) функцией распределения Fn(x) называется функция, равная относительной частоте того, что признак (СВ Х) примет значение меньшее заданного действительного числа х, т.е. функция, определяющая, для каждого значения х частость события {X


х-любое действительное число

Свойства эмпирической функции распределения:

• 
  Значение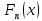 принадлежат отрезку [0;1]
  
• 
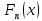  является неубывающей функцией
  
• 
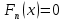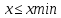
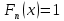  при
  
• 
  при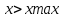
  

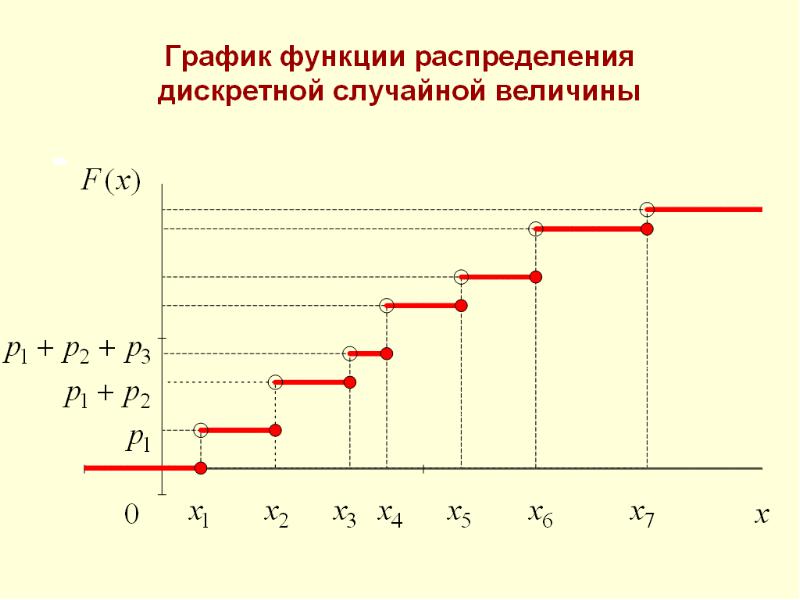
Для дискретного статистического ряда:

хi	x1	x2	…	xk
ωi	ω1	ω2	…	ωk

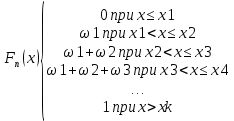
Для интервального статистического ряда:

---

xi	(x1;x2]	(x2;x3]	…	(xk-1;xk]
ωi	ω1	ω2	…	ωk

• 
  F(x)=0 при x≤x1
  
• 
  F(x2)= ω1
  
• 
  F(x3)= ω1+ ω2
  
• 
  F(x4)= ω1+ ω2+ ω3
  
• 
  …
  
• 
  F(xk)= ω1+ ω2+ …+ ωk-1+ ωk=1
  
• 
  F(x)=1 при x>xk
  

6. 
   Графическое представление статистических рядов: полигон и гистограмма.
   

Полигон как правило служит для изображения дискретного статистического ряда. Полигон частот (или частостей) – это ломаная, отрезки которой соединяют точки с координатами (xi;ni) или (xi;ωi), i=1,2,…k.

Варианты (xi) откладывают на оси абсцисс, а частоты или частости – на оси ординат.



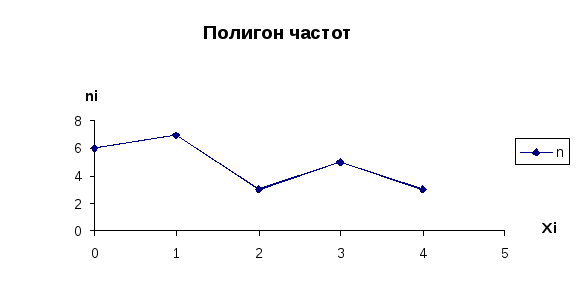
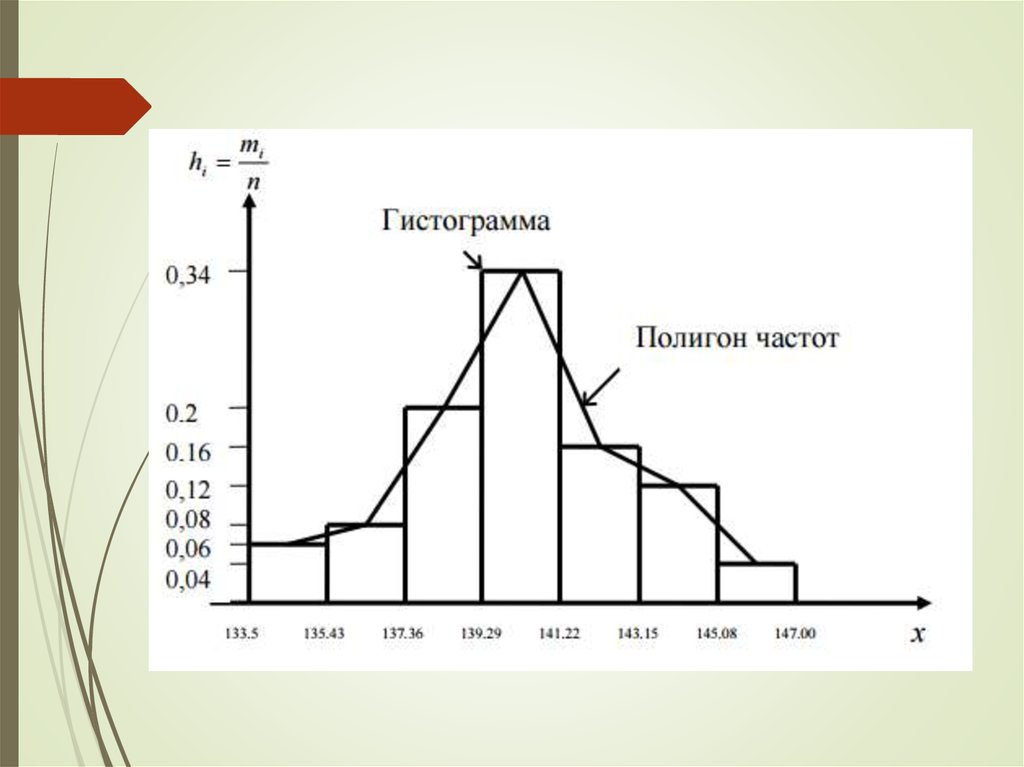
Гистограмма (т.е. столбчатая диаграмма) служит только для изображения интервальных статистических рядов. Гистограмма частот или частостей – это ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы (xi; xi+1), i=1,2,…m, а высоты равны частотам (ni) или частостям (ωi).

7. 
   Выбросы. Диаграмма размаха (ящик с усами).
   

8. 
   Числовые характеристики выборочных распределений: выборочная средняя, мода, медиана, показатели вариации, показатели формы.
   

Числовые характеристики признака Х, рассчитанные по выборке, называются выборочными характеристиками этого признака. Выборочные характеристики являются случайными величинами, а не константами.

Пусть дано стат распределение выборки объема n

А) Дискретный статистический ряд частот:

Значение признака xi	x1	x2	…	xk
Частота ni	n1	n2	…	nk

Б) Интервальный статистический ряд частот

(xi-1;xi)	(x1;x2]	(x2;x3]	…	(xk-1;xk]
ni	n1	n2	…	nk

---

I Характеристика центра распределения (средние)

• 
  Выборочная средняя – это среднее арифметическое всех значений выборки:
  
  • 
    Простая – используется, когда данные наблюдения не сведены в вариационный ряд, либо когда все частоты равны 1 или одинаковы
    

• 
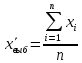
  Взвешенная – используется, когда частоты отличны друг от друга:
  

• 
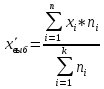
  Мода Мо вариационного (статистического) ряда – это вариант, которому соответствует наибольшая частота.
  
  • 
    Для дискретного вариационного ряда мода равна значению варианты с наибольшей частотой
    
  • 
    Мода интервального ряда определяется по формуле:
    

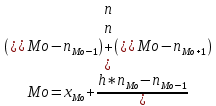
Где 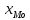- нижняя граница модального интервала

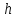-ширина интервала

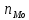- частота модального интервала

Модальным считается интервал, которому соответствует наибольшая частота

• 
  Медианой Ме вариационного (статистического) ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдений.
  
  • 
    Для дискретного вариационного ряда с нечетным числом членов медиана равна серединному варианту, а для ряда с четным числом членов, полусумме двух серединных вариантов, т.е.
    

Если n=2k+1, то медиана Ме=xk+1

Если n=2k, то медиана Me=(xk+xk+1)/2

• 
  Для интервального ряда медиана определяется по формуле:
  

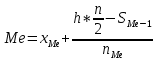
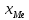-нижняя граница медианного интервала

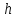-ширина интервала

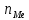- частота медианного интервала

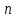-объем выборки

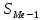- сумма частот (накопленная частота) до медианного интервала

Медианным считается интервал, которому принадлежит значение признака с номером n/2 (если n – четное) или (n+1)/2 (если n-нечетное)

---

II Показатели вариации признака

• 
  Выборочная дисперсия Dвыб – это среднее арифметическое квадратов отклонений значений признака от выборочной средней:
  
  • 
    Простая: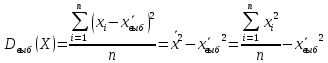
    
  • 
    Взвешенная: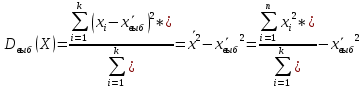
    
• 
  Выборочное среднее квадратическое отклонение (стандартное отклонение) – это арифметическое значение корня квадратного из выборочной дисперсии – рассчитывается по формуле: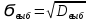
  
• 
  Размах вариации R – это число, равное разности между наибольшим и наименьшим вариантами ряда, т.е.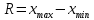
  
• 
  Выборочный коэффициент вариации равен процентному отношению выборочного СКО к выборочной средней, т.е.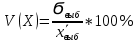
  
• 
  Выборочный начальный момент порядка k:
  

• 
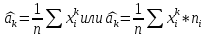
  Выборочный центральный момент порядка k:
  

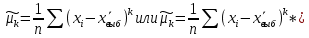
Ш показатели формы распределения признака:

• 
  Квантили (ранговые характеристики): q-квартили; d- децили; p-перцентили или процентили. – это значения признака, которые делят ранжированный ряд соответственно на 4, 10, 100 равных частей
  
• 
  Асимметрия А. Показывает различия в вариации значений признака по одну и другую сторону от средней.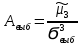
  
• 
  Эксцесс Е. Это показатель островершинности или плосковеришнности симметричного распределения по сравнению с нормальным распределением.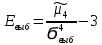
  
• 
  Асимметрия и эксцесс определяются для интервальных статистических рядов.
  

9. 
   Понятие статистической оценки параметров распределения. Виды стат. оценок.
   

Статистическое оценивание – это определение приближенного значения неизвестного параметра генеральной совокупности по результатам наблюдения.

Параметр θ – это числовая характеристика генеральной совокупности.

Статистической оценкой ( 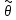) параметра тета называется его приближенное значение, зависящее от данных выбора.

Виды статистических оценок:

• 
  Точечные
  

---

Смотрите также файлы

• Возможно ли привлечение Сапожникова к административной ответственности.doc

• Мдк. 01. 01 Право социального обеспечения.docx

• Музыка в сопи.docx

• 1 Конвективный способ.docx

• Лабораторная работа 11 (5) определение момента инерции колеса и момента силы трения.docx