Файл: Практикум Составители Л. И. Шевелева, В. И. Максименко, А. Г. Голикова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.10.2023
Просмотров: 500
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Дальневосточный федеральный университет
1 ГИДРОГРАФ СТОКА И ЕГО ПОСТРОЕНИЕ
2 ХАРАКТЕРИСТИКИ СТОКА И ИХ ОПРЕДЕЛЕНИЕ
РАСЧЕТ ОРДИНАТ И ПОСТРОЕНИЕ ЭМПИРИЧЕСКОЙ И ТЕОРЕТИЧЕСКОЙ КРИВЫХ ОБЕСПЕЧЕННОСТИ РАСХОДОВ
Расчет координат теоретической кривой обеспеченности
ОПРЕДЕЛЕНИЕ КОРРЕЛЯЦИОННОЙ СВЯЗИ МЕЖДУ ГИДРОЛОГИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
182,718
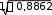 216,042
216,042 84,72 ;
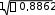 100,17 .
100,17 .Уравнения (21) и (22) с учетом погрешности х/y, y/xимеют вид:
у = 1,048х + 22,413 ± 100,17; х = 0,749у + 28,325 ± 84,72.
Чтобы построить линии, соответствующие уравнениям (21) и (22), надо задать два произвольных значения х и получить координаты у [для уравнения (21)] и, соответственно, задать два значения у, чтобы получить координаты х [для уравнения (22)], например, как показано в табл. 12. При больших значениях коэффициента корреляции угол между линиями регрессии маленький, и точность построения зависит от выбранного масштаба.
Таблица 12
Расчет координат уравнений регрессии
| Уравнение | y | x | x | y |
| x= 0,749y + 28,325 | 50 | 65,775 | | |
| | 800 | 627,525 | | |
| y= 1,048x + 22,413 | | | 50 | 74,813 |
| | | | 800 | 860,813 |
По этим координатам наносят линии регрессии на построенный ранее точечный график связи расходов двух рек (рис. 6). При правильном определении уравнений регрессии и их построении точка пересечения двух линий имеет координаты, соответствующие Х0 и Y0. Как видно на графике (рис. 7), уравнения (21) и (22) пересекаются в точке с координатами, соответствующими средним многолетним расходам: Х0 = 209,9 м3/с и
Y0 = 242,3 м3/с, значит, построение выполнено верно.
Практическое значение уравнений заключается в том, что по ним можно восстановить недостающие значения расходов за разные годы наблюдений.
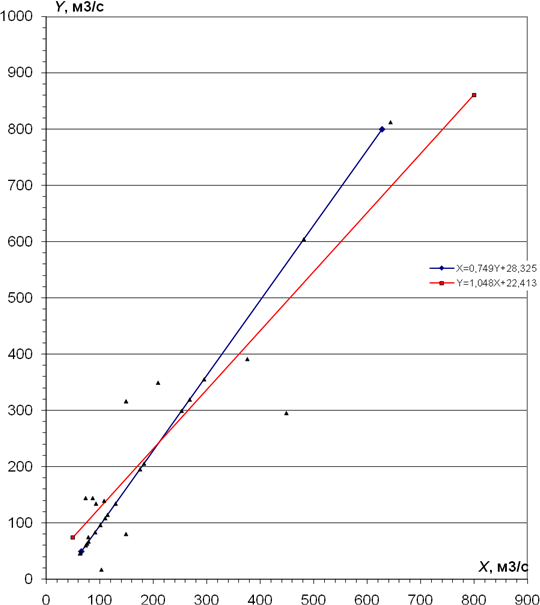
Рис. 7. График уравнений регрессии
Например, чтобы определить, какой среднегодовой расход был на исследуемой реке в 1951 г., надо в уравнение (22) подставить значение расхода на реке-аналоге в этот же год – 300 м3/с.
х= 0,749300 + 28,325 = 253 м3/с.
С учетом погрешности определения значений уравнения фактический расход может варьировать в диапазоне 253 ± 84,7 м3/с.
Аналогично рассчитывают все недостающие значения ряда, после чего находят средний многолетний расход (норма стока) на исследуемой реке.
Линии регрессии на графике пересекаются под некоторым углом . Величина этого угла свидетельствует о тесноте связи между двумя характеристиками (в данном случае – расходами). Чем меньше угол, тем выше коэффициент корреляции и теснее связь. Если коэффициент корреляции отрицательный, то имеет место обратная зависимость.
Задача 4.1
-
Определить наличие связи между двумя гидрологическими рядами. Рассчитать коэффициент корреляции и уравнения регрессии. Показать на графике связь между рядами хи у, нанести на график прямые, рассчитанные по уравнениям регрессии. -
Удлинить гидрологический ряд. Исходные данные приведены в табл. 13.
Таблица 13
Названия рек, между расходами которых надо проверить наличие корреляционной связи
| № варианта | Река 1 | Река 2 | ||
| Название | Число лет наблю- дений | Название | Число лет наблю- дений | |
| 1 | 81. Иман – с. Сидатун | 17 | 83. Иман – с. Картун | 44 |
| 2 | 81. Иман – с. Сидатун | 17 | 85. Иман – пос. Вагутон | 42 |
| 3 | 97. Эльдо-Вака – с. Мартынова поляна | 11 | 96. Сандо-Вака – с. Ясная Поляна | 36 |
| 4 | 95. Сандо-Вака – с. Вангоу | 11 | 96. Сандо-Вака – с. Ясная Поляна | 36 |
| 5 | 98. Тудо-Вака – с. Ариадное | 12 | 100. Тудо-Вака – с. Костюково | 37 |
| 6 | 164. Пфусунг – с. Щербаковка | 10 | 165. Пфусунг – с. Маргаритово | 31 |
| 7 | 184. Майхе – с. Ново-Хатуничи | 8 | 185. Майхе – с. Майхе | 41 |
| 8 | 202. Супутинка – Садовый (пос.) | 11 | 203. Супутинка – х. Син-Ден | 42 |
| 9 | 200. Супутинка – Комаровский (пос.) | 12 | 203. Супутинка – х. Син-Ден | 42 |
| 10 | 61. Лефу – с. Лефинка | 8 | 63. Лефу – с. Халкидон | 29 |
| 11 | 62. Лефу – с. Ивановка | 12 | 63. Лефу – с. Халкидон | 29 |
| 12 | 74. Золотая – с. Барано-Оренбургское | 9 | 73. Тахеяж – рзд. Таловый | 23 |
| 13 | 78. Синтухэ – с. Дворянка | 15 | 79.Синтухэ – с. Ильинка | 50 |
| 14 | 119. Подхоренок – Дормидонтовка (пос.) | 18 | 127. Хор – п. Хор | 40 |
| 15 | 129. Катэн – лпз Катэн | 9 | 127. Хор – п. Хор | 40 |
| 16 | 158. Тадуши – пос. Кавалерово (пос.) | 11 | 162. Аввакумовка – с. Ветка | 50 |
| 17 | 170. Сучан – с. Молчановка | 15 | 173. Сучан – г. Сучан | 31 |
| 18 | 181. Кангауз – с. Романовка | 11 | 182. Цимухе – пос. Шкотово | 28 |
| 19 | 204. Каменка – Каменский (пос.) | 12 | 203. Супутинка – х. Син-Ден | 42 |
| 20 | 205. Волха – Верхний (пос.) | 12 | 203. Супутинка – х. Син-Ден | 42 |
| 21 | 206. Волха – Нижний (пос.) | 12 | 203. Супутинка – х. Син-Ден | 42 |
| 22 | 207. Китайский Ключ – Китайский (пос.) | 12 | 212. Раковка – Опытный (пос.) | 43 |
Задача 4.2
Установить связь между средними годовыми модулями стока рек Амгунь (с. Гуга) и Горюн (с. Бактор) – левые притоки р. Амур (табл. 14).
Таблица 14
Средние годовые модули рек Амгунь и Горюн
| Год | Амгунь, х, л/с км2 | Горин, у, л/с км2 | Год | Амгунь, х, л/с км2 | Горин, у, л/с км2 |
| 1951 | 12,9 | 9,23 | 1963 | 9,20 | 5,30 |
| 1952 | 7,00 | 4,74 | 1964 | 12,6 | 9,34 |
| 1953 | 10,5 | 5,90 | 1965 | 11,4 | 8,80 |
| 1954 | 4,80 | 2,59 | 1966 | 8,54 | 6,23 |
| 1955 | 13,0 | 8,74 | 1967 | 9,61 | 6,94 |
| Год | Амгунь, х, л/с км2 | Горин, у, л/с км2 | Год | Амгунь, х, л/с км2 | Горин, у, л/с км2 |
| 1956 | 15,3 | 13,8 | 1968 | 7,20 | 5,26 |
| 1957 | 16,6 | 12,1 | 1969 | 12,5 | 10,1 |
| 1958 | 15,7 | – | 1970 | 12,8 | 9,56 |
| 1959 | 16,6 | 12,5 | 1971 | 12,5 | 11,1 |
| 1960 | 16,6 | 10,9 | 1972 | 18,4 | 13,8 |
| 1961 | 8,9 | – | 1973 | 12,0 | 7,05 |
| 1962 | 11,1 | 8,25 | 1974 | 9,60 | 5,52 |
| | | | 1975 | 12,8 | 7,76 |
Задача 4.3
Установить связь между средними годовыми модулями подземного (х) и поверхностного (у) стока (табл. 15).
Таблица 15
Средние годовые модули поверхностного и подземного стоков
| Год | Подземный сток, х, л/с км2 | Поверхностный сток, у, л/с км2 | Год | Подземный сток, х, л/с км2 | Поверхностный сток, у, л/с км2 |
| 1922 | 1,3 | 3,8 | 1934 | 2,6 | 5,7 |
| 1923 | 1,5 | 4,1 | 1935 | 2,6 | 6,0 |
| 1924 | 1,6 | 3,3 | 1936 | 3,1 | 5,7 |
| 1925 | 1,7 | 4,1 | 1937 | 3,3 | 5,9 |
| 1926 | 2,0 | 4,3 | 1938 | 3,1 | 6,7 |
| 1927 | 2,1 | 4,2 | 1939 | 2,7 | 6,7 |
| 1928 | 2,4 | 4,5 | 1940 | 2,8 | 7,7 |
| 1929 | 2,3 | 5,2 | 1944 | – | 5,4 |
| 1930 | 2,4 | 5,2 | 1945 | – | 4,9 |
| 1931 | 1,7 | 5,4 | 1946 | 3,4 | 7,7 |
| 1932 | 1,4 | 5,5 | 1947 | 3,5 | 7,9 |
| 1933 | 1,6 | 5,7 | 1948 | 3,7 | 8,1 |
-
ХАРАКТЕРИСТИКИ ВОДОХРАНИЛИЩА
При проектировании водохранилища и его эксплуатации используют зависимости площади водной поверхности от уровня воды в нем = f(Н)и объема воды в водохранилище Voт уровня V= f(Н).
Графики, показывающие зависимости площади водоема и его объема от глубины или высотных отметок, соответствующих различным уровням наполнения водоема, называют батиграфическими кривыми. Одна из них – кривая площадей, другая – кривая объемов.
Батиграфические характеристики можно построить для любого створа реки. Их вид зависит только от топографии местности. Расход реки, как и проектируемое водохранилище, не влияет на батиграфические характеристики. Исходными данными для их построения являются только крупномасштабные топографические карты.
Характеристики водохранилища используются на стадии его проектирования для определения характерных уровней воды в водохранилище: нормального подпорного уровня (НПУ) и уровня мертвого объема (УМО). По кривой площадей определяют зону максимального затопления после создания водохранилища, а также объем испарения при расчете потерь на испарение. В процессе эксплуатации по этим характеристикам отслеживают объем водохранилища. Он может быть определен в любой момент времени по измеренному на водомерном посту водохранилища уровню Н. Знание объема необходимо для оценки запасов воды, особенно в маловодные годы и в зимний период.
Чтобы установить зависимость