Файл: Курсовая работа по статике по дисциплине Теоретическая механика.doc
Добавлен: 29.10.2023
Просмотров: 131
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1 РАСЧЕТ ПЛОСКОЙ ШАРНИРНОЙ ФЕРМЫ
2 Расчет усилий в стержнях фермы
2.1 Определение усилий в стержнях фермы аналитическим методом вырезания узлов
2.2 Определение усилий в стержнях фермы графическим методом вырезания узлов
2.3 Определение усилий в стержнях фермы построением диаграммы Максвелла – Кремоны
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Тульский государственный университет»
Курсовая работа по статике
по дисциплине: «Теоретическая механика»
Схема 1 вариант 5
Разработала: студентка гр. ИБ360821
Волкова Евгения Александровна
Номер договора: ИИ00691-20, год поступления 2020
Руководитель: к.т.н., доц. Ткач О.А.
Тула, 2023
Содержание
1 РАСЧЕТ ПЛОСКОЙ ШАРНИРНОЙ ФЕРМЫ 3
1.1Определение опорных реакций аналитическим способом 4
2 Расчет усилий в стержнях фермы 6
2.1 Определение усилий в стержнях фермы аналитическим методом вырезания узлов 6
2.2 Определение усилий в стержнях фермы графическим методом вырезания узлов 12
2.3 Определение усилий в стержнях фермы построением диаграммы Максвелла – Кремоны 14
2.4 Определение усилий в стержнях фермы методом Риттера 16
3. РАСЧЕТ ПЛОСКИХ СОСТАВНЫХ КОНСТРУКЦИЙ 21
3.1. Расчет конструкции № 1 21
3.2. Расчет конструкции № 2 23
3.3. Расчет конструкции № 3 25
3.4. Расчет конструкции № 4 29
4. РАСЧЕТ ПРОСТРАНСТВЕННОЙ КОНСТРУКЦИИ 32
ВЫВОДЫ 34
СПИСОК ЛИТЕРАТУРЫ 35
1 РАСЧЕТ ПЛОСКОЙ ШАРНИРНОЙ ФЕРМЫ
Исследуется равновесие твердых тел и их систем на примере таких технически важных конструкций, как плоские шарнирные фермы, балки, валы, плиты и пластинки с использованием аналитических и графических методов. Для каждой расчетной схемы составлены уравнения равновесия и определены реакции внешних и внутренних связей разными методами.
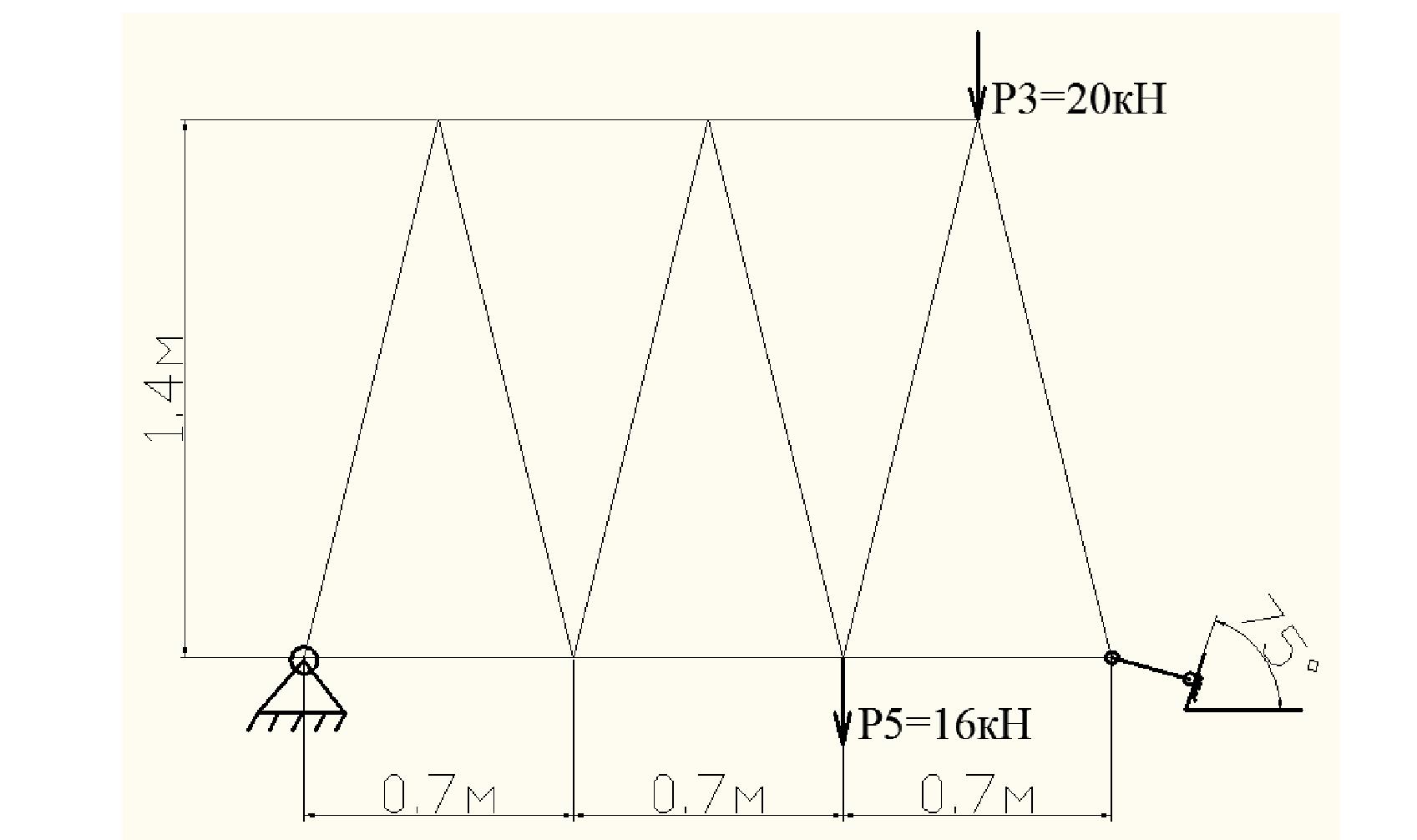
-
Определение опорных реакций аналитическим способом
Освободим ферму от опор, заменив их действие силами реакций связей
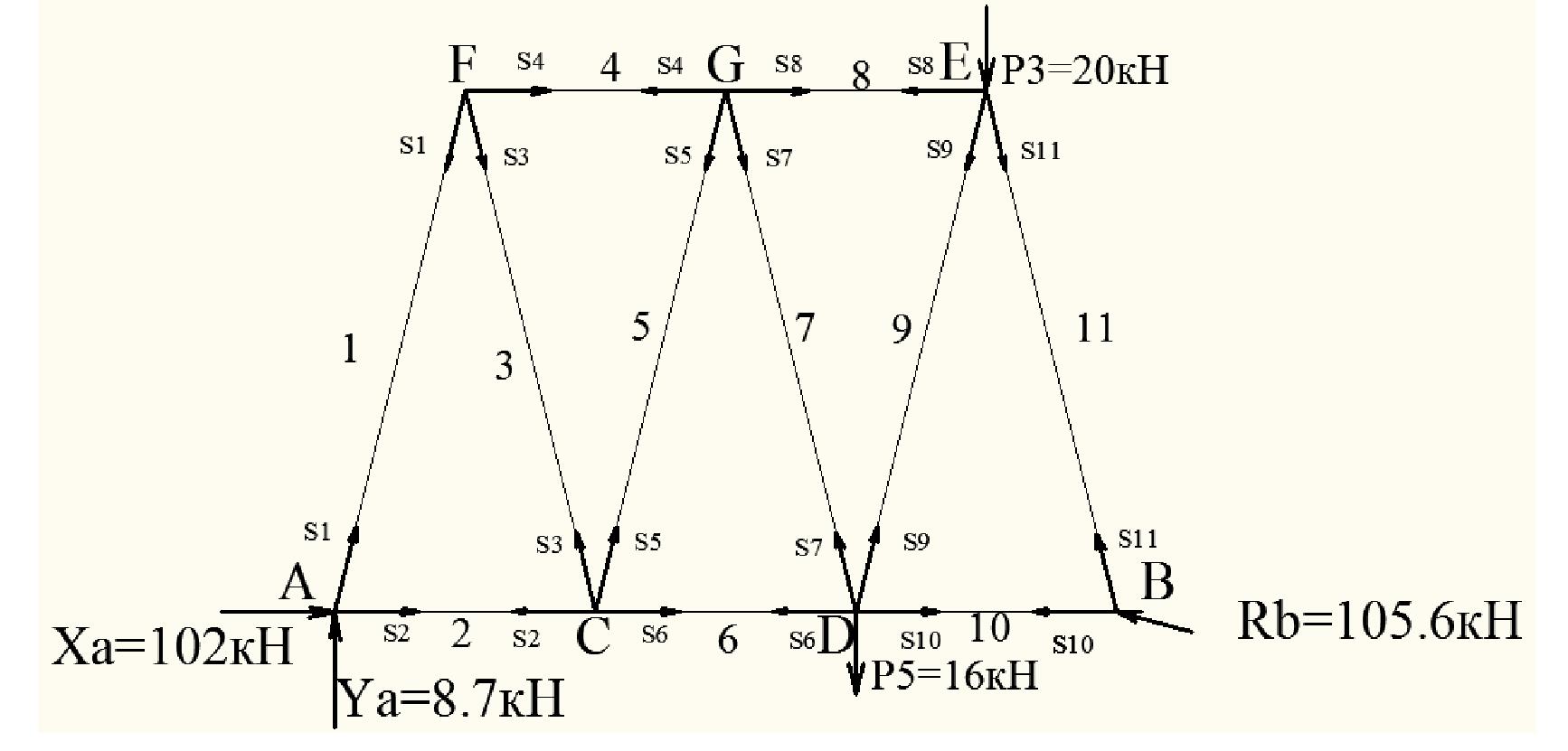
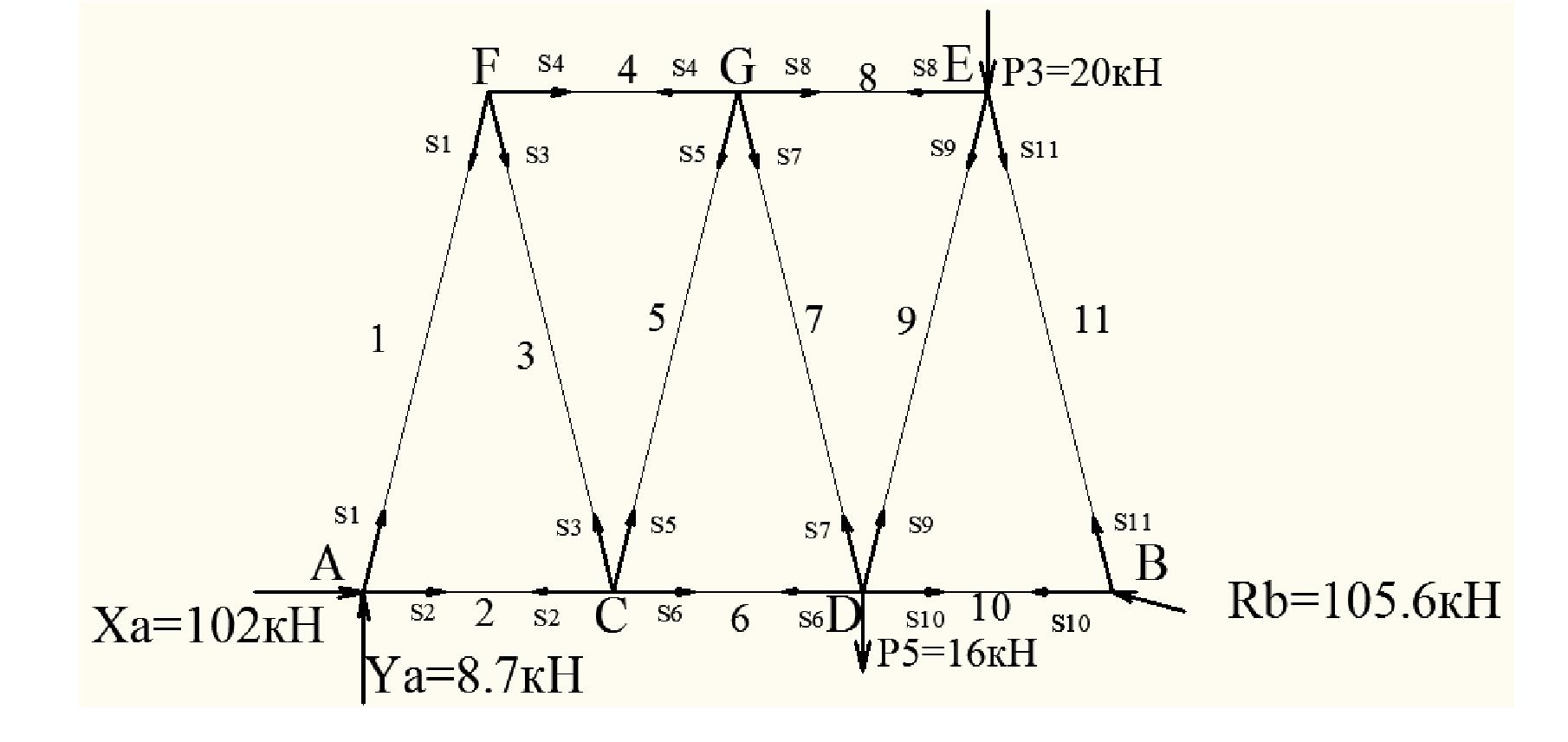
Расчетная схема изображена на рис. 2. На ферму действуют активные силы
А неизвестна ни по модулю, ни по направлению, поэтому ее разложим на две взаимно перпендикулярные составляющие силы Yа, Xа направив их как указано на расчетной схеме. Подвижная шарнирная опора В препятствует перемещению в направлении, перпендикулярном опорной плоскости, поэтому ее реакцию Rв направим также перпендикулярно опорной плоскости в вертикальном направлении. Таким образом, ферма находится в равновесии под действием произвольной плоской системы сил. Выбрав систему координат, составим уравнения равновесия сил, приложенных к ферме:
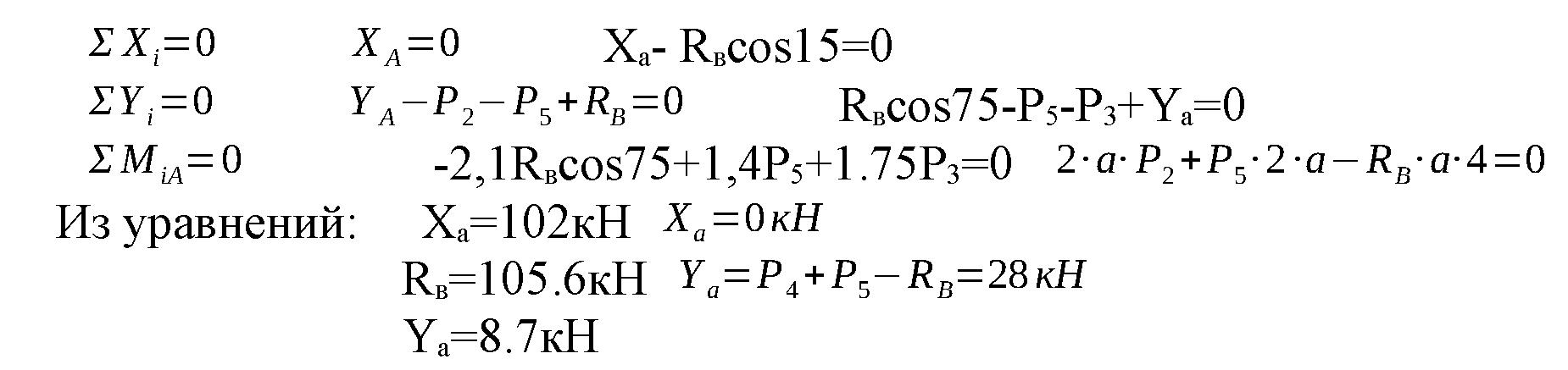
Все направления сил были выбраны правильно
2 Расчет усилий в стержнях фермы
2.1 Определение усилий в стержнях фермы аналитическим методом вырезания узлов
Для определения усилий в стержнях 1-13 вырежем узлы и рассмотрим равновесие сил, приложенных к каждому из них.
Узел А
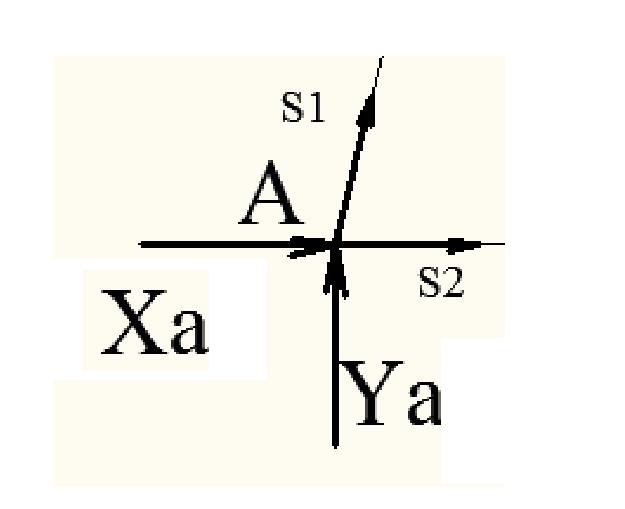
Система уравнений равновесия имеет вид:
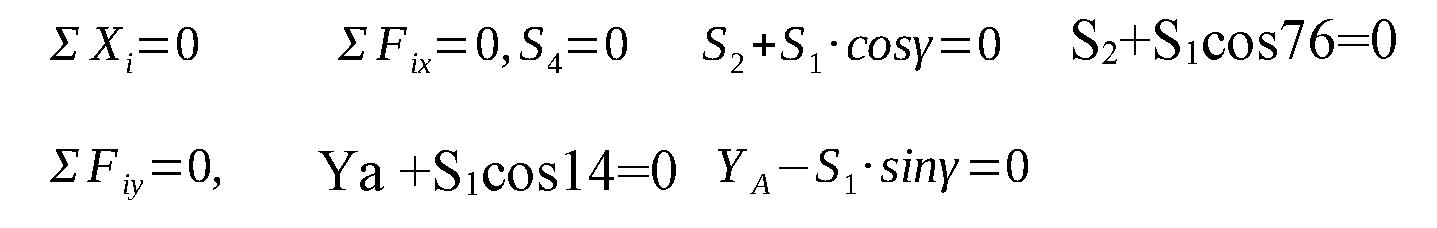
Узел B
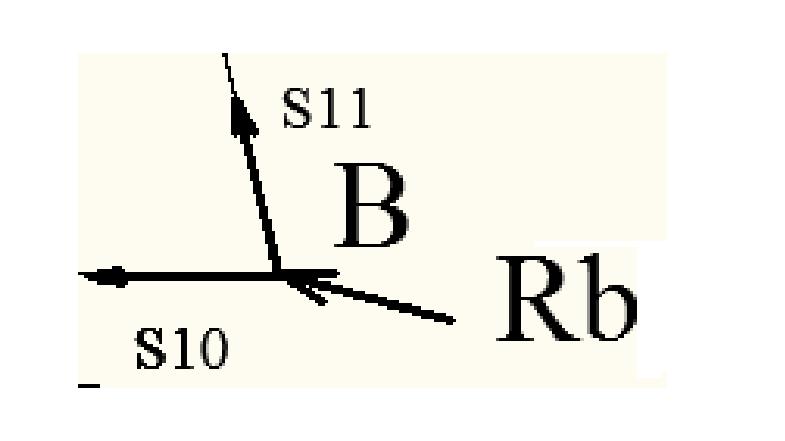
Система уравнений равновесия имеет вид:
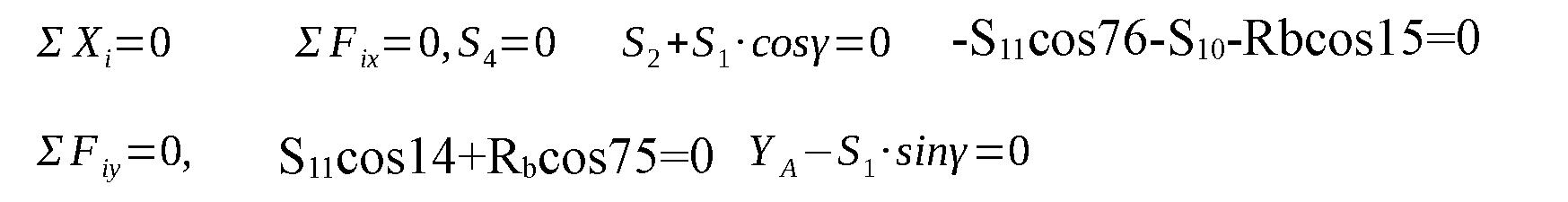
Из уравнений получаем:
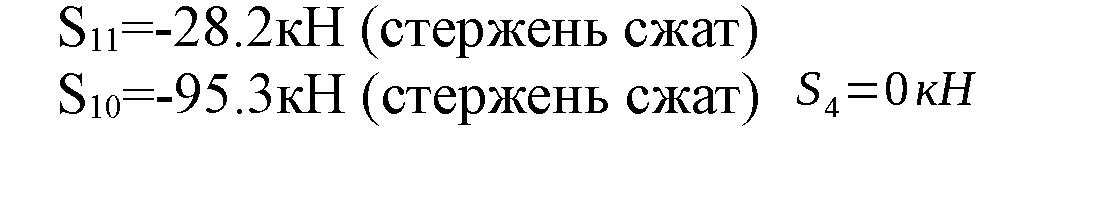
Узел E
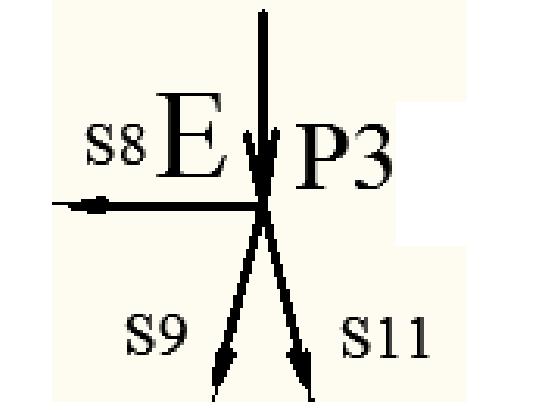
Система уравнений равновесия имеет вид:
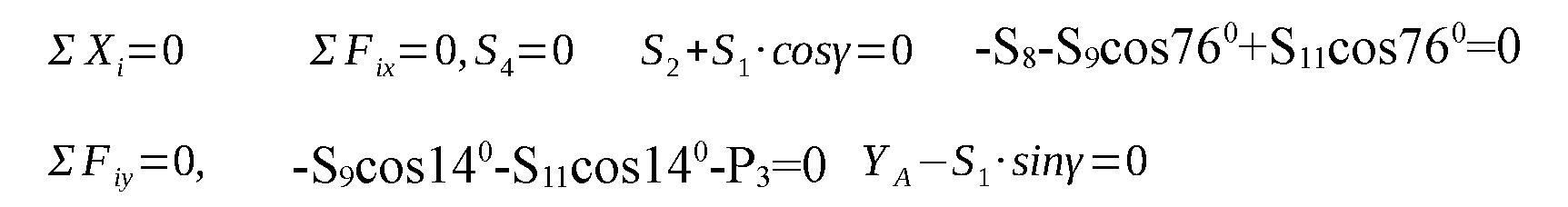
Из уравнений получаем:
Узел D
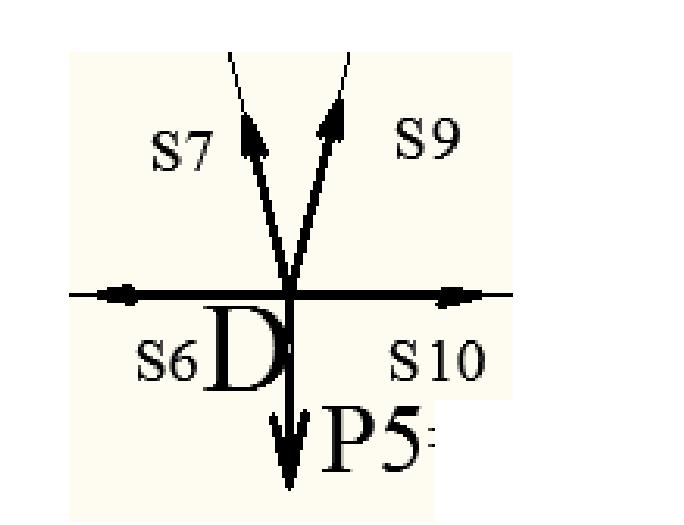
Система уравнений равновесия имеет вид:
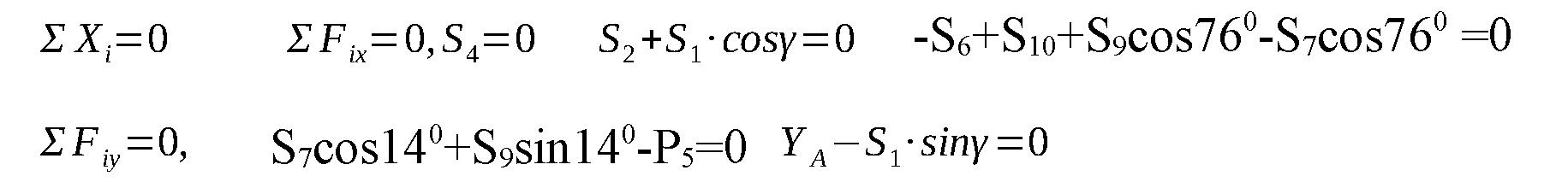
Из уравнений получаем:
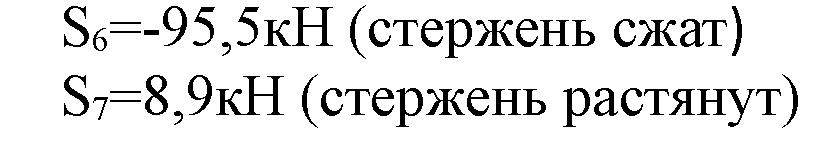
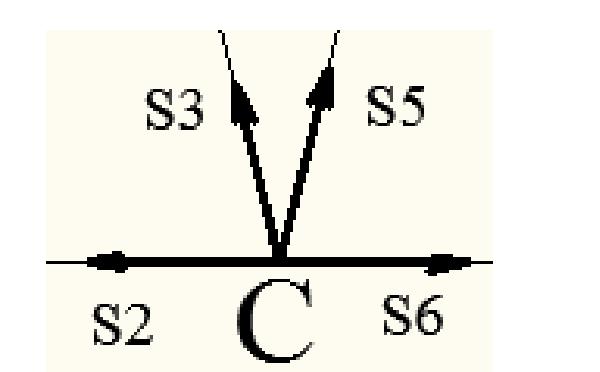
Узел C
Система уравнений равновесия имеет вид:
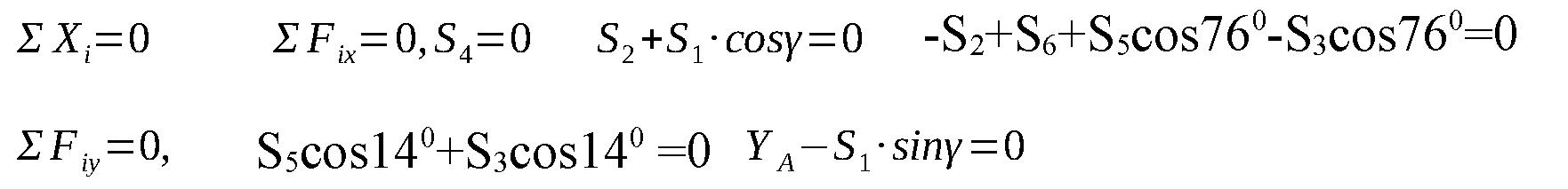
Из уравнений получаем:
Узел F
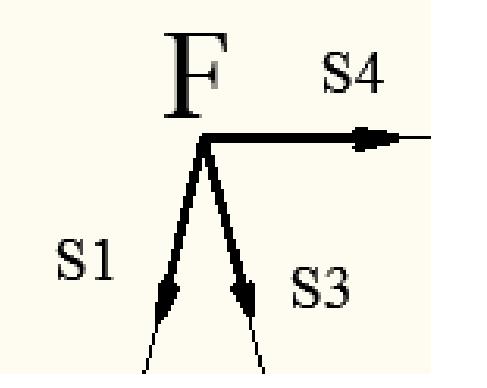
Из уравнения получаем:
Система уравнений равновесия имеет вид:
Из результатов расчетов следует, что реакции стержней 1,2,4,6,8,10,11 имеют направления, противоположные принятым на расчетной схеме. Следовательно, эти стержни сжаты. Результаты расчета поместим в таблицу.

2.2 Определение усилий в стержнях фермы графическим методом вырезания узлов
Известно, что для равновесия системы сходящих сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым. Это условие лежит в основе графического метода вырезания узлов. Рекомендуется следующая последовательность действий:
1) вычертить в масштабе ферму и изобразить (также в масштабе) все приложенные к ней заданные силы и ранее определенные реакции опор;
2) наметить последовательность узлов, которые необходимо вырезать для определения усилий в указанных стержнях (количество узлов для расчета определяет преподаватель);
3) вырезать узел, в котором сходятся два стержня, и рассмотреть его равновесие под действием заданных сил и реакций стержней; определить эти реакции построением в масштабе замкнутого многоугольника сил, приложенных к узлу;
-
рассмотреть, переходя от узла к узлу, равновесие остальных узлов в намеченной последовательности: при этом в узле должно быть только две неизвестные реакции стержней; построив для каждого узла замкнутый силовой многоугольник, определить все искомые усилия в стержнях; результаты построений внести в таблицу и сравнить их с аналитическим методом, предварительно определив характер работы стержней (сжатие или растяжение).
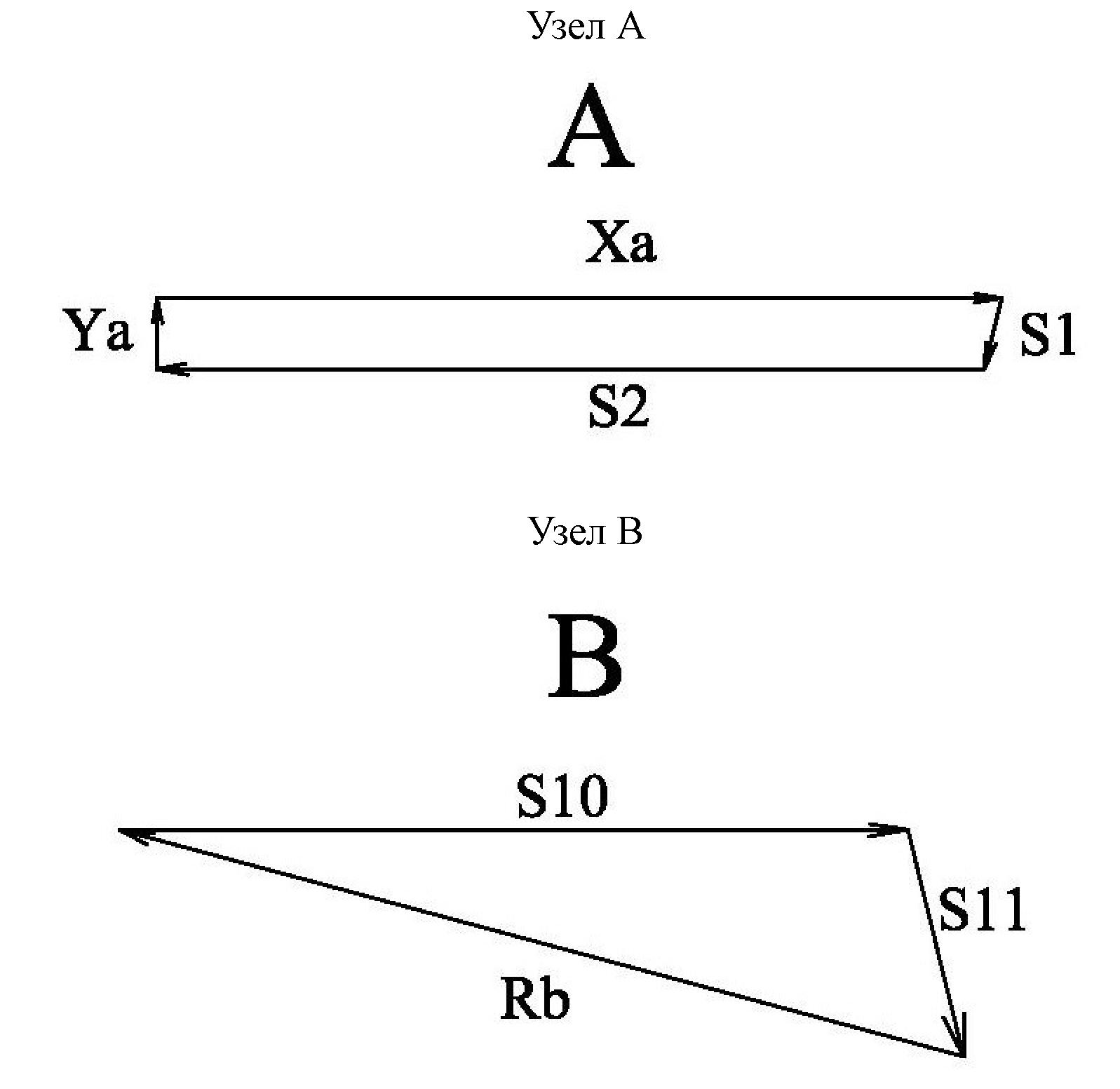

На рис изображена в масштабе ферма и показаны все активные силы и реакции опор. Для определения усилий в стержнях 1—11 необходимо вырезать узлы А, В, F, C, G, E. Масштаб (1см-1кН) A ,C, D, F, E
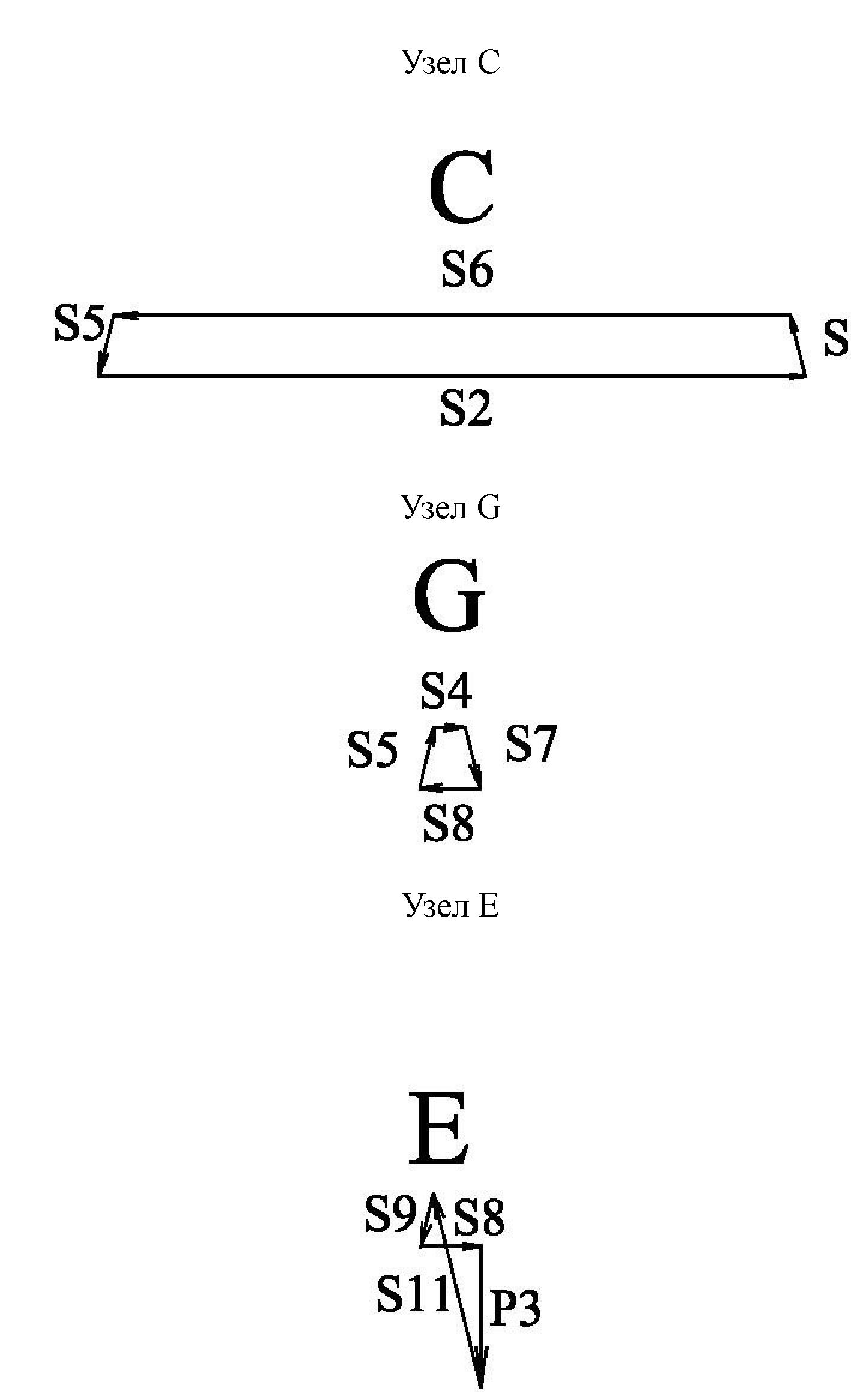

2.3 Определение усилий в стержнях фермы построением диаграммы Максвелла – Кремоны
-
Опорные реакции определены. -
Строим ферму в масштабе длин и изобразили все заданные силы и реакции опор в масштабе сил так, чтобы они были расположены вне контура фермы. -
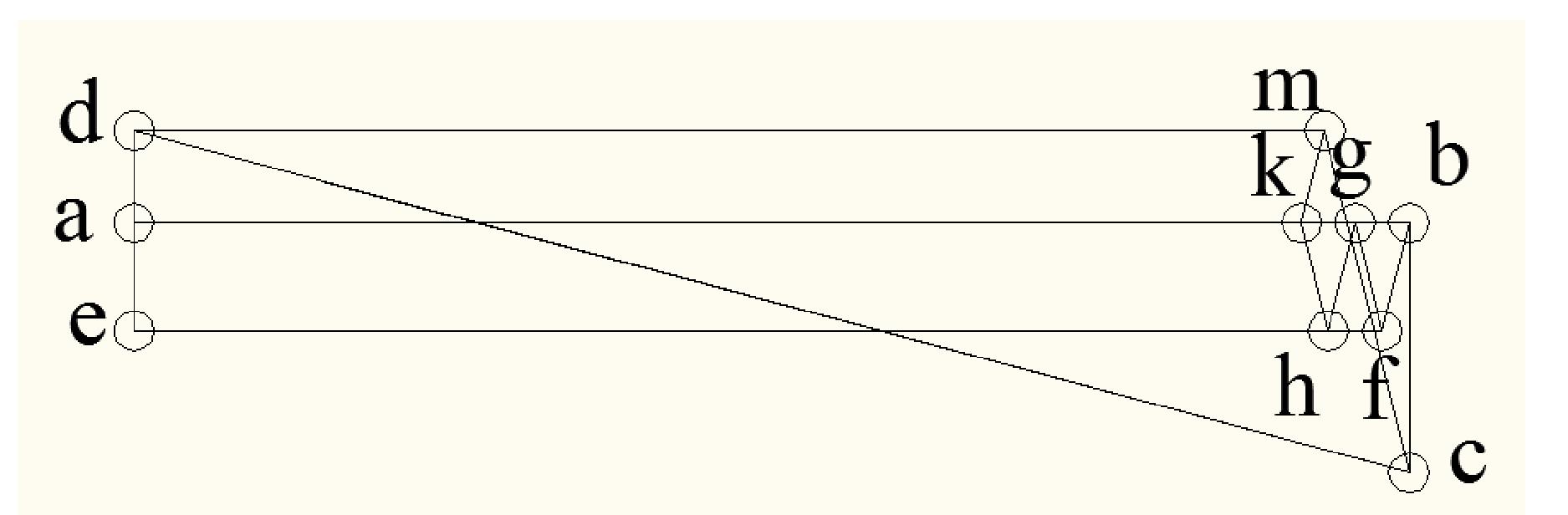
Выбрать направление обхода контура фермы и ее узлов по ходу часовой стрелки, и обозначили большими буквами латинского алфавита A ,B,C, D, E области, ограниченные внешними силами и стержнями фермы, а также внутренние области, ограниченные только стержнями: F, G, H, KE,F ,G, H ,J , I, M
-
Построили многоугольник внешних сил, отложив в нем силы в том порядке, в котором они встречаются при обходе фермы в выбранном направлении, и обозначив их малыми буквами, соответствующими названиям пограничных областей. Многоугольник внешних сил abcde. -
Используя графический метод вырезания узлов, к многоугольнику внешних сил последовательно пристраиваем силовые многоугольники для всех узлов фермы, начиная с узла, где сходятся два стержня, обозначив реакции стержней по тому же правилу, что и внешние силы. Выполнив такое построение для остальных узлов фермы, получили диаграмму Максвелла – Кремоны. -
Определили с учетом масштаба численное значение всех усилий в стержнях, и характер работы их, и результаты занесли в таблицу.
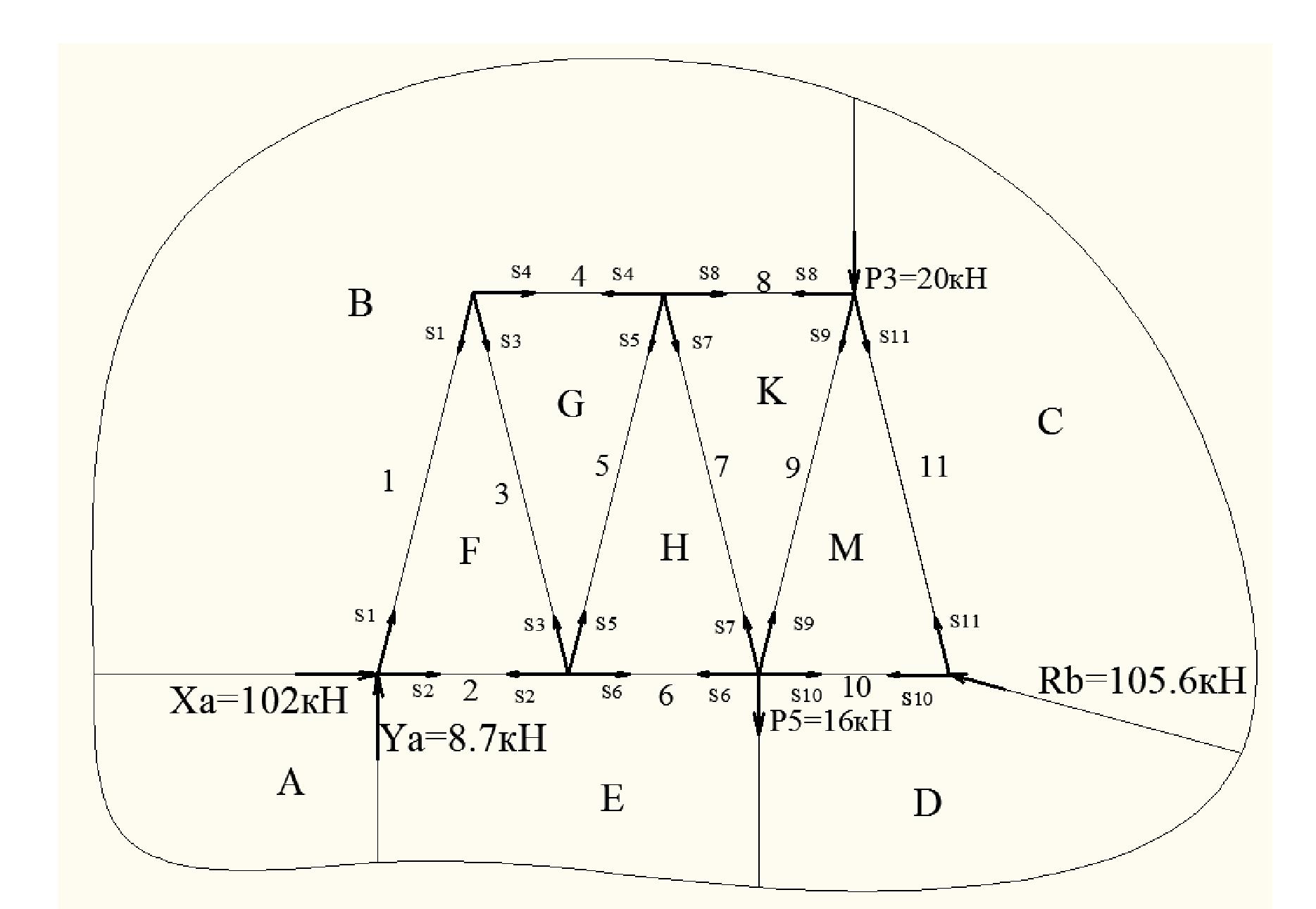

2.4 Определение усилий в стержнях фермы методом Риттера
Метод Риттера (способ сечений) в общем случае предполагает предварительное определение реакций опор фермы. Если реакции опор фермы определены, то метод Риттера позволяет найти усилие в данном стержне, при этом, как правило, определение усилия является автономным, т.е. не связанным с определением усилий в других стержнях.
1) Опорные реакции определены, разрезаем ферму на три части; сечение (1 – 1) по стержням 2,3,4; сечение (2 – 2) по стержням 4,5,6 сечение (3– 3) по стержням 6,7,8 сечение (4 – 4) по стержням 8,9,10
и рассматриваем в первом случае левую часть конструкции, во втором – левую, в третьем правую
2) Составляем для выбранной части фермы уравнения равновесия –
уравнения моментов относительно точек пересечения линий действия
неизвестных сил (точки Риттера). Если два стержня в сечении параллельны,
то для определения усилия в третьем стержне нужно составляем уравнение
проекций сил на ось, перпендикулярную к этим стержням;
3) Решаем каждое из составленных уравнений, определив искомые усилия.
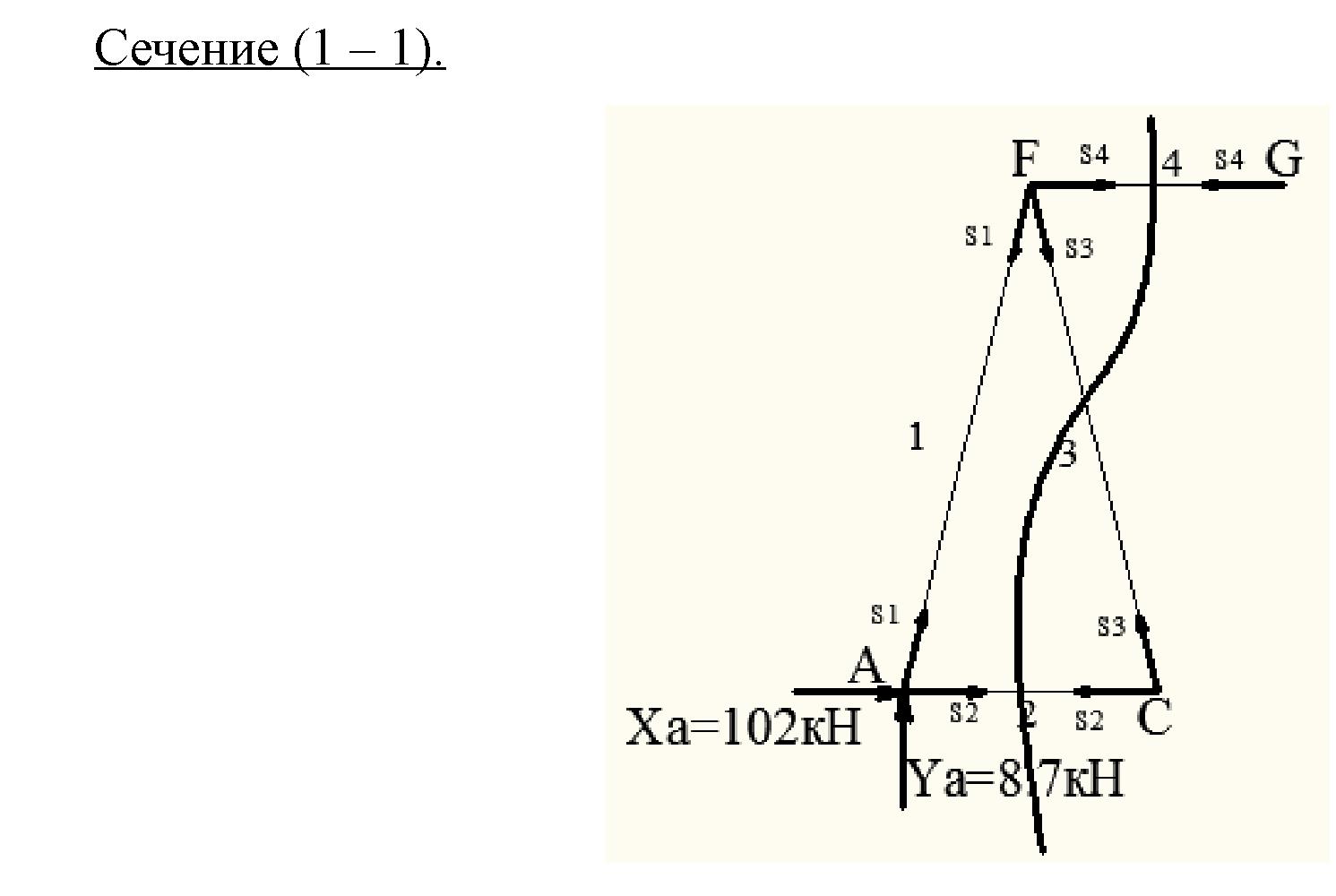
Чтобы определить усилие S4 независимо от усилий S3 S4,S6 , S2, составляем уравнение моментов сил относительно узла C, в котором пересекаются линии действия сил S3 S4,S6 , S2:
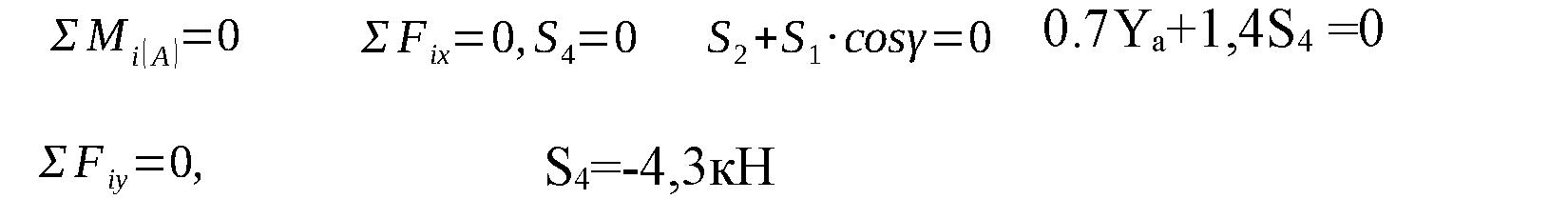
Чтобы определить усилие S2 независимо от усилий S3 S4,S6 , S4, составляем уравнение моментов сил относительно узла F A, в котором пересекаются линии действия сил S3 S4 ,S6 S4 ,S6 , S4:
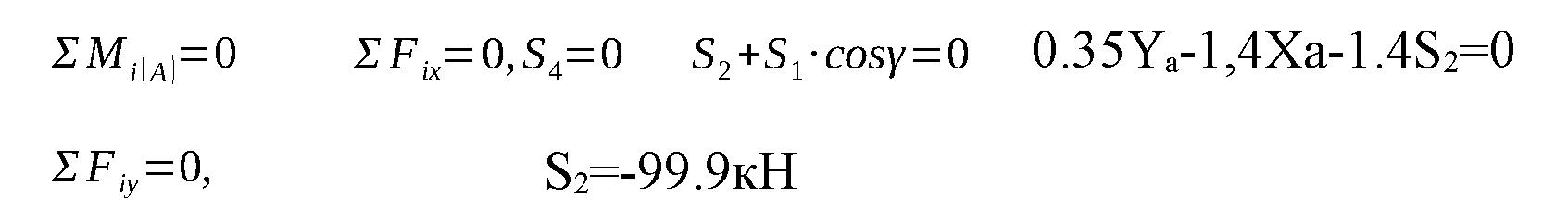
Чтобы определить усилие S3 составляем уравнение сил на ось y