Файл: Отчет по практической работе 7 реализация заданной логической функции от четырех переменных на дешифраторах 416, 38 и 24 по дисциплине.docx
Добавлен: 30.10.2023
Просмотров: 128
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 |
| МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ |
| Федеральное государственное бюджетное образовательное учреждение высшего образования "МИРЭА - Российский технологический университет" РТУ МИРЭА |
| Институт искусственного интеллекта |
| Кафедра общей информатики |

| ОТЧЕТ ПО ПРАКТИЧЕСКОЙ РАБОТЕ №7: реализация заданной логической функции от четырех переменных на дешифраторах 4-16, 3-8 и 2-4 | |
| по дисциплине | |
| «ИНФОРМАТИКА» | |
| Выполнил студент группы ИНБО-01-22 | |
| Принял старший преподаватель кафедры ОИ | Смирнов С.С. |
| Практическая | «»2022 г. |  |
| работа выполнена | | (подпись студента) |
| «Зачтено» | «»2022 г. |  |
(подпись преподавателя)
Москва 2022
СОДЕРЖАНИЕ
1 ПОСТАНОВКА ЗАДАЧИ 3
1.1 Постановка задачи 3
1.2 Персональный вариант 3
2 ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯ 4
2.1 Восстановление таблицы истинности 4
2.4 Реализация функции с помощью дешифраторов 2-4 7
3 ВЫВОДЫ 9
4 СПИСОК ИНФОРМАЦИОННЫХ ИСТОЧНИКОВ 10
1 ПОСТАНОВКА ЗАДАЧИ
1.1 Постановка задачи
Логическая функция от четырех переменных задана в 16-теричной векторной форме. Восстановить таблицу истинности. По таблице истинности реализовать в лабораторном комплексе логическую функцию на дешифраторах тремя способами:
-
используя дешифратор 4-16 и одну дополнительную схему «или»; -
используя два дешифратора 3-8 и необходимую дополнительную логику; -
используя пять дешифраторов 2-4 и одну дополнительную схему «или».
Протестировать работу схем и убедиться в правильности их работы. Подготовить отчет о проделанной работе и защитить ее.
1.2 Персональный вариант
Персональный вариант:
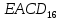 – 16-теричная векторная форма логической функции от четырех переменных
– 16-теричная векторная форма логической функции от четырех переменных2 ПРОЕКТИРОВАНИЕ И РЕАЛИЗАЦИЯ
F(a,b,c,d) =
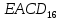
Преобразуем её в двоичную запись:
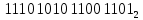
2.1 Восстановление таблицы истинности
На основании данных восстановим таблицу истинности (Таблица 1).
Таблица 1 – Таблица истинности
| a | b | c | d | F |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
2.2 Реализация функции с помощью дешифратора 4-16
Реализуем функцию, используя дешифратор 4-16 и одну дополнительную схему «или». Подадим значения переменных функции на адресные входы дешифратора: младшую переменную «d» - на младший адресный вход, старшую переменную «a» - на старший адресный вход, прочие переменные – аналогично. Объединим выходы дешифратора, номера которых совпадают с номерами значений переменных, на которых функция равна единице, через «или» и получим нужную реализацию (рис.1).
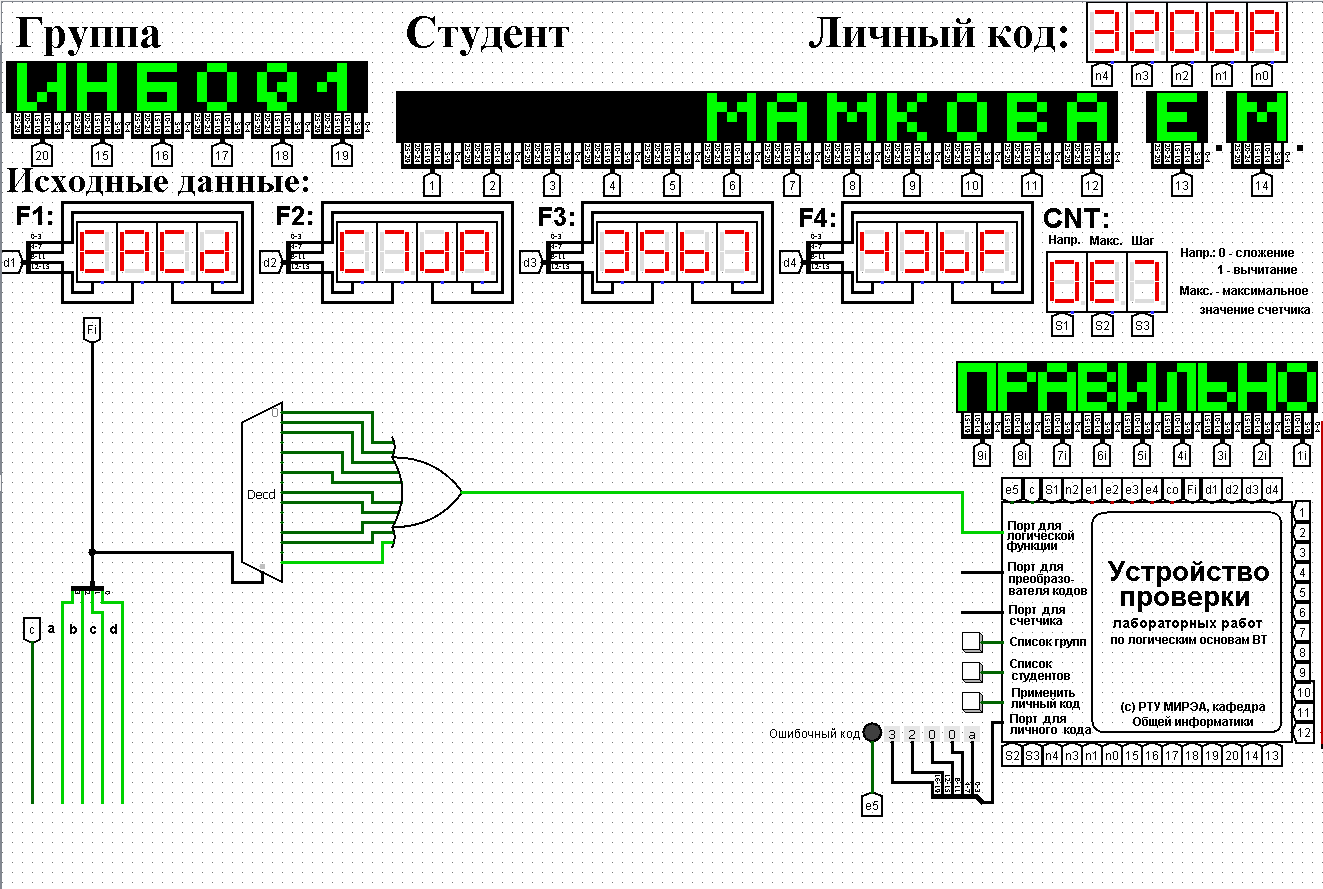
Рис.1 Тестирование схемы, реализующей логическую функцию на дешифраторе 4-16
Тестирование показало, что схема работает правильно.
2.3 Реализация функции с помощью дешифраторов 3-8
Реализуем функцию, используя два дешифратора 3-8 и дополнительную логику. Распределим области таблицы истинности между дешифраторами 3-8 (рис. 2). Подадим значения трех младших переменных функции на адресные входы обоих дешифраторов: младшую переменную «d» - на младший адресный вход, старшую переменную «b» - на старший адресный вход, а переменную «с» - на средний адресный вход.







Область ответствен-
ности второго дешифратора
Работа второго дешифратора
Работа первого дешифратора
| a | b | c | d | F |
 0 0 |  0 0 | 0 | 0 |  Область ответствен- ности первого дешифратора 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
 1 1 | 0 | 0 |  0 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Рис.2 Распределение областей таблицы истинности между дешифраторами 3-8
Построим в лабораторном комплексе комбинационные схемы. У первого дешифратора выберем лишь те выходы, чьи номера совпадают с номерами наборов значений переменных, на которых функция равна единице, из первой половины таблицы. У второго дешифратора выберем лишь те выходы, чьи номера совпадают с номерами наборов значений переменных, на которых функция равна единице, из второй половины таблицы. Объединим выходы дешифратора, номера которых совпадают с номерами значений переменных, на которых функция равна единице, через «или» и получим нужную реализацию (рис.3).
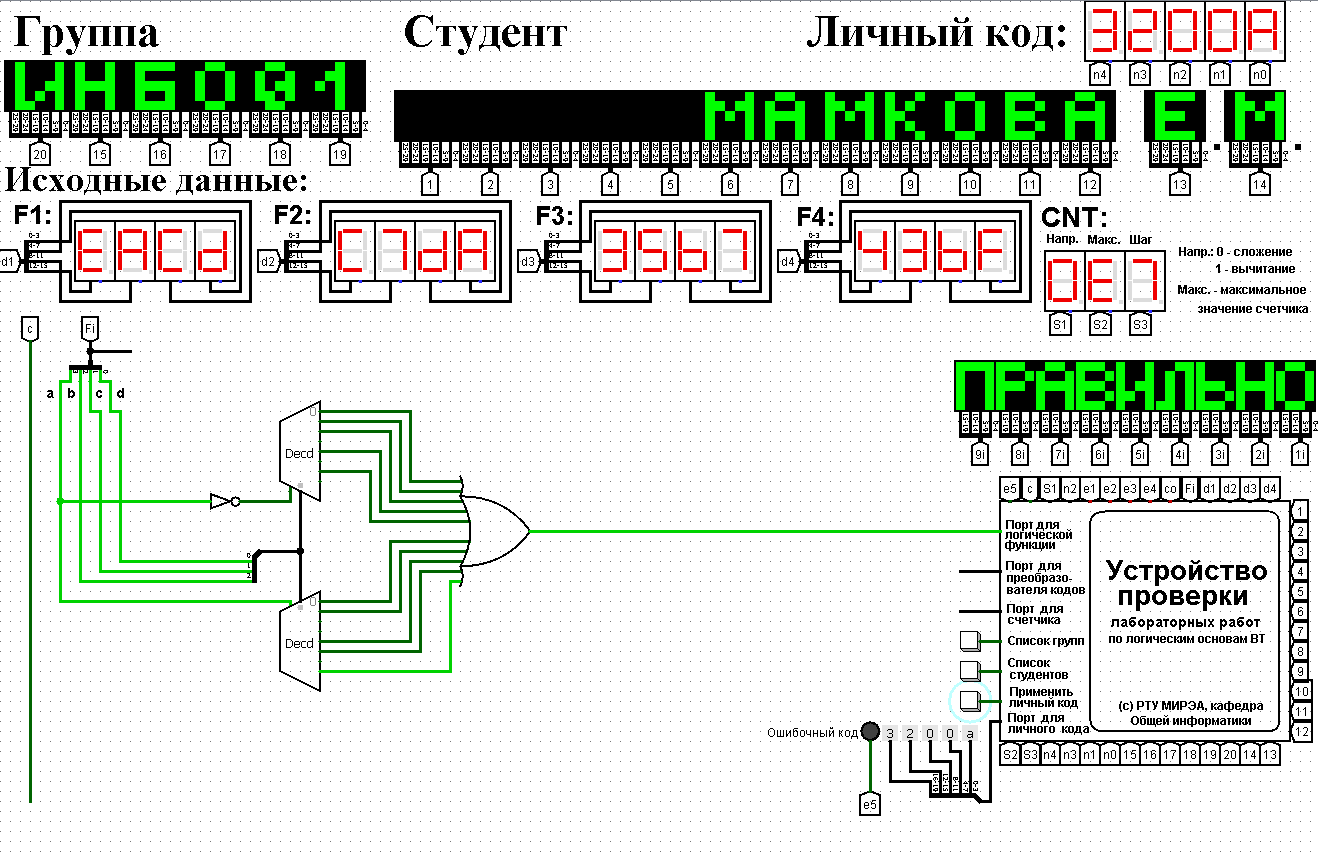
Рис.3 Тестирование схемы, реализующей логическую функцию на дешифраторах 3-8 и дополнительной логике
Тестирование показало, что схема работает правильно.
2.4 Реализация функции с помощью дешифраторов 2-4
Реализуем функцию, используя пять дешифраторов 2-4 и дополнительную логику. Распределим области таблицы истинности между дешифраторами 2-4 (рис. 4). Подадим значение переменной «d» на младший адресный вход, а значение переменной «с» на старший адресный вход. Переменные «а» и «b» используется для управления операционными дешифраторами, поэтому аналогичным образом подадим их на адресные входы управляющего дешифратора.













Область ответствен-
ности второго дешифратора
Работа второго дешифратора при комбинации 01
Работа второго дешифратора при комбинации 10
Работа второго дешифратора при комбинации 10
Работа первого дешифратора при комбинации 00 на адресных входах управляющего дешифратора
| a | b | c | d | F |
 0 0 |  0 0 | 0 | 0 |  Область ответствен- ности первого дешифратора 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
 0 0 | 1 | 0 |  0 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 |  0 0 | 0 |  0 0 |  Область ответствен- ности третьего дешифратора 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 |  1 1 | 0 | 0 |   Область ответствен- ности четвертого дешифратора 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |