Файл: Нормальные формы для формул алгебры высказываний 1 Правила построения скнф по таблице истинности 2.docx

Оглавление

Нормальные формы для формул алгебры высказываний

Понятие нормальных форм

• 
  Конъюнктивным одночленом от переменных X₁, X₂, ..., X_n называется конъюнкция этих переменных или их отрицаний. Здесь "или" употребляется в не исключающем смысле, т.е. в конъюнктивный одночлен может входить одновременно и переменная, и ее отрицание.
  
• 
  Дизъюнктивным одночленом от переменных X₁, X₂, ..., X_n называется дизъюнкция этих переменных или их отрицаний (и здесь союз "или" употребляется в не исключающем смысле).
  
• 
  Дизъюнктивной нормальной формой называется дизъюнкция конъюнктивных одночленов.
  
• 
  Аналогично конъюнктивной нормальной формой называется конъюнкция дизъюнктивных одночленов
  

Совершенные нормальные формы

Среди множества дизъюнктивных (равно как и конъюнктивных) нормальных форм, которыми обладает данная формула алгебры высказываний, существует уникальная форма: она единственна для данной формулы.

Это так называемая совершенная дизъюнктивная нормальная форма (среди конъюнктивных форм — совершенная конъюнктивная нормальная форма).

• 
  Совершенной конъюнктивной нормальной формой (СКНФ), относительно некоторого заданного конечного набора переменных, называется такая КНФ, у которой в каждую дизъюнкцию входят все переменные данного набора, причём в одном и том же порядке.
  
• 
  Совершенной дизъюнктивной нормальной формой (СДНФ), относительно некоторого заданного конечного набора переменных, называется такая ДНФ, у которой в каждую конъюнкцию входят все переменные данного набора. (либо сами, либо их отрицания).
  

---

Поскольку (С)КНФ и (С)ДНФ взаимодвойственны, свойства (С)КНФ повторяют все свойства (С)ДНФ, грубо говоря, «с точностью до наоборот».

Правила построения СКНФ по таблице истинности:

Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.

Правила построения СДНФ по таблице истинности:

Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0, берутся с отрицанием.

Множества, отношения, функции в логике

Определение бинарного отношения

Определение функции

Булева функция

• 
  Булевой функцией от одного аргумента называется функция f, заданная на множестве из двух элементов и принимающая значения в том же двухэлементном множестве.
  

Элементы двухэлементного множества будем обозначать 0 и 1. Таким образом, f: {0;1} → {0;1}. Нетрудно перечислить все булевы функции от одного аргумента:

• 
  Булевой функцией от двух аргументов называется функция g, заданная на множестве {0;1} х {0;1} и принимающая значения в двухэлементном множестве {0;1}. Другими словами, булева функция от двух аргументов сопоставляет любой упорядоченной паре, составленной из элементов 0 и 1 (а таких упорядоченных пар будет четыре), либо 0, либо 1.
  

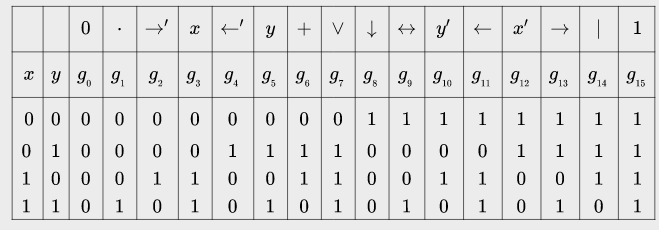
Перечислим все возможные булевы функции от двух аргументов в форме следующей таблицы:

• 
  Первые две функции, которые рассматриваются, g₀(x, y) = 0 и g₁₅(x, y) = 1 — тождественный ноль и тождественная единица.
  

• 
  Далее, функция g1(x, y) называется конъюнкцией и обозначается x· y (или xy). Конъюнкция принимает значение 1 в том и только в том случае, когда оба ее аргумента принимают значение 1.
  

---

• 
  Отрицание конъюнкции, функция g₁₄(x, y), называется штрихом Шеффера и обозначается x | y. Таким образом, g₁₄(x, y) = (x· y)'=x | y. Эта функция принимает значение 0 в том и только в том случае, когда функция g₁(x, y) принимает значение 1, т.е. в случае, когда оба ее аргумента принимают значение 1.
  

• 
  Функция g₇(x, y) называется дизъюнкцией и обозначается x ∨ y. Таким образом, g₇(x, y) = x ∨ y.
  

• 
  Функция g₈(x, y), являющаяся отрицанием функции g₇(x, y), носит название стрелка Пирса (или функция Вебба) и обозначается x ↓ y. Итак, g₈(x, y) = (x ∨ y)'=x ↓ y
  

• 
  Функция g₁₃(x, y) называется импликацией и обозначается x → y, т.е. g₁₃(x, y) = x → y. Аргумент x в этой функции называется посылкой импликации, а аргумент y — ее следствием.
  

• 
  Отрицанием импликации является функция g₂(x, y) = (x → y)'. Специального названия она не имеет.
  

• 
  Функция g₁₁(x, y) называется антиимпликацией или обратной импликацией, потому что представляет собой импликацию с посылкой y и следствием x. Таким образом, g₁₁(x, y) = y → x.
  

• 
  Её отрицанием является функция g₄(x, y) = (y → x)', не имеющая названия.
  

• 
  Функция g₉(x, y) называется эквивалентностью и обозначается x ↔ y, так что g₉(x, y) =x ↔ y. Она принимает значение 1 тогда и только тогда, когда оба ее аргумента принимают одинаковые значения.
  

• 
  Функция g₆(x, y), являющаяся отрицанием функции g₉(x, y), называется сложением по модулю два, или суммой Жегалкина, и обозначается x + y.
  

• 
  Наконец остаются еще две пары функций. В первую пару входят функции g₃(x, y) и g₁₂(x, y). Первая из них принимает всегда те же самые значения, что и ее первый аргумент, т.е. g₃(x, y) = x, а вторая функция является отрицанием первой: g₁₂(x, y) = x'.
  

• 
  Во вторую пару входят функции g₅(x, y) и g₁₀(x, y). Первая из них принимает всегда те же самые значения, что и ее второй аргумент, а вторая функция является отрицанием первой: g₁₀(x, y) = y'.
  

Теперь установим некоторые важнейшие свойства введенных функций:

• 
  Две булевы функции f(x, y) и g(x, y) называются равными, если каждому набору значений аргументов x, y обе функции сопоставляют один и тот же элемент из множества {0;1}, т.е. f(a, b)=g(a, b) для любых a, b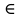 {0;1}. Например, x ∨ y=y ∨ x.
  
• 
  Из введенных простейших булевых функций можно строить с помощью суперпозиций более сложные булевы функции.
  

---

Например, если в функцию x ∨ t вставить вместо аргумента t функцию y· z, то получим следующую сложную функцию: x ∨ (y· z). Если в нее в свою очередь вставить вместо аргумента z функцию u → v, то получим сложную функцию x ∨ (y · (u → v)). И так далее. В результате получаются булевы функции от трех, четырех и большего числа аргументов.

• 
  Булевой функцией от n аргументов называется функция f, заданная на множестве {0;1}ⁿ и принимающая значения в двухэлементном множестве {0;1}. Другими словами, булева функция от n аргументов сопоставляет каждому упорядоченному набору длины n, составленному из элементов 0 и 1, либо 0, либо 1.
  

• 
  Две булевы функции от n аргументов f(x₁, x₂, ..., x_n) и g(x₁,x₂, ..., x_n) называются равными, если любым одинаковым наборам значений аргументов x₁,x₂, ..., x_n обе эти функции сопоставляют одинаковые элементы из множества {0;1}, т.е. f(а₁,а₂, ..., а_n)=g(а₁,а₂, ..., а_n) для
  
• 
  любых элементов а₁,а₂, ..., а_n ∈ {0;1}.
  

Выражение одних булевых функций через другие

Справедливы следующие равенства, выражающие одни булевы функции через другие:

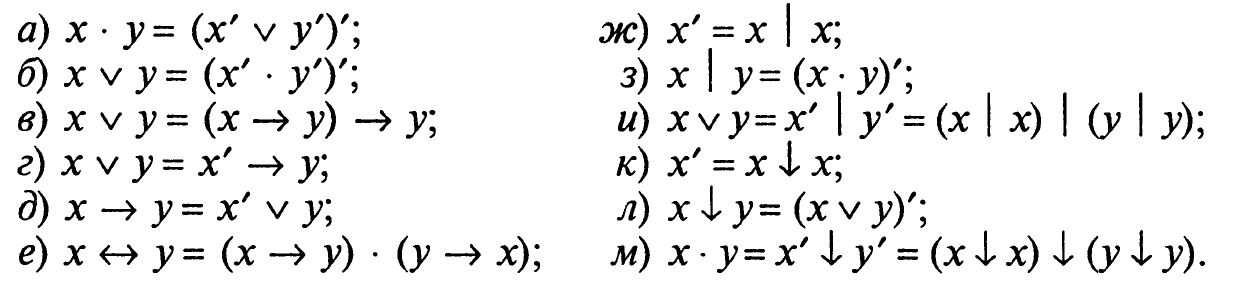
Суперпозиция булевых функций

Теорема о числе булевых функций от n аргументов:

• 
  Число различных булевых функций от n аргументов равно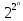
  

Лемма о разложении функции по переменной

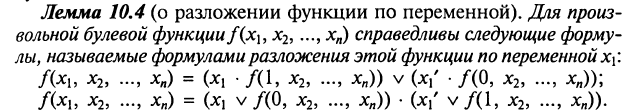
Представление булевых функций через конъюнкцию, дизъюнкцию и отрицание.

• 
  Всякая булева функция f(x₁, x₂, ..., x_n) может быть представлена в виде суперпозиции конъюнкции, дизъюнкции и отрицания; причем знак отрицания стоит только непосредственно около переменной и не стоит ни перед одной из внутренних скобок.
  

---

Системы булевых функций

Полные системы булевых функций

• 
  Система булевых функций называется полной, если всякая булева функция является суперпозицией функций из этой системы.
  

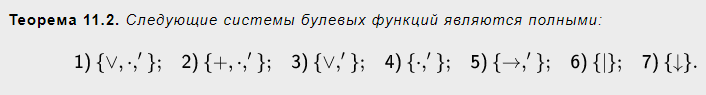
Специальные классы булевых функций

• 
  Говорят, что булева функция f(x₁, x₂, ..., x_n) сохраняет 0, если f(0,0, ...,0)=0. Обозначим P₀ — класс всех булевых функций, сохраняющих 0.
  

• 
  Говорят, что булева функция f(x₁, x₂, ..., x_n) сохраняет 1, если f(1,1, ...,1)=1. Обозначим P₁ — класс всех булевых функций, сохраняющих 1.
  

• 
  Булева функция f*(x₁, x₂, ..., x_n) называется двойственной функцией для булевой функции f(x₁, x₂, ..., x_n), если f*(x₁, x₂, ..., x_n) = f '(x'₁,x'₂, ...,x'_n) для любых x₁, x₂, ..., x_n. Булева функция f называется самодвойственной, если f* = f. Класс всех самодвойственных булевых функций обозначим S.
  

Иначе говоря, функция самодвойственна, если для произвольного набора значений аргументов отрицание всех переменных набора изменяет значение функции на противоположное. Для самодвойственной функции значения функции в столбцах, соответствующих противоположным наборам, например, (0,0) и (1,1), (0,1) и (1,0), будут противоположными (антисимметрия левой и правой частей таблицы).



Среди функций двух переменных классу S принадлежат функции f3, f5, f10, f12 (тождественно x, тождественно y, отрицание x, отрицание y).

• 
  Введем на множестве {0;1} отношение порядка, полагая, что 0 ≤ 0, 0 ≤1, 1 ≤1. Булева функция f(x₁, x₂, ..., x_n) называется монотонной, если для любых α₁, α₂, ..., α_n, β₁, β₂, ..., β_n ∈ {0;1} из неравенств α₁≤ β₁, α₂ ≤ β₂, ..., α_n ≤ β_n, немедленно следует, что f (α₁, α₂, ..., α_n)= f(β₁, β₂, ..., β_n). Класс всех монотонных функций обозначим M.
  

---