Файл: Нормальные формы для формул алгебры высказываний 1 Правила построения скнф по таблице истинности 2.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 96
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Нормальные формы для формул алгебры высказываний
Правила построения СКНФ по таблице истинности:
Правила построения СДНФ по таблице истинности:
Множества, отношения, функции в логике
Определение бинарного отношения
Выражение одних булевых функций через другие
Лемма о разложении функции по переменной
Полные системы булевых функций
Специальные классы булевых функций
Определение: Функцию f(x) = f(x1, x2, ..., xn) называют монотонной, если для любых двух сравнимых наборов и , таких, что ≤ , справедливо f(a) ≤ f(b).
. Для отнесения произвольной функции к этому классу необходимо сравнить ее значения на всех пяти парах сравнимых наборов:
(0,0) ≤ (0,1), (0,0) ≤ (1,0), (0,0) ≤ (1,1), (0,1) ≤ (1,1), (1,0) ≤ (1,1).
Среди функций двух переменных монотонными являются шесть функций: f0, f1, f3, f5, f7, f15 (тождественно 0, конъюнкция, тождественно x, дизъюнкция, тождественно 1).
-
Наконец, булева функция f(x1, x2, ..., xn) называется линейной, если ее можно представить в виде следующего выражения (называемого полиномом Жегалкина степени не выше первой):
f(x1, x2, ..., xn)= α0+ α1x1 + α2x2+...+ αnxn,
где α0, α1, α2, ..., αn — постоянные, равные либо 0, либо 1. Символом L обозначим класс всех линейных булевых функций.
-
Функция является линейной тогда, и только тогда, когда ее полином Жегалкина имеет степень не выше первой, т. е. содержит конъюнкции длиной не более 1. -
Свойство линейности переключательных функций определяется как свойство полинома Жегалкина, представляющего собой формулу над функциональным базисом, {∧, ⊕, 0, 1}. Рассмотрим вначале свойства операции ⊕:
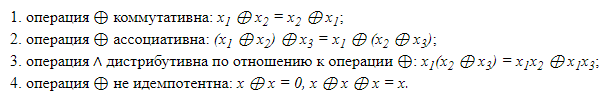
-
Для проверки произвольной функции на принадлежность классу L необходимо построить для нее полином Жегалкина. -
Среди функций двух переменных линейными являются 8 функций: f0, f3, f5, f6, f9, f10, f12, f15
Введенные классы булевых функций P0, P1, S, M, L играют главную роль при описании полных систем булевых функций. В следующей теореме устанавливаются два важных свойства этих классов и одновременно рассматриваются примеры функций, принадлежащих и не принадлежащих каждому из них.
Собственные замкнутые классы
-
Класс булевых функций называется собственным, если он не пуст и не совпадает с классом всех булевых функций. -
Класс булевых функций называется замкнутым или классом Поста, если он вместе со всякими своими функциями содержит любую их суперпозицию.
Теорема Поста о полноте системы булевых функций
-
Система булевых функций {f0, f1, ..., fs, ...} является полной тогда и только тогда, когда в этой системе имеется функция, не принадлежащая классу P0, имеется функция, не принадлежащая классу P1, имеется функция, не принадлежащая классу S, имеется функция, не принадлежащая классу M, имеется функция, не принадлежащая классу L.
Критерий Поста
Согласно критерию Поста, система булевых функций полна тогда и только тогда, когда она не содержится целиком ни в одном из классов P0, P1, S, M, L
В частности, если функция не входит ни в один из классов Поста, она сама по себе формирует полную систему. В качестве примера можно назвать штрих Шеффера или стрелку Пирса.
Широко известны такие полные системы булевых функций: {∧,∨,¬} (конъюнкция, дизъюнкция, отрицание); {∧,⊕,1} (конъюнкция, сумма Жегалкина, константа один).
Первая система используется, например, для представления функций в виде дизъюнктивных и конъюнктивных нормальных форм, вторая — для представления в виде полиномов Жегалкина.
Полином Жегалкина
-
Любая функция n переменных может быть представлена полиномом Жегалкина и это представление единственно.
Построение полинома Жегалкина с помощью таблицы истинности.
-
Построить СДНФ -
Все полученные конъюнкции нужно соединить знаками ⊕ -
Вместо всех отрицаний переменных x подставить эквивалентные подформулы (x ⊕ 1); -
раскрыть скобки и привести подобные члены по правилу: х ⊕ х ⊕...⊕ х ⊕ х = 0 (четное число слагаемых); х ⊕ х ⊕...⊕ х = x (нечетное число слагаемых).
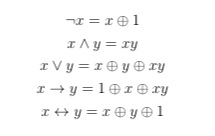
Представления функций