Файл: Определение отсчетного уровня для установления глубины портовой акватории.docx
Добавлен: 08.11.2023
Просмотров: 130
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Исполнитель: ________ Дуденко А.И.
Г-422 Проверил: профессор ________ Шматков В.А.
1.Определение глубины и ширины морского канала
2.Определение отсчетного уровня для установления глубины портовой территории
2.1.Статистические методы обработки уровенных наблюдений
2.2.Статистический метод расчета экстремальных уровней
3.Нахождение отсчетного уровня при коротком ряде наблюдений
3.1Связь между уровнями в двух пунктах
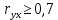. Если 
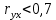, то необходимо искать другой опорный пункт.
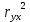– показывает, какая часть дисперсии переменной 
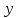полностью определяется переменной 
. 
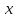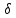– показывает разброс данных. 
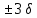– все значения укладываются в промежуток.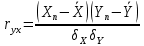
-
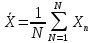
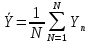
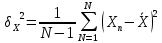
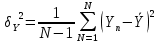
Величина коэффициента корреляции, вычисленная для конечного значения членов
ряда
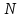представляет собой оценку истинного значения коэффициента корреляции (
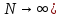. Следует определить вероятную и предельную ошибки.
Вероятная ошибка:
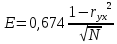
Предельная ошибка = 4E.
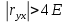
Практические нюансы вычисления коэффициента корреляции:
-
находим по коротким рядам наблюдений => полученную связь нельзя механически переносить на другие виды колебаний. -
Чем больше ряд, тем меньше ошибка. С увеличением длины ряда Е – уменьшается, увеличивается надежность коэффициента корреляции (только для независимых случайных величин). В нашем случае при обработке уровенных наблюдений увеличение длины ряда не всегда приводит к увеличению надежности (диссонанс сгонно-нагонных колебаний). -
Пункты А и Б выбирают по возможности близкорасположенными к друг другу и в одинаковых условиях (гидрометеорологических и морфологических условиях). В этом случае долгопериодные колебания в обоих пунктах будут проходить синхронно и коэффициент корреляции будет отображать связь именно этих колебаний. -
Коррелятивные связи должны оцениваться раздельно для различных видов колебаний.
Подготовка данных для приливных морей:
При изучении экстремальных значений уровней необходимо предварительно исключить приливные (периодические) колебания из наблюденных и найти связь только непериодических колебаний. Если эта связь хорошо выражена и так же хорошо выражена связь приливных колебаний, то можно рассчитывать коэффициент корреляции суммарных экстремальных уровней. При исследовании только непериодических колебаний приливные колебания исключаются, т.к. они коррелируются на больших расстояниях (до 100 км) - средние величины приливных колебаний гораздо больше величин непериодических колебаний.
1 2 3 4 5 6 7 8 9
3.2.Подбор пункта-аналога
В данной работе за исследуемый пункт взяли значения минимального среднемесячного уровня из исходной таблицы (Приложение 1). Для того чтобы определить пункт- аналог, необходимо провести предварительную графическую оценку (Приложение 3) и посчитать коэффициенты корреляции (табл.11.), затем выбрать наиболее подходящий пункт. Выбранный пункт есть пункт-аналог/опорный пункт.
Расчет коэффициентов линейной корреляции 12 пунктов Табл.11.
Из табл.2. видно, что наибольший коэффициент корреляции равен 0,61 в пункте №3. Также это подтверждается и графически (рис.13.)
Вероятная ошибка:
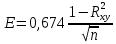= 0,07Предельная ошибка:
4Е = 0,28; ∣R xy ∣⩾4 ; 0,61⩾0,28
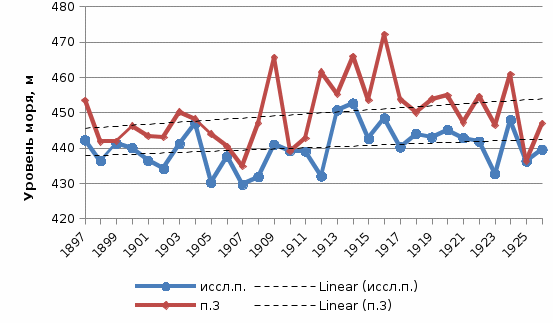
Рис.13. Среднегодовые значения уровня в исследуемом пункте и пункте №3 с 1897 по 1926 года
Следовательно, дальнейшие расчеты будут производиться для исследуемого пункта (значения минимального среднемесячного уровня) и пункта-аналога №3.
3.3.Вычисление коэффициента линейной корреляции
Коэффициент линейной корреляции показывает тесноту связей. В данном случае коэффициент линейной корреляции должен быть
. В работе, для нахождения коэффициента корреляции был использован следующий алгоритм: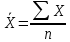
, 
, 
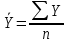
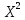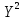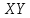
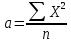
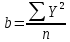
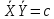
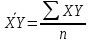
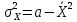
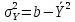
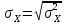
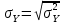
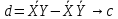
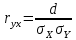
Сопоставление исследуемого пункта и пункта-аналога Табл.12.
| Год | Иссл. Пункт | п.3 | X2 | Y2 |
| 1897 | 442,2 | 453,5 | 205662,25 | 195540,84 |
| 1898 | 436,3 | 441,8 | 195187,24 | 190357,69 |
| 1899 | 441,2 | 441,9 | 195275,61 | 194657,44 |
| 1900 | 440 | 446,2 | 199094,44 | 193600 |
| 1901 | 436,4 | 443,4 | 196603,56 | 190444,96 |
| 1902 | 434,1 | 443 | 196249 | 188442,81 |
| 1903 | 441,1 | 450,2 | 202680,04 | 194569,21 |
| 1904 | 447 | 448,2 | 200883,24 | 199809 |
| 1905 | 430,2 | 444 | 197136 | 185072,04 |
| 1906 | 437,6 | 440,4 | 193952,16 | 191493,76 |
| 1907 | 429,6 | 434,8 | 189051,04 | 184556,16 |
| 1908 | 431,8 | 447,1 | 199898,41 | 186451,24 |
| 1909 | 440,9 | 465,6 | 216783,36 | 194392,81 |
| 1910 | 439,1 | 439,1 | 192808,81 | 192808,81 |
| 1911 | 439 | 442,7 | 195983,29 | 192721 |
| 1912 | 432 | 461,5 | 212982,25 | 186624 |
| 1913 | 450,7 | 455,2 | 207207,04 | 203130,49 |
| 1914 | 452,6 | 465,9 | 217062,81 | 204846,76 |
| 1915 | 442,6 | 453,6 | 205752,96 | 195894,76 |
| 1916 | 448,4 | 472,2 | 222972,84 | 201062,56 |
| 1917 | 440,2 | 453,7 | 205843,69 | 193776,04 |
| 1918 | 444 | 450 | 202500 | 197136 |
| 1919 | 443 | 453,9 | 206025,21 | 196249 |
| 1920 | 445,1 | 454,8 | 206843,04 | 198114,01 |
| 1921 | 442,8 | 447,2 | 199987,84 | 196071,84 |
| 1922 | 441,8 | 454,5 | 206570,25 | 195187,24 |
| 1923 | 432,6 | 446,4 | 199272,96 | 187142,76 |
| 1924 | 447,9 | 460,9 | 212428,81 | 200614,41 |
| 1925 | 436,2 | 436,2 | 190270,44 | 190270,44 |
| 1926 | 439,5 | 447 | 199809 | 193160,25 |
| Σ | 13205,9 | 13494,9 | 6072777,59 | 5814198,33 |
| среднее | 440,20 | 449,83 | 202425,92 | 193806,611 |
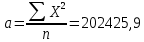
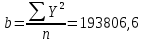
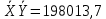
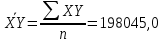
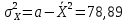
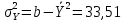
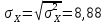
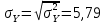
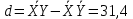
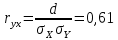
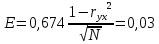
Предельная ошибка
; 
(
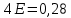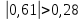)Так как коэффициент линейной корреляции находят по коротким рядам наблюдений, то полученную связь нельзя переносить на другие виды колебаний уровня.
С увеличением ряда наблюдений уменьшается ошибка определения коэффициента линейной корреляции, т.е. увеличивается надежность наблюдений, но только для математически независимых величин.
Для приливных морей при изучении max и min уровней необходимо предварительно исключить приливные колебания из наблюденных.
1 2 3 4 5 6 7 8 9
3.4.Нахождение уравнения регрессии
Уравнение связи имеет вид:
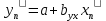
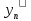– оценка высоты уровня в исследуемом пункте
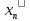– высота уровня в опорном пункте. 
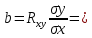0,35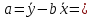
280,77Уравнение связи примет вид:
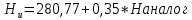
Средняя ошибка уравнения регрессии
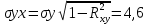
Подставляем в уравнение связи минимальный и максимальный уровни опорного пункта. По полученным данным строим график. На графике откладываем ошибку, чтобы посмотреть, сколько значений попадает в интервал, а сколько не попадает (рис.14.).
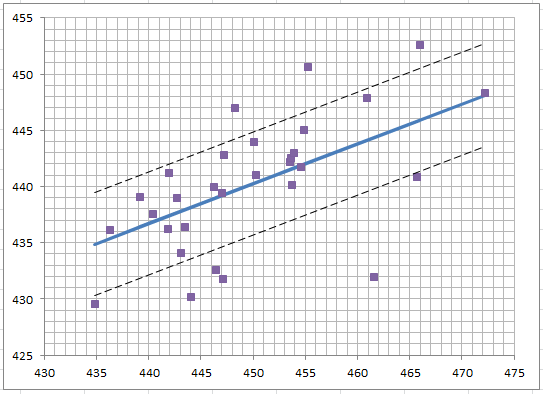
Рис.14.График регрессии
Как видно в интервал попало 21 из 31 уровней. Это соответствует 70%.
Заключение
Для обеспечения дноуглубительного уровня портовой акватории проделывается большая работа по нахождению и изучению материалов, полученных за большие периоды времени.
Губа Кереть находится в приливном море, поэтому наблюдения должны вестись не менее 3 лет, причем наблюдения ежечасные.
При этом установленный уровень (отсчётный) находится на отметке в 98% (а это значит, что в 2% случаев уровень будет меньше).
Это в случае, если на конкретной акватории имеется ряд долгосрочных наблюдений. В противном случае находится пункт-аналог, расположенный в схожих гидрометеорологических условиях, затем устанавливается связь между 2 пунктами, однако уравнение связи имеет ошибку (которую следует учитывать).
В данной работе был назначен отсчётный уровень портовой акватории п. Брест3 с обеспеченностью в 98%, равный: