Файл: Алпысов А.. Математиканы оыту дістемесі оу ралы Павлодар, 2012.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 1767

Скачиваний: 140

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Алпысов А.Қ.

1. Математиканы оқыту әдістемесі пәні

2. Математиканы оқытудың мақсаттары мен мазмұны

Математиканы оқытудың қағидалары

Математиканы оқытудың әдістері

5. Математикалық ұғымдар, сөйлемдер және оларды үйренудің әдістемесі

6. Математиканы есептер арқылы оқыту әдістемесі

Математикадан сыныптан тыс жұмыстар, оны өткізу әдістері

9. Педагогикалық практика туралы

10. Геометрияны оқыту әдістемесі Планиметрия курсын үйрену әдістемесі. Геометрия есептерін шешудіңәдістері. Стереометрия курсын үйренуәдістемесі. Геометрияны оқытуда есептерді шеше білу дағдысын қалыптастыру және оны жалпы түрде дамыту аса маңызды мәселелердің бірі болып табылады. Геометриялық есептерді шешу туралы жалпы білік- дағдылар әдетте көптеген есептерді шешу арқылы қалыптасады. Олай болса, студент пен оқытушының не мұғалім мен оқушының жүйелі түрде ұзақ уақыт еңбектенуіне тура келеді. Шешілу жолы беймәлім, әр түрлі теориялық фактілерді байланыстыруды қажет ететін, студенттер шығара алмайтын жаңа есептер де жиі кездеседі. Сондықтан студенттерді кез келген геометриялық есепті шешудің жалпы тәсілдерімен қаруландыру керек. Бұл талап математикалық есептерді шешу практикумының бағдарламасында да айтылған. Практикум белгілі бір есептердің түрлерін және оларды шешудің тәсілдерін таныстыруға бағытталып қана қоймай, қайта дәлелдеудің барынша жалпы әдістерін ойлауды меңгерту болып табылады. Оқытушы студентке әрбір есепті шығартқанда, оның шешімін әдістемелік талаптарға сай іздеуге, соңында мақсатқа сай дұрыс шешімді табуға жәрдемдесетіндей талдау тәсілдері мен болашақ мұғалімдерге қажетті білім-білік дағдыларын қалыптастыруға ұмтылады. Теориялық және әдістемелік білім мен әдіс- тәсілдерінсіз кез-келген әдістемелік есепті шешуге бола бермейді. Практикадан байқалатындай, көбінесе геометрия есептері әр түрлі тәсілдермен логикалық тұрғыда көбірек ойлануды қажетсінеді. Геометрия есептерін шешудің кезеңдерін білу оқушылар мен студенттерде қалыптастырылуға тиісті аса маңызды дағдылардың бірі. Есептерді шешу процесі келесі кезеңдерден тұрады. Есептің шартын түсіну: а) есепті талдау; б) есеп шартын схема түрінде жазу. Есепті талдағанда оның шарты қандай, онда қандай талап қойылған (не берілген, не белгілі, есеп шарты неден тұрады?) екені анықталады. Есеп шартын схема түрінде жазғанда оның сызбасы қоса қарастырылады, осы талдаудың нәтижесінде есеп шартындағы ең керекті, таныс элементтер ескеріліп, олар қысқаша жазылады. Есепті талдау мен оның сызбасын және шартын схема түрінде қысқаша жазу — есепті шешу үшін жоспар іздеудің негізгі құралы болып табылады. Есепті талдай келе осы есепке қандай мөлшерде теориялық білімнің қажет болатындығы анықталады. Есеп шешімін іздеу — есепті шешудің тәсілін іздеу, бұл бүкіл процестің негізгі бөлігі болып табылады. Бұл кезеңде ең алдымен берілген есептің түрі (типі), яғни оның дәлелдеуге, есептеуге не геометриялық түрлендіруге берілгені анықталады, осыған орай есепті шешу тәсілі ізделеді. Есеп шартында берілген элементтер мен іздеуге, анықталуға тиісті белгісіздер арасындағы байланыс ізделеді. Есеп шешімін іздеуде бір-бірімен тығыз байланысты мынадай екі жақты мәселені анықтайды: а) белгілі теориялық білімді шешілуге тиісті есеп шартына сай түрлендіру; б) есеп шартын белгілі теориялық фактілерге сәйкес және оларға байланысты түрлендіру. Бұл арада теориялық білім деп отырғанымыз математикалық ұғымдар мен олардың анықтамалары, теоремалар және математикадағы негізгі әдістер (координаттар әдісі, векторлық әдіс, геометриялық түрлендірулер мен теңдеулер құру әдісі және т.б.). Есептердің түрі мен құрылысына қарай оларды кластарға жіктеп талдау мен шешу әдістерін таңдап алады. Әсіресе, бірнеше теориялық материалдарды біріктіретін, әрі күрделі, әрі көптеген есептерді шешуге теориялық әдістемелік негіз болатын тірек есептерін талдау кезінде белгілі бір гипотеза ұсынылады және оның іске асырылуы тексеріледі. Есеп шешімін іздеу үшін гипотеза ұсына отырып, осы есепке нақтылы қандай теориялық материал керек болатынын анықтаймыз. Теориялық білімді негіздеуші әдісті таңдап, гипотезаны тексереміз. Егер есепті талдағанда бұрыннан таныс элементті байқасақ, не ол шешілуі таныс есепке ұқсас болса, онда есепті шешу үшін белгілі әдісті қолдану мүмкіндігі туралы ой, не есепті шешу жоспары пайда болады. Егер есептің таныс емес түрін шығаруға тура келсе, онда одан бұрыннан таныс есептердің кемінде бір элементін іздейміз немесе берілген есеп шартын бұрын шешілген есептегі таныс бір элемент табылатынын талдаймыз. Жоспарды іске асыру. Бұл арада шешу идеясы табылып, есеп шешіледі. Шешілген есепті талқылау: а) есеп шешімін тексеру; б) есепті зерттеу; в) есеп шешімін әр түрлі параметрлер мен байланыстар бойынша талдау. Есептің шешілуінің және оған қолданылған әдістер мен теориялық негіздеулердің дұрыс екенін, ол шешім есеп шартының барлық талаптарын қанағаттандыратынын білу үшін оны тексеру керек. Есепті зерттеу келесі мәселелерді анықтауы керек: қандай шарт орындалғанда есептің шешімі бар; қандай шарт орындалғанда есептің жалпы шешімі жоқ болады?Есептің шешімін талдау мынадай мәселелерге жауап береді. Есепті шешудің бұдан басқа ең тиімді жолы жоқ па? Есепті жалпылауға бола ма? Осы есептен қандай қорытындылар жасауға болады? Есепті шешу процесінің құрылымы ең алдымен есептің сипатына, есеп шығарушының қандай біліммен, білікпен, дағдымен қаруланғанына тікелей байланысты. мысал. Тікбұрышты үшбұрыштың катеттеріне жүргізілген медианаларысм жәнесм. Оның гипотенузасын табу керек (8-сурет). А ЕС ВF8-суретШешуі. ВС мен AC катеттерін сәйкес х пен у ар-ылы белгілейік. ВСЕ, ACF — тікбұрышты үшбүрыштар болғандықтан,ВС 2  BE 2  EC 2және CF2 AF 2 AC 2 , яғни x2 2  y73  4жәнеx  52  y2 24 . Бұл тендеулер жүйесін шешіп, х пен у-ті табамыз: 73  0,25y2  4  52  4y2 ,y2  36 ; y  6cм ,х  8см;АВ  10см . мысал. ABC үшбұрышында АВ=26см, BC=30см, АС=28см. В төбесінен ВН биіктігі мен BD биссектрисасы жүргізілген. BHD үшбұрышының ауданын табу керек. Шешуі. ABC үшбұрышының ауданын екі әдіспен өрнектейік: SAВС 0,5АС  ВН 0,5  28  h  14h ; екінші жағынанS АВС  336см2 . Демек, 14h=336, h=24 см. Енді CD=x деп алып, ABC үшбұрышының ішкі бұрышы биссектрисасының қасиетін пайдаланайық: ВС:АВ=CD:DA, 30:26=x:(28-x), х=СD=15см; AD=28-15=13см. ВСН : СН 2  ВС 2  ВН 2  324, CH=18 см, DH=CH-CD=18-15=3см, S=0,5DH  ВН 36см2 . мысал. Медианалары mb  9см ,ma  12см ,mc  25смболатын үшбұрыштың ауданын есептеу керек (9-сурет). СА сурет Шешуі.ABC : mb  BE  9см ,ma  AD  12см .mc  CF  15см. Берілген элементтер мен іздеген элементтің арасындағы байланысты анықтайық (О — медианалардың қиылысу нүктесі). AOC : AО  2 m  2 12  8см , OC  2 m 10см , OE  1 m 3см 3 a33 с 2 b ОЕ медианасын екі еселеп, АОС үшбұрышын AOCB1параллелограмына дейін толықтырайық. Сонда AC 2  OB2  2(AO2  OC2 ) ; AC . Осы сияқты OD медиананы екі еселеп, ВОС үшбүрышынпараллелограмға толықтырсақ: BC   .Осылай қарастырып, АВ=10см екенін аламыз. Енді Герон ABCформуласымен ауданды есептесек, S  72см2 . Осы есепті басқа әдіспен шешейік.AOC менABC -ның табандары тең болғандықтан, S 1 SШынында да,OME BNE ,OM  OE , алOE  1 AOC3 AOCBN BEBE 3 болғандықтан,OM  1 . СондықтанBN 3 SAOC SABC OMBN 1 ,3SAOC 1 S3ABC ЕндіAOCB1параллелограмынан: 1SAOC  SOCB ; OC  2 EC  2 15  10 , CB  AO  2 m  8, OB  2OE  2  1  9  6 , AOC ABC3 3 1 3 a 1 3 p  12 ,S  24см2 ,S  72см2 Геометрия есептерін шешудің әдістеріне: а) геометриялық; б) алгебралық; в) комбинациялық деп аталатын негізгі әдістер жатады.Есептерді геометриялық әдіспен шешкенде логикалық ойлаудың жәрдемімен белгілі теоремалар арқылы тұжырымдауды қажетсінетін сөйлемдерді дәлелдейміз. Ал есептерді алгебралық әдіспен шешкенде ізделінген шаманы табу, не тұжырымдауға тиісті сөйлемді дәлелдеу тікелей есептеу жолымен немесе теңдеулер мен олардың жүйелерін құру арқылы іске асады. Тікелей есептеу әдісінің мәні мынада: есептің берілгендері мен белгісіздерінің жан-жақты байланыстарынан аралық қосымша белгісіз шамалар тізбегі құрылады, тізбекке қатысытын әрбір белгісіз шама анықталады немесе іздеген шама белгілі шамалар арқылы өрнектеледі. - мысал. Теңбүйірлі ABC үшбұрышының табаны AC, төбесіндегі В бұрышы сүйір, С бұрышының биссектрисасы CD кесіндісі болсын. D нүктесі арқылы CD биссектрисасына перпендикуляр түзу жүргізілген. Бұл түзу үшбұрыштың AC табанымен немесе оның созындысымен Е нүктесінде қиылысады. AD =0,5ЕС болатынын дәлелдеу керек (10-сурет). ВFDЕ А K С сурет Есеп геометриялық әдіспен тікелей шешіледі. CD кесіндісі — EFC үшбұрышының әрі биіктігі, әрі биссектриссасы. D нүктесін ВС қабырғасымен (CD  EF және CD — С бұрышының биссектриссасы) қиылысқанша созсақ, EFC теңбүйірлі үшбұрышы шығады. Есептің шарты бойынша CD  EF. Ендеше ED = DF. D нүктесінен ВС-ға параллель түзу жүргізсек, ол AC табанымен К нүктесінде қиылысады. Бұл DK кесіндісі EDC үшбұрышының медианасы бола алады. ЕК:КС = ED:DF = 1, бұлардан DK = 0,5ЕС, сондықтан AD = DK= 0,5 EC. -мысал.Теңбүйірлі трапецияға іштей дөңгелек сызылған. Трапеция ауданының дөңгелек ауданына қатынасы -ге тең. Трапецияның үлкен8 табанындағы сүйір бүрышын табу керек (11-сурет). ABCD — теңбүйірлі трапециясы берілген,Sдон : STP  : 8 . Бірінші тәсіл. Есептің мазмұнынан оны синтез әдісімен немесе алгебралық әдіспен шешуге болатынын байқаймыз. Синтез әдісі бойынша берілгендерге сүйеніп дөңгелектің радиусын табуға болады. Дөңгелектің радиусын г, трапецияның табан қабырғалары ұзындықтарын a, b деп қосымша белгісіздер ендіреміз. Есеп шарты бойынша r 20,5(a b)  2r  , 8a b 8r,r  a  b .8 Екінші жағынан шеңберді сырттай сызылған төртбұрыштың қасиеті бойынша AD+BC=AB+DC теңдігін жаза аламыз. Бұдан 2AD=a+b, AD=0,5(a+b). Тікбұрышты AED үшбұрышынанsin A  DE AD4r a  b; бұл теңдікке r-дің мәнін қойып ықшамдасақ, sin A = 0,5 шығады. Сонымен,A  .6 A BE сурет Бұл есепте жоғарыда айтылған тірек элементін және қосымша белгісіздер енгізу, теңдеу құру, қосымша белгісіздерді ығыстыру процестерінің барлығы орындалады.Екінші тәcіл. 11-суреттен AD=BC теңдігін ескеріп, бір нүктеден шеңберге жүргізілген екі жанама тең болатынын пайдалансақ, AN  a ,2NN  b,2sin A  DEAD2r AN  ND4r .a  b r-дің 1-тәсілдегі мәнін орнына қойсақ, sinA = 0,5, бұданA  .6 Теңдеулер құру арқылы шешілетін есептерді қарастыралық.6-мысал. Тікбұрышты үшбұрыштың гипотенузасы с-ға тең, үшбұрыштың бір сүйір бұрышынан катеттерінің біріне ұзындығы m-ге тең медиана жүргізілген. Осы үшбұрыш катеттерінің ұзындықтарын табу керек (12-сурет). ВDС А12-сурет Есепті теңдеу құру әдісімен (алгебралық әдіспен) шешу үшін АС=x, BC=y деп белгілейік. Тікбұрышты үшбұрыштардан Пифагор теоремасы бойынша:АС 2  ВС 2  AB 2 ,АС 2  СD2  AD2немесеx2  y2  c2 , x2 (0,5y)2 m2 . Бұл жүйенің шешіміBC  2, AC . Математикалық есептердің көбінде қосымша белгісіздер енгізу әдісі қолданылады. Бұл есептердің берілген элементтері мен қажетті теориялық материалдарды байланыстыруға септігін тигізеді. Есепті шешу барысында осы қосымша белгісіздер ығысады.7-мысал. Ромб биіктігі оның қабырғасын m және n бөліктерге бөледі.Ромб диагоналдарының ұзындықтарын табу керек (13-сурет). СА13-сурет тәсіл. Теңдеулер құруға қажетті белгісіздер енгізелік. Ол үшін АС=x, BD=y деп белгілейміз. СондаАВ  AE  EB  m  n.Бұл қосымша элементті есеп шартындағы белгілі және белгісіз шамалар арқылы өрнектейміз. ЕD  h десек,h2  y2  n2жәнеh2  (m  n)2  m2.h2 -тың мәндерін теңестірсек, у2  n2  (m  n)2  m2, х-ті табамыз:y 2  2mn 2n2немесеy . АОВ үшбұрышынан АО2  AB2  OB2  (m n)2  (0,5 AC  x  2AO 2n(m  n))2 ,. Сонда жауабы: 2n(m n), . тәсіл. Аудандарды пайдалану әдісі бойынша 0,5d1d2шамасын қосымша элементтер арқылы табылатын ауданға теңестіреміз, яғни 0,5d1d2  (m  n)2n(m  n) , мұндағыh 2n(m  n) . АОВ үшбұрышынан (0,5d )2  (0,5d )2  (m n)2 немесе d 2  d 2  4(m  n)2 . Бірінші теңдіктің екі1 2 1 2 жағында 4-ке көбейтіп екінші теңдікке қоссақ, онда 1 2(d  d )2  4(m  n)  4(m n)2  4(m n)( m  n). Бірінші теңдіктен d1 -ді тапсақ және оны соңғы теңдікке қойсақ, түрлендіргеннен кейінd  болады. Енді d 2  4(m  n)2  d2 2 1 1 теңдігінеd 2 -нің табылған мәнін қойсақ,d1  екені шығады. Егер берілген есепте кейбір шамалардың (ұзындықтардың немесе аудандардың) қатынастарын табу қажет болса, дербес жағдайда белгілі бір бұрышты есептеу қажет болса, ондай есептер көмекші параметр енгізу деп аталатын тәсілмен шешіледі. Бұл тәсіл бойынша есепті шешу үшін сызықтық элементтердің біреуін белгілі деп алып, іздеп отырған шаманы сол арқылы өрнектейді де олардың қатынастарын құрады. Мектеп оқушыларының кеңістікті қабылдап, оны көз алдына елестете алуы стереометрияны оқытудың негізгі мәселелерінің бірі болып саналады. Осы айтылған мақсатты іс жүзіне асыруда кеңістіктегі салуға берілген есептерді шешудің зор мәні бар. Жазықтықтағы геометриялық салулар теориясы жеткілікті түрде талқыланып қарастырылады, ал стереометрияның әдістемелік мәселелеріне әлі де толық көңіл бөлінбей келеді. Геометриялық салулар теориясы – салуды негіздеу, есептерді кластарға жіктеу, есеп шешу әдістері, белгілі бір класқа жататын есептерді шешу критериі, салу есептерін шешкенде барынша жай әдістерді тиімді қолдану сияқты мәселелерді қарастырады. Кеңістіктегі салу есептерін кластарға жіктеу туралы әр түрлі көзқарастар мен тәсілдер бар. А.Н. Чалов кеңістіктегі салу есептерін геометриялық салуды орындау тәсілдері бойынша келесі топтарға бөледі: 1) елестету арқылы шешілетін есептер; 2) проекциялық сызбамен шешілетін есептер; 3) модельмен шешілетін есептер. Салуға берілген стереометрия есептерін позициялық және метрикалық деп екі топқа бөлетіндер де бар. Негізгі элементтерінің қиылысуын ғана іздейтін, соны салумен аяқталатын есептер позициялық әдіспен шешілетін есептерге жатады. Кесінді салу, белгілі бір шамасы бар бұрышты салу, перпендикуляр тұрғызу, биссектриса жүргізу және т.б. белгілі шарттарды қанағаттандыратын фигура салу талабы қойылатын есептер метиркалық есептерге жатады. Мысалы, В.А. Гусев, В.Н. Литвиненко, А.Г. Мордкович өздерінің құрастырған «Математикалық есептер шешу практикумында» кеңістіктегі салуға берілген есептерді мынадай әдістер бойынша топтарға бөледі: 1) кеңістіктегі қарапайым салулар; 2) нүктелердің геометриялық орындары; 3) кейбір нүктелердің геометриялық орындары мен түзулерді пайдалану; 4) кескіндеу арқылы салу.Салуға берілген стереометрия есептері талдау, салу, дәлелдеу жәнезерттеу сияқты төрт кезеңнен тұрады.Талдау – бір бүтінді, құрамды бөліктерге жіктейтін, әр бөлікті жеке қарастыратын зерттеу әдісі. Ол салу есебін шешудің жоспарын табуға мүмкіндік тудырады. Талдау – есеп шешудің барынша маңызды кезеңі. Есепке дұрыс жүргізілген талдау – есепті шешу жоспарын дұрыс құрастырудың кепілі. Салу есебіне талдау жасағанда сызба басты рөл атқарады. Сонда есеп шартын, сызбадағы элементтердің өзара орналасуына барынша басынан аяғына дейін талдау жасалады, есеп шартында берілгендер мен іздеген элементтер арасында байланыс орнатылады. Есептің салу кезеңінде салу есебіне қолданылатын аксиомаларды, теоремаларды, қосымша қарапайым салуларды дәл көрсету керек. Дәлелдеу кезеңі есеп шешімінің дұрыстығына күдік туғанда қажет болады. Салу есебін зерттеу кезеңінің өзіндік маңызды ерекшелігі бар. Ол қандай шарттар орындалғанда есептің шешуі бар болады және неше шешімі бар деген сұрақтарға жауап береді. Сонымен бірге зерттеу кезеңі кеңістік елесті дамытуға мүмкіндік туғызады.Салуға берілген алғашқы есепті шығарғанның өзінде есепті шешудің кезеңдерін (талдау, салу, дәлелдеу, зерттеу) дәл анықтап бөлу керек.Кеңістіктегі салуға берілген есептерді шешудің негізгі әдістері:аксиоматикалық әдіс, проективтік әдіс, геометриялық орындар әдісі.Аксиоматикалық әдістің негізгі мәні есепті шешу кезінде салудың өзі орындалмайды, салуға берілген есеп элементар салуларға келтіріледі, кейін бұлардың бәрін бірге қарастыруға болатындай түрдегі барлық жай амалдар қарастырылады. Салу есебінде көрсетілген амалдар кейде аксиомалар деп, ал есепті шешу әдісі аксиоматикалық әдіс деп аталады. Себебі есепке қолданылатын барлық амалдар елестеу арқылы формальді түрде жүргізіледі де логикалық түрде негізделеді, мұндай әдіс формальді-логикалық әдіс деп те аталады. Әдетте логикалық ой тұжырымдары сызба арқылы жүрізіледі. Бұл есеп шешімін барынша жеңілдетеді: ойды іске қосады, көптеген геометриялық элементтер мен олардың жиынын есте сақтап қалуға, кеңістік жөнінде дұрыс түсінік орнығып қалыптасуына мүмкіндік берді. Аксиоматикалық әдіс оқушылар санасында кеңістік туралы түсініктің, логикалық ойлаудың дамуына барынша терең және берік теориялық білім алуға, әсіресе белгілі бір салуларға түсінік беретін стереометрияның алғашқы теоремаларын үйренуге мүмкіндік туғызады. Есептер шешу кезінде алдымен көрнекі құралдар – жазықтықтар моделі (нұсқасы), нүктелер мен түзулерді мақсатты түрде қолдану пайдасы зор. Осындай әдістер көмегімен салудың талаптары айқын түрде көрсетіледі, бұдан соң логикалық түрде негіздеу және логикалық негізде салынған кескінді салу дәлелденеді. Модельдеу есеп шешімін көрнекі түрде талдау жасауға, талдауды ықшамдауға мүмкіндік береді.Проективтік әдіс (проекциялық сызбада салу есебін шешу әдісі). Егер ерекше проекциялау ережесі бойынша геометриялық денелердің кескінін пайдалануға мүмкіндік болса, онда ол есепті сызбалық құралдың көмегімен барлық салу жұмысын орындауға болады. Мұндай кескін геометриялық денені бір жазықтыққа проекциялау жолы мен алынады және проекциялық сызба деп аталады, ал есепті шешу әдісін «проекциялық сызбада салынатын есеп» деп атайды.Кеңістіктегі салу есептерін шешуге барынша ынғайлы әдіс – еркімізше алынатын параллель проекциялау. Ол сызбаның көрнекілігімен, оны салудың өте жай қарапайым болатынымен сипатталады. Проекциялық сызба арқылы шешілетін салу есептері төрт кезеңнен тұрады. Бірақ барлық кезеңдерді әр есепте түгел іске асыру талабы қойылмайды.Геометриялық орындар әдісі. Кеңістікте элементтердің геометриялық орындарын табуға берілген кез келген есепті салу есебі ретінде тұжырымдауға болады. Кеңістіктегі геометриялық орындар әдісімен салуға берілген есептерді шешудің мәні төмендегі мәселелер арқылы сипатталады. Әуелі есептегі берілген шарттардың біреуінен басқасын ескерусіз қалдыра тұрамыз. Өзіміз әдейі таңдап алып қалаған бір ғана шартты қанағаттандыратын нүктелер жиынын қарастырамыз. Бұдан әрі есептің екінші шартын қанағаттандыратын нүктелер жиыны қарастырылады жәнет.с.с. Біз қарастырған барлық жиындардың қиылысуы есептің шешімі болады. Кеңістіктегі салу есептерін шешудің тек төрт әдісін қарастырдық. Кеңістікте салуға берілген есептерді шешудің басқа да әдістері бар. Есептер шешудің бір немесе басқа әдісін таңдап алу шешілуге тиісті есептің сипатына, есеп шығарушының дайындық дәрежесіне, т.б. байланысты. Күрделі есептерді шешу кезінде көбінесе бір мезгілде бірнеше әдіс қатарынан қолданылады.Кеңістіктегі салуға берілген есептерді шешуге мысалдар қарастырайық. мысал. Берілген а және b түзулеріне паралелль, берілген А нүктесінен өтетін жазықтық жүргізу керек. Талдау. Іздеген жазықтық а түзуіне паралелль а1түзуі арқылы өтуі керек. Дәл осы сияқты іздеген жазықтық b түзуіне паралелль b1түзуі арқылы өтуі керек. а1және b1түзулері А нүктесі арқылы өтуі керек. Салу. 1. А нүктесі және а түзуі арқылы жазықтығын жүргіземіз. 2.  жазықтығында А нүктесі арқылы а түзуіне паралелль а1түзуін жүргіземіз. 3. А нүктесі және b түзуі арқылы жазықтығын жүргіземіз. 4. жазықтығында А нүктесі арқылы b түзуіне паралелль b1 түзуін жүргіземіз. 5. а1 және b1түзулерінен бір-бірден М және N нүктелерін таңдап аламыз. 6. А, М, N нүктелері арқылы іздеген а жазықтығын жүргіземіз. Дәлелдеу. 1. Салуымыз бойыншаа1 ажәнеа1 . яғни,а . 2. b1 b -бұл салуымыз бойынша жәнеb1 . Демек,b . 3.A a1жәнеA  b1 . сонда, A.Зерттеу. А нүктесінің а немесе b түзулерінде жатуына тәуелсіз есептің әрқашан шешімі болады. Егер а мен b түзулері паралелль болмаса, онда есептің бір ғана шешімі бар болады. Ал көп шешуі бар болады.а bболса, онда есептің сансыз мысал. Барлық төрт қабырғасы және қарама-қарсы екі қабырғасының орталарын қосатын кесінді берілген жағдайда ABCD төртбұрышын салу керек (14-сурет). D СC114-суретШешуі. ABCD — ізделген тертбұрыш, EF — АВ және DC қабырғаларының орталарын қосатын кесінді болсын. AD қабырғасын параллель жылжытыпED1және ВС қабырғасын параллель жылжытыпEC1 жағдайына келтіреміз, сондаDD1  AE ,DD1AE ; CC1  BE ,CC1BE , DF  CF — бұлар шарт бойынша, демек,DD1 F  FC1C(екі қабырғасы және олардың арасындағы бұрышы бойынша тең). Бұл үшбұрыштардың теңдігінен DFD1  CFC1шығады. Демек,D1 , F жәнеC1 — нүктелері бір түзудің бойында жатады.D1 EC1үшбұрышында екі қабырғасы мен үшінші медианасы белгілі болғанда оны салуға болады. Бұдан соң үш қабырғасы бойынша DD1 F жәнеFCC1үшбұрыштарын салып,DAED1 , жәнеBEC1C параллелограмдарын салуға болады. Бұдан соң A және В нүктелері анықталады. Салу.DEC1үшбұрышынD1 E  ADжәнеCE1  BC, сондай-ақ EF медианасы бойынша саламыз. Бұл үшін ең алдымен 2EF,ED1 ,EC1 , үш қабырғасы бойынша үшбұрыш салып, оны параллелограмға дейін толықтырамыз. Осы параллелограмның жартысыD1 EC1 — үшбұрышы болады. Қабырғалары1 DC2және1 AB2болатын өзара тең үшбұрыштарD1 F жәнеFC1кесінділеріне салынады. Бұлар арқылы D және С нүктелерін саламыз.DAED1жәнеBEC1Cпараллелограмдарын салып, А және В нүктелерін табамыз.Дәлелдеу. ABCD төртбұрышы — ізделген төртбұрыш, себебі ол есептің барлық шарттарын қанағаттандырады. DF және FC бір түзудің бойында жатыр, себебіDFD1  CFC1 жәнеDF1 және C1 Fбір түзудің бойьшда жатыр. Зерттеу.ED1C1 үшбүрышын салу үшін2EF  AD  BCжәне 2EF AD  BCшарттарының орындалуы қажетті, алDD1 FжәнеFCC1 — салу үшінD F  1 ( AB CD) және D FAB  CDшарттары орындалуы 1 2 1қажетті. Егер бұл шарттар орындалса, онда есептің бір ғана шешімі бар болады.Әдістемелік ұсыныстар: 1. Кеңістікте салуға берілген есепті шешуге кірісуден бұрын материалдың теориялық жағын меңгеріп алу қажет. 2. Салу есептерін шешуге кіріскенде алдымен қарапайым салулардан бастап шешу керек. 3. Есептер шешу кезінде әсіресе көрнекі құралдар мен модельдерді (нұсқаларды) пайдаланудың ерекше маңызы бар. 4. Негізгі салуларды дәл орындау керек: а) кеңістіктегі нүктенің орнын анықтау; б) берілген екі нүкте арқылы түзу жүргізу; в) бір түзудің бойында жатпайтын үш нүкте арқылы жазықтық жүргізу; г) түзу мен жазықтықтың қиылысу нүктесін табу; д) әрбір жазықтықта барлық планиметриялық салулардың орындалуы; е) егер өзін анықтайтын элементтер берілсе, онда геометриялық дене салу.Егер кеңістікте салуға берілген есептердегі негізгі амалдар, яғни онда ұсақ бөліктерге бөлінетін негізгі қарапайым салулар түгел орындалса, онда кеңістіктегі кез-келген геометриялық салу орындалады деп есептеледі. 1   ...   6   7   8   9   10   11   12   13   ...   16

Практикалық сабақтар

Математиканы оқыту әдістемесі пәні бойынша тест сұрақтары

Тест сұрақтарының жауаптары

Әдебиеттер

Алпысов Ақан Қанапияұлы


Оқу материалының түсініктілігі оның күделілігіне, оқушылардың даму ерекшеліктері мен дайындық деңгейіне, білімді саналы меңгеруге көмектесетін оқыту әдістері мен құралдарының орынды қолданылуына байланысты.

Математикамен бала күннен бастап қоректеніп, оның бұлтартпайтын дәлел- демелерін бойына молынан сіңірген адам ешбір алдамышқа оңайлықпен жол бермейтін шындықты қабылдауға дайынтұрады.

Гассенди П.


  1. 1   2   3   4   5   6   7   8   9   ...   16

Математиканы оқытудың әдістері




    1. Оқыту әдістері және оның түрлері.


    2. Математиканы оқытудың ғылыми әдістері.




    1. Математиканы оқыту процесінде оқушылардың жас ерекшеліктері мен пәннің мазмұнына сәйкес таңдалған оқыту әдістері білімнің саналы да, баянды болуын көздейді. Әдіс ең кең мағынада – мақсатқа жету тәсілі, белгілі бір тәртіппен реттелген қызмет. Оқу процесінде оқыту әдісі оқушы мен мұғалімнің арасындағы тиімді қарым–қатынастың бір түрі.

Оқыту әдісі деп оқушылардың белсенді танымдық қызметін қамтамасыз ететін, мұғалім мен оқушының бірлескен әрекеттерінің нақты түрі. Оқыту сабақ беру мен үйренуден (оқу) тұрады. Сабақ беру – оқу материалын түсіндіретін, оқушылардың оқып үйрену және білімін, біліктілігін тексеруді ұйымдастыратын, алған білімдерін қолдана білулерін басқаратын мұғалімнің іс-әрекеті. Үйрену (оқу) – мұғалімнің басшылығымен орындалатын оқушылардың сапалы іс - әрекеті, ол белгілі бір оқу материалын қабылдауын және мұғалімнің түсіндіруін тыңдауын, теория мен тәжірибе арасындағы байланыстарды ұғып алуды, қорытындылауды, мұғалімнің тапсырмасы бойынша алған білімін қолдана білуді қамтиды [3]. Бұдан оқыту әдістері сабак беру әдістері мен үйрету әдістерінен тұрады деп айтуға болады. Сабак беру және үйрету әдістері – белгілі бір математикалық білім, білік және дағды жүйесін оқушыларға беру тәсілдері деп түсінеміз. Бұл әдіске әңгімелесу, мұғалімнің түсіндіруі және дәріс, тәжірибе, жаттығу ретінде өздігінен істейтін жұмысты басқару, оқушылардың оқу құралдармен, әдебиетпен жұмыс істеуіне басшылық ету. Үйрету әдістеріне (оқып үйрену) оқу материалын танып – білу оқушылардың өз беттерімен белсенді ізденіп білім алу жолдары жатады. Оқыту үрдісінде қайсыбір әдісті қолдану үшін мұғалім сол әдісті жете меңгеруі тиіс. Ол үшін:

а) әдістің мағынасын түсіну және оны қолдана білу керек;

ә) оқыту үрдісінде әдісті қолдану барысында байқалатын жақсы және теріс жақтарын білу керек;

б) мектеп математика курсында қандай тақырыптарды осы әдіспен оқыту қолайлы екенін білу керек;

в) оқу материалын игеруде оқушыларды осы әдіспен жұмыс істеуге үйрете білу қажет.

Сонымен, оқыту әдістері – білім беру және білімді меңгеруге, азаматтық тұлға қалыптастыруға бағытталған шәкірттердің танымдылық іс-әрекеттерін және тәжірибелік қызметтерін ұйымдастыру тәсілін қамтиды.


Математиканы оқытудың жалпы әдістеріне проблемалық оқыту, эвристикалық әдіс, бағдарламалап оқыту әдістері жатады. Проблемалық оқытудың мәні-мұғалім проблеманы өзі қойып, өзі шешеді. Мұндағы басты проблема - теореманы дәлелдегенде оны қалай дәлелдеу емес, дәлелдеуді қалай іздестіру, іздестіруге оқушыларды қалай тарту мәселесі. Бұл әдістің негізгі жетістігі дербестікке, шығармашылық еңбекке, фактілерді бағалауға тәрбиелейді, проблемалық баяндау әдісін қолданғанда мұғалім-ақпараттың негізгі көзі болып табылады.

Проблемалық оқыту әдісі - математикалық білім беру үрдісінде мұғалімнің жетекшілігімен, оқушылар алдына қойылған проблемалық ситуацияны өз беттерімен шешіп, жаңа білім алу әдісі. Проблемалық оқыту кезінде мұғалім материалды баяндап, неғұрлым күрделі ұғымдарды түсіндіре отырып, сабақ үстінде ұдайы проблемалық ахуал туғызады. Мұнда фактілер мен құбылыстарды талдағанда оқушылар тиісті қорытындылар мен жалпылауларды өздігінен жасауға, ережелердің тұжырымдарын, ұғымдарын анықтамаларын беруге, ұғымдардың арасындағы байланыстарды тағайындауға және де пайда болған жаңа жағдайлармен-есептерді шығаруға бағыттау керек. Сөйтіп, проблемалық оқыту оқушылардың ойлау қызметін жандандырудың негізгі құралы-проблемалық ахуал туғызудан басталып, мына негізгі сатыларды қамтиды: а) проблеманы тұжырымдау; ә) оны шешу тәсілдерін табу, б) проблеманы шешу; в) қорытындыны тұжырымдау; г) таңдап алынған шешудің дұрыстығын көрсету.

Проблемалық ахуал деп оқушылар игерген білім мен іскерліктің және түсіндіруге қажетті фактілер мен ұғымдардың арасындағы сәйкессіздікті айтады. Бірақ проблемалық ахуалдың негізгі көзі есеп шығару болып табылады. Атап айтқанда, проблемалық ахуалдарды қамтитын есептерді шығару барысында оқушылардың ойлау қызметін шыңдауға қажетті дағдылары дамытылады. Оқу материалының проблемалы болуының қажетті шарттары мыналар: а) проблеманың түсініктілігі; б) оның танымдылығы; в) проблеманың мазмұндылығы.

А.А. Смирнова мен П.И. Зинченко «проблемалық ахуал оқушылардың есте сақтау қабілеттерін арттырады» десе, А.В. Брушлинский, Т.В. Кудрявцев

«проблемалық оқыту оқушылардың ақыл-ойын, шығармашылық қабілеттерін дамытады» - деді. Әрбір проблемалық ахуалдың өзіне тән педагогикалық сипаты болады. Оның біреуі оқушыларды ұғымдарды өздігінен меңгеріп, оның анықтамасын тұжырымдауға бағыттайды. Екіншісі, белгісіз заңдылықтарды
ашуға арналған болжамдарды көрсетеді. Үшіншісі, қойылған проблеманың практикалық және теориялық мәнін түсіндіруге түрткі болады т.с.с. Проблемалық ахуал туғызудың бір мысалын келтірейік [49]: Темір жол

құрылысын үнемі түп-түзу төсеу мүмкін емес, өйткені алынған бағытта елді мекендер, қиын асулар, өткелдер және т.б. кедергілер болуы ықтимал. Осыған орай жолдың бағытын өзгертетін жолдар салуға тура келеді. Инженерлік- техникалық есептерді шығару үшін (центрлік күшті, поездың жылдамдығын есептеу үшін) кейде орағыту радиусын өлшеу керек. Геометриялық тілде бұл проблеманы былай тұжырамдауға болады; шеңбердің берілген доғасы бойынша оның радиусын есептеу керек. Кейбір себептер бұл есепті графиктік тәсілмен шығаруға мүмкіндік бермейді. Сондықтан оны тікелей өлшеумен және есептеумен шығаруға бола ма? деген заңды сұрақ туады. Берілген доғаны керетін хордалар (BN=1/2AB сәйкес сегменттің биіктігі) тік бұрышты МВК үшбұрышының элементтері болып табылады, мұндағы МК - ізделген диаметр (1-сурет).

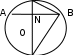
М
1-сурет

BМ катетін, оның гипотенузаға түсірілген МN проекциясының ұзындығын, гипотенузаға түсірілген NВ биіктігін өлшеу қиын емес. Осы мәліметтер бойынша МK гипотенузасын есептеу үшін, бұл кесінділердің арасындағы байланыстарды тағайындау қажет. Сабақтың мақсаты - тік бұрышты үшбұрыш элементтері арасындағы кейбір метрикалық қатынастарды қорыту. Эвристикалық әдіс - оқыту процесінде оқушылардың белсенді танымдық қызметін пәрменді ұйымдастыруға көмектеседі. Бұл әдісті қолданғанда оқушылар өздерінің алдына қойылған проблемаларды шешіп, шағын жаңалықтар ашады. Эвристикалық әдісті оқу процесінде қолдану үшін кейбір мысалдар келтірейік.

Теорема. Параллелограмның диагональдары қиылысады және қиылысу нүктесінде қақ бөлінеді.

ABCD параллелограмын сызып, диагональдарын жүргіземіз. Олардың қиылысу нүктесін О деп белгілейміз (2-сурет). Теорема шартын жазамыз.

В С
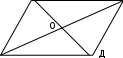А
2-сурет

Берілгені: ABCD-параллелограм, АС және BD оның диагональдары.

О- диагональдардың қиылысу нүктесі.

Дәлелдеу керек : AO=OC, BO=OD. Теорема шарты мен қорытындысын қайталаймыз.

Дәлелдеуі:

  • нені дәлелдеу керек?

  • кесінділердің теңдігі, әдетте қандай жолмен дәлелденеді?

  • қай үшбұрыштарды қарастыру қолайлы?

Осы үшбұрыштарды зерттейік. Үшбұрыштардың қандай элементтері тең?

  •  АВО=  CDO екенін көрсететін теорема қалай айтылады.?

  • Бұл үшбұрыштардың теңдігінен не шығады?

  • Дәлелденген теореманы қалай тұжырымдауға болады?

Мұнда, берілген сұрақтарға қайтарылған жауаптар тақтаға әрі дәптерге жазылады. Әңгімелесудің соңында:

  • дәлелдеу бойынша қандай сұрақтар бар?

- осы нәтижені алу үшін дәлелдеу барысын қалай өзгертуге болады?- деген сияқты сұрақтар берілуі мүмкін.

Эвристикалық әдіске тән сипат - мұғалім мен оқушылардың арасында тура әрі кері байланыстың болуы. Мұның нәтижесінде метериалды сыныптың қалай игергенін байқауға кез келген оқушының, өз қабілеті мен инициативасын көрсетуге жағдай туғызуға, селқостар мен ынтасыздарды жұмысқа тартуға мүмкіндік береді. Эвристикалық әдісті қолданғанда берілетін сұрақтар жүйесі логикалық жағынан мінсіз, материалдық мазмұны мен дәлелдеуін түгел қамтуы тиіс және қысқа, әрі анық болуы керек. Сондықтан мұғалім эвристикалық сұрақтарды алдын ала дайындап алғаны жөн. Бағдарламалап оқыту әдісі - оқу материалын арнайы бағдарлама бойынша мұғалім шағын бөліктерге бөлшектейтін және әрбір оқушының іс-

әрекетінің сипаты мен ретін анықтайтын, сондай-ақ оқытылатын материалды меңгеру барысын ұдайы бақылауға көмектесетін дидактикалық жүйені түсінеді. Бағдарламалап оқыту, әсіресе компьютер көмегімен бақылау бүгінгі таңда барлық оқу орындарында кеңінен пайдаланылады. Қазіргі уақытта компьютердің көмегімен жоғары оқу орындарында студенттердің білімдерін тексереді және емтихандар өткізіледі. Кейінгі жылдары оқу процесін басқаруға арналған компьютерлер дүниеге келді. Қазіргі таңда компьютерлік техниканы жаппай меңгеру, бұл техниканы оқып үйрену объектісі ретінде қараумен бірге, оқыту құралы ретінде де қарастыруға жол ашты. Бағдарламалап оқытудың ерекшеліктері мынадай: 1) бағдарламалап оқыту әдісі оқытуды жекелеп жүргізу қағидасына негізделген. Оқу материалын оқушылардың өздігінен меңгерулері жүзеге асады. Оқушылар оқу құралы бойынша өз бетімен оқып үйрену үшін бар қабілетін, ақыл-ойын жұмсайды. Оқу құралында оқушыларға қажетті бар теориялық материал, оқушы ойланып шешімін табатын тапсырма, сұрақтар келтіріледі; 2) оқу материалы оқып үйренуге ыңғайлы бірнеше шағын

Смотрите также файлы