Файл: Алпысов А.. Математиканы оыту дістемесі оу ралы Павлодар, 2012.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 1751
Скачиваний: 140
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. Математиканы оқыту әдістемесі пәні
2. Математиканы оқытудың мақсаттары мен мазмұны
Математиканы оқытудың қағидалары
Математиканы оқытудың әдістері
5. Математикалық ұғымдар, сөйлемдер және оларды үйренудің әдістемесі
6. Математиканы есептер арқылы оқыту әдістемесі
Математикадан сыныптан тыс жұмыстар, оны өткізу әдістері
9. Педагогикалық практика туралы
түрінде қойылуын қысқаша әңгімелеудің рөлі зор.
Факультативтік курстың маңыздылығын арттыру жолдарының бірі – практикалық жұмыстар орындау. Сабақтың бұл түрі оқу процесін білімді іс жүзінде қолданумен ұштастыруға жол ашады. Мұнда мұғалім ең алдымен оқушыларды практикалық жұмыстың мақсатымен, жұмыс істеу тәртібімен таныстыруы, қажетті нұсқаулар беруі тиіс. Берілетін практикалық тапсырмаларды жеке ерекшеліктеріне қарай берген дұрыс, ал жұмыс нәтижесін күллі топтың қызметі ретінде бағалау керек. Мәселен,
«Көпжақтар» тақырыбы бойынша практикалық жұмыс жүргізгенде көпжақтардың эскизін, олардың жазбалары мен модельдерін салу керек. Дұрыс көпжақтардың модельдерін әр оқушы жеке, ал күрделі көпжақтарды 2-3 оқушы бірлесіп орындағаны дұрыс. Мұның өзі ұжымдық еңбекке баулиды. Факультативтік курстың материалдарын терең игеру жолдарының бірі – күрделі есептерді эвристикалық жолмен шығару. Алайда, есептерді оқушылардың ынта – ықыласына сай іріктеп алса, оның тиімділігі арта
түспек. Алдымен даярлық есептер оқушылардың өздігінен шығармашылық қызмет ету қабілетін дамытатындай, проблемалық ахуал ретінде берілуі тиіс.
Математиканың бірегейлік сипаты бұл ғылымның өзінің ішкі болмысынан туған; шынында да математика – бүкіл дәл жаратылыстану ғылымының негізі. Ал математиканың осынша биік мәртебелі ролін кемел орындауы үшін, келешек ғасырда оның жолына данышпан шеберлер мен көптеген ізгі талапты жастар келе беруінтілейік.
Гильберт Д.
9. Педагогикалық практика туралы
-
Педагогикалық практиканың мақсаты және мазмұны туралы.
-
Студент – практиканттарға қысқашанұсқаулар. -
Сабақты талдаусхемасы.
-
Педагогикалық практика студенттің кәсіби біліктілігін жетілдіруге мүмкіндік беретін маңызды сала. Педагогикалық практика мемлекеттік жалпыға міндетті білім беру стандартына сәйкес көрсетіледі және студенттің жеке оқу жоспарына енеді.
Педагогикалық практиканың мақсаты: студенттерге оқушыларды оқыту және тәрбиелеуде мұғалімге қажетті білік пен дағдыны қалыптастыру. Педагогикалық практика кезінде студент-практиканттар әдіскердің, психологтың және педагогтың көмегімен төмендегідей қабілеттерге ие
болады:
-
педагогикадан, психологиядан, математиканы оқыту әдістемесінен және арнайы курстардан алған теориялық білімдерін практикада қолданады; -
мектепте өз бетімен оқу-тәрбие жұмысын жоспарлайды және жүргізеді. Ата-аналармен жұмыс жүргізеді және оқушылардың тәрбие жұмысында кейбір проблемаларды шешуде белсенділік көрсетеді; -
мектеп ұжымының өміріне араласып, сыныппен және ата- аналармен белсене жұмыс істейді; -
мектеп оқытушыларының жинаған тәжірибесін бақылайды, талдайды және қорытындылайды.
Педагогикалық практика студенттерді болашақ мамандыққа дайындауда алатын орны зор, яғни студентер: а) институтта алған білімдерін бекітеді және тереңдетеді; ә) педагогикалық мамандыққа сүйіспеншілігі орнығады; б) педагогика саласында ғылыми-зерттеу жұмысына қызығушылығы туындайды; в) курстық және дипломдық жұмыстарға материалдар жинайды, мектепте эксперимент жүргізеді.
Педагогикалық практиканы өту кезінде студенттер мектеп ұжымының жұмыстарының барлық салаларына қатысты тапсырмалар орындайды. Мұндай тапсырмаларды орындау студенттердің мектеп жұмысымен терең танысуларына жағдай жасайды, теориялық білімдерін жетілдіреді және педагогика ғылымдар саласынан, оның ішінде математиканың әдістемесінен ғылыми-зерттеу жұмысын жүргізуге ынталандырады.
Студент-практиканттар сабақтың төмендегідей түрлерін жүргізіп үйренулері керек:
а) оқушыларды жаңа материалмен таныстыру сабағы;
ә) оқушылардың білім, білік және дағдыларын бекіту сабағы; б) оқушылардың білім, білік және дағдыларын тексеру сабағы; в) жаттығу сабағы;
г) аралас сабақтар және т.б.
-
Студент – практиканттарға қысқаша нұсқаулар:
-
Мұғалім сынып бөлмесіне оқушылар орындарына отырғаннан кейін кіреді. -
Сынып бөлмесінің тазалығы және сыныптың сабаққа дайындығы тексеріледі. -
Сыныпта жұмыс жүйесі жасалғаннан кейін оқушыларға сабақ жоспары айтылады. Үй тапсырмасы тексеріледі. Жаңа сабаққа дайындау мақсатында жаттығулар шығарылады. -
Жаңа материалды түсіндіргенде өткен тақырыппен логикалық байланыс жасалады. -
Оқушылардың сабаққа қызығушылықтарын дамыту үшін проблемалық сұрақтар, тарих элементтері, өз бетімен жұмыс т.б. қолданылады. -
Үнемі оқушылардың шығармашылық қабілеттерін дамытуға көңіл бөлінеді. Есеп шығарғанда, оны шешудің тиімді жолын іздеуге дағдыланады. -
Сабақты күнделікті қорытындылаудың және бағалаудың маңызы зор. Оқушылардың келешектегі белсенділігі олардың білімдерін әділ бағалау мен үйге тапсырманы орындауға бағыттау жұмыстарына байланысты.
-
Психология-педагогикалық теорияның көмегімен әр түрлі негізде құрылған сабақты талдаудың көптеген схемасы белгілі. Сабақты талдау схемасын таңдап алу үшін оқушылардың білімділік сапасының қазіргі өлшемдерін білу, оқыту мен тәрбиелеудегі сәттерді анықтаудағы және оны жеңудегі ой-ізденістік қызмет тәсілдерін игеру, педагогикалық қызметтің мәдени және адамгершілік мағынасын құру, оқытылатын білімнің мазмұнын таңдау және қайта құра білу, оқушылардың өз бетінше ұйымдастыруының негізгі құралдарын модельдеу және құру жеткілікті.
Сабақты талдау схемасы:
-
Мектеп, сынып, сабақ, студент-практиканттың не мұғалімнің аты,
тегі.
-
Сабақтың тақырыбы, сабақтың оқу-тәрбие мақсаттары, сабақ
түсіндірудің жүйелілігі, қойылған мақсатқа жетуде оқушылар ұжымын ұйымдастырудың дұрыстығы.
-
Сабақты ұйымдастырудың бастапқы моменті:
а) мұғалімнің сабаққа дайындығы (сабақ конспектісі және толық сабақ жоспары, көрнекі құрал-жабдықтар және т.б. бар болуы);
ә) оқушылардың сабаққа дайындығы (кезекшілік, оқушылардың сабаққа қажетті дәптерлері, оқулық, оқу-құралдары және т.б. болуы);
б) сынып бөлмесінің сабаққа дайындығы (тазалық, тақта, бор және т.б.).
-
Сабақтың ұйымдастыру құрылымы:
а) сабаққа оқушыларды түгел жұмылдыру;
ә) сабақтың оқу материалының мазмұнына сәйкестігі; б) сабақты жүргізу жүйесі;
в) мұғалімнің сыныппен қарым-қатынасы;
г) сабақ уақытындағы оқушылардың белсенділігі.
-
Сабақтағы оқу материалының мазмұнын талдау: а) оқу материалының ғылымилығы;
ә) оқушылардың білім деңгейі бағдарламаға сәйкестігі; б) практикалық және теориялық материалдың сәйкестігі;
в) оқу материалдың жүйелігі;
г) сабақ материалының тәрбие мақсатына сәйкестігі; д) өмірмен және практикамен байланыс.
-
Сабаққа қойылатын жалпы педагогикалық және дидактикалық талаптардың орындалуы. -
Мұғалімнің іс-әрекеті. -
Сабақтағы оқушылардың іс-әрекеті. -
Сабақты бағалау:
а) сабақ жоспарының орындалуы; ә) сабақтың мақсатына жетуі;б) сабақтың міндетінің орындалуы; в) ерекше үлгі аларлық мәселелер; г) сабақты қайталап өткізгенде қандай өзгерістер енгізуге болады?
-
Қорытынды жасау және баға қою.
Дәлелдемелерінің кең мағыналылығы жағынан геометрия сияқты ғылымдар басқа ғылымдардан жоғарыбағаланады.
Әл-Фараби
10. Геометрияны оқыту әдістемесі
-
Планиметрия курсын үйрену әдістемесі.
-
Геометрия есептерін шешудіңәдістері.
-
Стереометрия курсын үйренуәдістемесі.
-
Геометрияны оқытуда есептерді шеше білу дағдысын қалыптастыру және оны жалпы түрде дамыту аса маңызды мәселелердің бірі болып табылады. Геометриялық есептерді шешу туралы жалпы білік- дағдылар әдетте көптеген есептерді шешу арқылы қалыптасады. Олай болса, студент пен оқытушының не мұғалім мен оқушының жүйелі түрде ұзақ уақыт еңбектенуіне тура келеді. Шешілу жолы беймәлім, әр түрлі теориялық
фактілерді байланыстыруды қажет ететін, студенттер шығара алмайтын жаңа есептер де жиі кездеседі. Сондықтан студенттерді кез келген геометриялық есепті шешудің жалпы тәсілдерімен қаруландыру керек. Бұл талап математикалық есептерді шешу практикумының бағдарламасында да айтылған. Практикум белгілі бір есептердің түрлерін және оларды шешудің тәсілдерін таныстыруға бағытталып қана қоймай, қайта дәлелдеудің барынша жалпы әдістерін ойлауды меңгерту болып табылады. Оқытушы студентке әрбір есепті шығартқанда, оның шешімін әдістемелік талаптарға сай іздеуге, соңында мақсатқа сай дұрыс шешімді табуға жәрдемдесетіндей талдау тәсілдері мен болашақ мұғалімдерге қажетті білім-білік дағдыларын қалыптастыруға ұмтылады. Теориялық және әдістемелік білім мен әдіс- тәсілдерінсіз кез-келген әдістемелік есепті шешуге бола бермейді. Практикадан байқалатындай, көбінесе геометрия есептері әр түрлі тәсілдермен логикалық тұрғыда көбірек ойлануды қажетсінеді. Геометрия есептерін шешудің кезеңдерін білу оқушылар мен студенттерде қалыптастырылуға тиісті аса маңызды дағдылардың бірі. Есептерді шешу процесі келесі кезеңдерден тұрады.
-
Есептің шартын түсіну: а) есепті талдау; б) есеп шартын схема түрінде жазу. Есепті талдағанда оның шарты қандай, онда қандай талап қойылған (не берілген, не белгілі, есеп шарты неден тұрады?) екені анықталады. Есеп шартын схема түрінде жазғанда оның сызбасы қоса қарастырылады, осы талдаудың нәтижесінде есеп шартындағы ең керекті, таныс элементтер ескеріліп, олар қысқаша жазылады. Есепті талдау мен оның сызбасын және шартын схема түрінде қысқаша жазу — есепті шешу үшін жоспар іздеудің негізгі құралы болып табылады. Есепті талдай келе осы есепке қандай мөлшерде теориялық білімнің қажет болатындығы анықталады.
-
Есеп шешімін іздеу — есепті шешудің тәсілін іздеу, бұл бүкіл процестің негізгі бөлігі болып табылады. Бұл кезеңде ең алдымен берілген есептің түрі (типі), яғни оның дәлелдеуге, есептеуге не геометриялық түрлендіруге берілгені анықталады, осыған орай есепті шешу тәсілі ізделеді. Есеп шартында берілген элементтер мен іздеуге, анықталуға тиісті белгісіздер арасындағы байланыс ізделеді. Есеп шешімін іздеуде бір-бірімен тығыз байланысты мынадай екі жақты мәселені анықтайды: а) белгілі теориялық білімді шешілуге тиісті есеп шартына сай түрлендіру; б) есеп шартын белгілі теориялық фактілерге сәйкес және оларға байланысты түрлендіру. Бұл арада теориялық білім деп отырғанымыз математикалық ұғымдар мен олардың анықтамалары, теоремалар және математикадағы негізгі әдістер (координаттар әдісі, векторлық әдіс, геометриялық түрлендірулер мен теңдеулер құру әдісі және т.б.). Есептердің түрі мен құрылысына қарай оларды кластарға жіктеп талдау мен шешу әдістерін таңдап алады. Әсіресе, бірнеше теориялық материалдарды біріктіретін, әрі күрделі, әрі көптеген есептерді шешуге теориялық әдістемелік негіз болатын тірек есептерін талдау кезінде белгілі бір гипотеза ұсынылады және оның іске асырылуы тексеріледі. Есеп шешімін іздеу үшін гипотеза ұсына отырып,
осы есепке нақтылы қандай теориялық материал керек болатынын анықтаймыз. Теориялық білімді негіздеуші әдісті таңдап, гипотезаны тексереміз. Егер есепті талдағанда бұрыннан таныс элементті байқасақ, не ол шешілуі таныс есепке ұқсас болса, онда есепті шешу үшін белгілі әдісті қолдану мүмкіндігі туралы ой, не есепті шешу жоспары пайда болады. Егер есептің таныс емес түрін шығаруға тура келсе, онда одан бұрыннан таныс есептердің кемінде бір элементін іздейміз немесе берілген есеп шартын бұрын шешілген есептегі таныс бір элемент табылатынын талдаймыз.
-
Жоспарды іске асыру. Бұл арада шешу идеясы табылып, есеп шешіледі.
-
Шешілген есепті талқылау: а) есеп шешімін тексеру; б) есепті зерттеу; в) есеп шешімін әр түрлі параметрлер мен байланыстар бойынша талдау.
Есептің шешілуінің және оған қолданылған әдістер мен теориялық негіздеулердің дұрыс екенін, ол шешім есеп шартының барлық талаптарын қанағаттандыратынын білу үшін оны тексеру керек. Есепті зерттеу келесі мәселелерді анықтауы керек: қандай шарт орындалғанда есептің шешімі бар; қандай шарт орындалғанда есептің жалпы шешімі жоқ болады?
Есептің шешімін талдау мынадай мәселелерге жауап береді. Есепті шешудің бұдан басқа ең тиімді жолы жоқ па? Есепті жалпылауға бола ма? Осы есептен қандай қорытындылар жасауға болады? Есепті шешу процесінің құрылымы ең алдымен есептің сипатына, есеп шығарушының қандай біліммен, білікпен, дағдымен қаруланғанына тікелей байланысты.
-
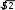 мысал. Тікбұрышты үшбұрыштың катеттеріне жүргізілген
мысал. Тікбұрышты үшбұрыштың катеттеріне жүргізілген
медианалары
см және
см. Оның гипотенузасын табу керек (8-сурет).

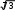 А
А
Е
С В
F
8-сурет
Шешуі. ВС мен AC катеттерін сәйкес х пен у ар-ылы белгілейік.
ВСЕ, ACF — тікбұрышты үшбүрыштар болғандықтан,
ВС 2 BE 2 EC 2
және
CF2
AF 2
-
AC
2 , яғни x
2
2 y
73
4
және
x 52 y2
2
4
. Бұл тендеулер жүйесін
шешіп, х пен у-ті табамыз:
 73 0,25y2 4 52 4y2 ,
73 0,25y2 4 52 4y2 ,
y2 36 ;
y 6cм ,
х 8см;
АВ
10см .
-
мысал. ABC үшбұрышында АВ=26см, BC=30см, АС=28см. В төбесінен ВН биіктігі мен BD биссектрисасы жүргізілген. BHD үшбұрышының ауданын табу керек.
 Шешуі. ABC үшбұрышының ауданын екі әдіспен өрнектейік:
Шешуі. ABC үшбұрышының ауданын екі әдіспен өрнектейік:
SAВС
0,5АС ВН
0,5 28 h 14h ; екінші жағынан
S АВС
336см2 .
Демек, 14h=336, h=24 см. Енді CD=x деп алып, ABC үшбұрышының ішкі бұрышы биссектрисасының қасиетін пайдаланайық: ВС:АВ=CD:DA, 30:26=x:(28-x), х=СD=15см; AD=28-15=13см. ВСН : СН 2 ВС 2 ВН 2 324,
CH=18 см, DH=CH-CD=18-15=3см, S=0,5
DH ВН
36см2 .
-
мысал. Медианалары
mb 9см ,
ma 12см ,
mc 25см
болатын
үшбұрыштың ауданын есептеу керек (9-сурет).
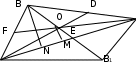 С
С
А
-
сурет
Шешуі.
ABC : mb BE 9см ,
ma AD 12см .
mc CF 15см. Берілген
элементтер мен іздеген элементтің арасындағы байланысты анықтайық (О — медианалардың қиылысу нүктесі).
AOC : AО 2 m 2 12 8см , OC 2 m
10см , OE 1 m
3см
3 a3
3 с 2 b
ОЕ медианасын екі еселеп, АОС үшбұрышын AOCB1
параллелограмына дейін толықтырайық. Сонда AC 2 OB2 2(AO2 OC2 ) ;
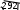 AC . Осы сияқты OD медиананы екі еселеп, ВОС үшбүрышын
AC . Осы сияқты OD медиананы екі еселеп, ВОС үшбүрышын
параллелограмға толықтырсақ:
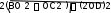
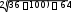
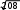 BC .
BC .
Осылай қарастырып, АВ=10см екенін аламыз. Енді Герон
ABC
формуласымен ауданды есептесек, S 72см2 .
Осы есепті басқа әдіспен шешейік.
AOC мен
ABC -ның табандары тең
болғандықтан, S
1 S
Шынында да,
OME BNE ,
OM OE , ал
OE 1
AOC
3 AOC
BN BE
BE 3
болғандықтан,
OM 1 . Сондықтан
BN 3
SAOC SABC
OM
BN
1 ,
3
SAOC
1 S
3
ABC
Енді
AOCB1
параллелограмынан:
1
SAOC SOCB ;
OC 2 EC 2 15 10 , CB AO 2 m 8, OB 2OE 2 1 9 6 ,
AOC
ABC
3 3 1 3 a 1 3
p 12 ,
S 24см2 ,
S 72см2
-
Геометрия есептерін шешудің әдістеріне: а) геометриялық;
б) алгебралық; в) комбинациялық деп аталатын негізгі әдістер жатады.
Есептерді геометриялық әдіспен шешкенде логикалық ойлаудың жәрдемімен белгілі теоремалар арқылы тұжырымдауды қажетсінетін сөйлемдерді дәлелдейміз. Ал есептерді алгебралық әдіспен шешкенде ізделінген шаманы табу, не тұжырымдауға тиісті сөйлемді дәлелдеу тікелей есептеу жолымен немесе теңдеулер мен олардың жүйелерін құру арқылы іске асады. Тікелей есептеу әдісінің мәні мынада: есептің берілгендері мен белгісіздерінің жан-жақты байланыстарынан аралық қосымша белгісіз шамалар тізбегі құрылады, тізбекке қатысытын әрбір белгісіз шама анықталады немесе іздеген шама белгілі шамалар арқылы өрнектеледі.
-
- мысал. Теңбүйірлі ABC үшбұрышының табаны AC, төбесіндегі В бұрышы сүйір, С бұрышының биссектрисасы CD кесіндісі болсын. D нүктесі арқылы CD биссектрисасына перпендикуляр түзу жүргізілген. Бұл түзу үшбұрыштың AC табанымен немесе оның созындысымен Е нүктесінде қиылысады. AD =0,5ЕС болатынын дәлелдеу керек (10-сурет).
 В
В
F
D
Е А K С
-
сурет
Есеп геометриялық әдіспен тікелей шешіледі. CD кесіндісі — EFC үшбұрышының әрі биіктігі, әрі биссектриссасы. D нүктесін ВС қабырғасымен (CD EF және CD — С бұрышының биссектриссасы) қиылысқанша созсақ, EFC теңбүйірлі үшбұрышы шығады. Есептің шарты бойынша CD EF. Ендеше ED = DF. D нүктесінен ВС-ға параллель түзу жүргізсек, ол AC табанымен К нүктесінде қиылысады. Бұл DK кесіндісі EDC үшбұрышының медианасы бола алады. ЕК:КС = ED:DF = 1, бұлардан DK = 0,5ЕС, сондықтан AD = DK= 0,5 EC.
-
-мысал.Теңбүйірлі трапецияға іштей дөңгелек сызылған. Трапеция
ауданының дөңгелек ауданына қатынасы
-ге тең. Трапецияның үлкен
8
табанындағы сүйір бүрышын табу керек (11-сурет). ABCD — теңбүйірлі
трапециясы берілген,
Sдон : STP : 8 .
Бірінші тәсіл. Есептің мазмұнынан оны синтез әдісімен немесе алгебралық әдіспен шешуге болатынын байқаймыз. Синтез әдісі бойынша
берілгендерге сүйеніп дөңгелектің радиусын табуға болады. Дөңгелектің радиусын г, трапецияның табан қабырғалары ұзындықтарын a, b деп қосымша белгісіздер ендіреміз. Есеп шарты бойынша
r 2
0,5(a b) 2r
, 8
a b 8r,
r a b .
8
Екінші жағынан шеңберді сырттай сызылған төртбұрыштың қасиеті бойынша AD+BC=AB+DC теңдігін жаза аламыз. Бұдан 2AD=a+b,
AD=0,5(a+b). Тікбұрышты AED үшбұрышынан
sin A DE
AD
4r a b
; бұл
теңдікке r-дің мәнін қойып ықшамдасақ, sin A = 0,5 шығады. Сонымен,
A .
6
 A B
A B
E
-
сурет
Бұл есепте жоғарыда айтылған тірек элементін және қосымша белгісіздер енгізу, теңдеу құру, қосымша белгісіздерді ығыстыру процестерінің барлығы орындалады.
Екінші тәcіл. 11-суреттен AD=BC теңдігін ескеріп, бір нүктеден шеңберге жүргізілген екі жанама тең болатынын пайдалансақ,
AN a ,
2
NN b,
2
sin A DE
AD
2r
AN ND
4r .
a b
r-дің 1-тәсілдегі мәнін орнына қойсақ, sinA = 0,5, бұдан
A .
6
Теңдеулер құру арқылы шешілетін есептерді қарастыралық.
6-мысал. Тікбұрышты үшбұрыштың гипотенузасы с-ға тең, үшбұрыштың бір сүйір бұрышынан катеттерінің біріне ұзындығы m-ге тең медиана жүргізілген. Осы үшбұрыш катеттерінің ұзындықтарын табу керек (12-сурет).
 В
В
D
С А
12-сурет
Есепті теңдеу құру әдісімен (алгебралық әдіспен) шешу үшін АС=x, BC=y деп белгілейік. Тікбұрышты үшбұрыштардан Пифагор теоремасы
бойынша:
АС 2 ВС 2 AB 2 ,
АС 2 СD2 AD2
немесе
x2 y2 c2 ,
x2
(0,5y)2
m2 . Бұл жүйенің шешімі
BC 2
, AC .
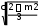
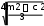 Математикалық есептердің көбінде қосымша белгісіздер енгізу әдісі қолданылады. Бұл есептердің берілген элементтері мен қажетті теориялық материалдарды байланыстыруға септігін тигізеді. Есепті шешу барысында осы қосымша белгісіздер ығысады.
Математикалық есептердің көбінде қосымша белгісіздер енгізу әдісі қолданылады. Бұл есептердің берілген элементтері мен қажетті теориялық материалдарды байланыстыруға септігін тигізеді. Есепті шешу барысында осы қосымша белгісіздер ығысады.
7-мысал. Ромб биіктігі оның қабырғасын m және n бөліктерге бөледі.
Ромб диагоналдарының ұзындықтарын табу керек (13-сурет).
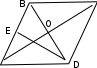 С
С
А
13-сурет
-
тәсіл. Теңдеулер құруға қажетті белгісіздер енгізелік. Ол үшін АС=x,
BD=y деп белгілейміз. Сонда
АВ AE EB m n.
Бұл қосымша элементті
есеп шартындағы белгілі және белгісіз шамалар арқылы өрнектейміз. ЕD h
десек,
h2 y2 n2
және
h2 (m n)2 m2.
h2 -тың мәндерін теңестірсек,
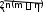 у2 n2 (m n)2 m2, х-ті табамыз:
у2 n2 (m n)2 m2, х-ті табамыз:
y 2 2mn 2n2
немесе
y . АОВ үшбұрышынан
 АО2 AB2 OB2 (m n)2 (0,5
АО2 AB2 OB2 (m n)2 (0,5
 AC x 2AO
AC x 2AO
2n(m n))2 ,
.

 Сонда жауабы: 2n(m n), .
Сонда жауабы: 2n(m n), .
-
тәсіл. Аудандарды пайдалану әдісі бойынша
0,5d1d2
шамасын

 қосымша элементтер арқылы табылатын ауданға теңестіреміз, яғни
қосымша элементтер арқылы табылатын ауданға теңестіреміз, яғни
0,5d1d2 (m n)
2n(m n) , мұндағы
h 2n(m n) . АОВ үшбұрышынан
(0,5d )2 (0,5d )2 (m n)2 немесе d 2 d 2 4(m n)2 . Бірінші теңдіктің екі
1 2 1 2

 жағында 4-ке көбейтіп екінші теңдікке қоссақ, онда
жағында 4-ке көбейтіп екінші теңдікке қоссақ, онда
1 2
(d d )2 4(m n)
4(m n)2 4(m n)(
m n).
Бірінші теңдіктен d1 -ді тапсақ және оны соңғы теңдікке қойсақ,
түрлендіргеннен кейін
d болады. Енді d 2 4(m n)2 d2
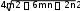
 2 1 1
2 1 1
теңдігіне
d 2 -нің табылған мәнін қойсақ,
d1 екені шығады. Егер
берілген есепте кейбір шамалардың (ұзындықтардың немесе аудандардың) қатынастарын табу қажет болса, дербес жағдайда белгілі бір бұрышты есептеу қажет болса, ондай есептер көмекші параметр енгізу деп аталатын тәсілмен шешіледі. Бұл тәсіл бойынша есепті шешу үшін сызықтық
элементтердің біреуін белгілі деп алып, іздеп отырған шаманы сол арқылы өрнектейді де олардың қатынастарын құрады.
-
Мектеп оқушыларының кеңістікті қабылдап, оны көз алдына елестете алуы стереометрияны оқытудың негізгі мәселелерінің бірі болып саналады. Осы айтылған мақсатты іс жүзіне асыруда кеңістіктегі салуға берілген есептерді шешудің зор мәні бар. Жазықтықтағы геометриялық салулар теориясы жеткілікті түрде талқыланып қарастырылады, ал стереометрияның әдістемелік мәселелеріне әлі де толық көңіл бөлінбей келеді. Геометриялық салулар теориясы – салуды негіздеу, есептерді кластарға жіктеу, есеп шешу әдістері, белгілі бір класқа жататын есептерді шешу критериі, салу есептерін шешкенде барынша жай әдістерді тиімді қолдану сияқты мәселелерді қарастырады.
Кеңістіктегі салу есептерін кластарға жіктеу туралы әр түрлі көзқарастар мен тәсілдер бар. А.Н. Чалов кеңістіктегі салу есептерін геометриялық салуды орындау тәсілдері бойынша келесі топтарға бөледі: 1) елестету арқылы шешілетін есептер; 2) проекциялық сызбамен шешілетін есептер; 3) модельмен шешілетін есептер. Салуға берілген стереометрия есептерін позициялық және метрикалық деп екі топқа бөлетіндер де бар. Негізгі элементтерінің қиылысуын ғана іздейтін, соны салумен аяқталатын есептер позициялық әдіспен шешілетін есептерге жатады. Кесінді салу, белгілі бір шамасы бар бұрышты салу, перпендикуляр тұрғызу, биссектриса жүргізу және т.б. белгілі шарттарды қанағаттандыратын фигура салу талабы қойылатын есептер метиркалық есептерге жатады. Мысалы, В.А. Гусев, В.Н. Литвиненко, А.Г. Мордкович өздерінің құрастырған «Математикалық есептер шешу практикумында» кеңістіктегі салуға берілген есептерді мынадай әдістер бойынша топтарға бөледі: 1) кеңістіктегі қарапайым салулар; 2) нүктелердің геометриялық орындары; 3) кейбір нүктелердің геометриялық орындары мен түзулерді пайдалану; 4) кескіндеу арқылы салу.
Салуға берілген стереометрия есептері талдау, салу, дәлелдеу және
зерттеу сияқты төрт кезеңнен тұрады.
Талдау – бір бүтінді, құрамды бөліктерге жіктейтін, әр бөлікті жеке қарастыратын зерттеу әдісі. Ол салу есебін шешудің жоспарын табуға мүмкіндік тудырады. Талдау – есеп шешудің барынша маңызды кезеңі. Есепке дұрыс жүргізілген талдау – есепті шешу жоспарын дұрыс құрастырудың кепілі. Салу есебіне талдау жасағанда сызба басты рөл атқарады. Сонда есеп шартын, сызбадағы элементтердің өзара орналасуына барынша басынан аяғына дейін талдау жасалады, есеп шартында берілгендер мен іздеген элементтер арасында байланыс орнатылады. Есептің салу кезеңінде салу есебіне қолданылатын аксиомаларды, теоремаларды, қосымша қарапайым салуларды дәл көрсету керек. Дәлелдеу кезеңі есеп шешімінің дұрыстығына күдік туғанда қажет болады. Салу есебін зерттеу кезеңінің өзіндік маңызды ерекшелігі бар. Ол қандай шарттар орындалғанда есептің шешуі бар болады және неше шешімі бар деген сұрақтарға жауап береді. Сонымен бірге зерттеу кезеңі кеңістік елесті дамытуға мүмкіндік туғызады.
Салуға берілген алғашқы есепті шығарғанның өзінде есепті шешудің кезеңдерін (талдау, салу, дәлелдеу, зерттеу) дәл анықтап бөлу керек.
Кеңістіктегі салуға берілген есептерді шешудің негізгі әдістері:
аксиоматикалық әдіс, проективтік әдіс, геометриялық орындар әдісі.
Аксиоматикалық әдістің негізгі мәні есепті шешу кезінде салудың өзі орындалмайды, салуға берілген есеп элементар салуларға келтіріледі, кейін бұлардың бәрін бірге қарастыруға болатындай түрдегі барлық жай амалдар қарастырылады. Салу есебінде көрсетілген амалдар кейде аксиомалар деп, ал есепті шешу әдісі аксиоматикалық әдіс деп аталады. Себебі есепке қолданылатын барлық амалдар елестеу арқылы формальді түрде жүргізіледі де логикалық түрде негізделеді, мұндай әдіс формальді-логикалық әдіс деп те аталады. Әдетте логикалық ой тұжырымдары сызба арқылы жүрізіледі. Бұл есеп шешімін барынша жеңілдетеді: ойды іске қосады, көптеген геометриялық элементтер мен олардың жиынын есте сақтап қалуға, кеңістік жөнінде дұрыс түсінік орнығып қалыптасуына мүмкіндік берді. Аксиоматикалық әдіс оқушылар санасында кеңістік туралы түсініктің, логикалық ойлаудың дамуына барынша терең және берік теориялық білім алуға, әсіресе белгілі бір салуларға түсінік беретін стереометрияның алғашқы теоремаларын үйренуге мүмкіндік туғызады. Есептер шешу кезінде алдымен көрнекі құралдар – жазықтықтар моделі (нұсқасы), нүктелер мен түзулерді мақсатты түрде қолдану пайдасы зор. Осындай әдістер көмегімен салудың талаптары айқын түрде көрсетіледі, бұдан соң логикалық түрде негіздеу және логикалық негізде салынған кескінді салу дәлелденеді. Модельдеу есеп шешімін көрнекі түрде талдау жасауға, талдауды ықшамдауға мүмкіндік береді.
Проективтік әдіс (проекциялық сызбада салу есебін шешу әдісі). Егер ерекше проекциялау ережесі бойынша геометриялық денелердің кескінін пайдалануға мүмкіндік болса, онда ол есепті сызбалық құралдың көмегімен барлық салу жұмысын орындауға болады. Мұндай кескін геометриялық денені бір жазықтыққа проекциялау жолы мен алынады және проекциялық сызба деп аталады, ал есепті шешу әдісін «проекциялық сызбада салынатын есеп» деп атайды.
Кеңістіктегі салу есептерін шешуге барынша ынғайлы әдіс – еркімізше алынатын параллель проекциялау. Ол сызбаның көрнекілігімен, оны салудың өте жай қарапайым болатынымен сипатталады. Проекциялық сызба арқылы шешілетін салу есептері төрт кезеңнен тұрады. Бірақ барлық кезеңдерді әр есепте түгел іске асыру талабы қойылмайды.
Геометриялық орындар әдісі. Кеңістікте элементтердің геометриялық орындарын табуға берілген кез келген есепті салу есебі ретінде тұжырымдауға болады. Кеңістіктегі геометриялық орындар әдісімен салуға берілген есептерді шешудің мәні төмендегі мәселелер арқылы сипатталады. Әуелі есептегі берілген шарттардың біреуінен басқасын ескерусіз қалдыра тұрамыз. Өзіміз әдейі таңдап алып қалаған бір ғана шартты қанағаттандыратын нүктелер жиынын қарастырамыз. Бұдан әрі есептің екінші шартын қанағаттандыратын нүктелер жиыны қарастырылады және
т.с.с. Біз қарастырған барлық жиындардың қиылысуы есептің шешімі болады. Кеңістіктегі салу есептерін шешудің тек төрт әдісін қарастырдық. Кеңістікте салуға берілген есептерді шешудің басқа да әдістері бар. Есептер шешудің бір немесе басқа әдісін таңдап алу шешілуге тиісті есептің сипатына, есеп шығарушының дайындық дәрежесіне, т.б. байланысты. Күрделі есептерді шешу кезінде көбінесе бір мезгілде бірнеше әдіс қатарынан қолданылады.
Кеңістіктегі салуға берілген есептерді шешуге мысалдар қарастырайық.
-
мысал. Берілген а және b түзулеріне паралелль, берілген А нүктесінен өтетін жазықтық жүргізу керек.
Талдау. Іздеген жазықтық а түзуіне паралелль а1
түзуі арқылы өтуі
керек. Дәл осы сияқты іздеген жазықтық b түзуіне паралелль b1
түзуі арқылы
өтуі керек. а1
және b1
түзулері А нүктесі арқылы өтуі керек.
Салу. 1. А нүктесі және а түзуі арқылы жазықтығын жүргіземіз. 2.
жазықтығында А нүктесі арқылы а түзуіне паралелль а1
түзуін
жүргіземіз. 3. А нүктесі және b түзуі арқылы жазықтығын жүргіземіз. 4.
жазықтығында А нүктесі арқылы b түзуіне паралелль b1 түзуін жүргіземіз. 5.
а1 және b1
түзулерінен бір-бірден М және N нүктелерін таңдап аламыз. 6. А,
М, N нүктелері арқылы іздеген а жазықтығын жүргіземіз.
Дәлелдеу. 1. Салуымыз бойынша
а1 а
және
а1 . яғни,
а
. 2.
b1 b -бұл салуымыз бойынша және
b1 . Демек,
b
. 3.
A a1
және
A b1 .
сонда, A.
Зерттеу. А нүктесінің а немесе b түзулерінде жатуына тәуелсіз есептің әрқашан шешімі болады. Егер а мен b түзулері паралелль болмаса,
онда есептің бір ғана шешімі бар болады. Ал көп шешуі бар болады.
а b
болса, онда есептің сансыз
-
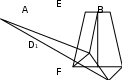
мысал. Барлық төрт қабырғасы және қарама-қарсы екі қабырғасының орталарын қосатын кесінді берілген жағдайда ABCD төртбұрышын салу керек (14-сурет).
 D С
D С
C1
14-сурет
Шешуі. ABCD — ізделген тертбұрыш, EF — АВ және DC қабырғаларының орталарын қосатын кесінді болсын. AD қабырғасын
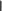
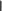 параллель жылжытып
параллель жылжытып
ED1
және ВС қабырғасын параллель жылжытып
EC1
жағдайына келтіреміз, сонда
DD1 AE ,
DD1
AE ; CC1 BE ,
CC1
BE , DF CF —
бұлар шарт бойынша, демек,
DD1 F FC1C
(екі қабырғасы және олардың
арасындағы бұрышы бойынша тең). Бұл үшбұрыштардың теңдігінен
DFD1 CFC1
шығады. Демек,
D1 , F және
C1 — нүктелері бір түзудің
бойында жатады.
D1 EC1
үшбұрышында екі қабырғасы мен үшінші медианасы
белгілі болғанда оны салуға болады. Бұдан соң үш қабырғасы бойынша
DD1 F және
FCC1
үшбұрыштарын салып,
DAED1 , және
BEC1C
параллелограмдарын салуға болады. Бұдан соң A және В нүктелері анықталады.
Салу.
DEC1
үшбұрышын
D1 E AD
және
CE1 BC, сондай-ақ EF
медианасы бойынша саламыз. Бұл үшін ең алдымен 2EF,
ED1 ,
EC1 , үш
қабырғасы бойынша үшбұрыш салып, оны параллелограмға дейін
толықтырамыз. Осы параллелограмның жартысы
D1 EC1 — үшбұрышы
болады. Қабырғалары
1 DC
2
және
1 AB
2
болатын өзара тең үшбұрыштар
D1 F
және
FC1
кесінділеріне салынады. Бұлар арқылы D және С нүктелерін
саламыз.
DAED1
және
BEC1C
параллелограмдарын салып, А және В
нүктелерін табамыз.
Дәлелдеу. ABCD төртбұрышы — ізделген төртбұрыш, себебі ол есептің барлық шарттарын қанағаттандырады. DF және FC бір түзудің бойында
жатыр, себебі
DFD1 CFC1 және
DF1 және C1 F
бір түзудің бойьшда жатыр.
Зерттеу.
ED1C1 үшбүрышын салу үшін
2EF AD BC
және
2EF
AD BC
шарттарының орындалуы қажетті, ал
DD1 F
және
FCC1 —
салу үшін
D F 1 ( AB CD) және D F
AB CD
шарттары орындалуы
1 2 1
қажетті. Егер бұл шарттар орындалса, онда есептің бір ғана шешімі бар болады.
Әдістемелік ұсыныстар: 1. Кеңістікте салуға берілген есепті шешуге кірісуден бұрын материалдың теориялық жағын меңгеріп алу қажет. 2. Салу есептерін шешуге кіріскенде алдымен қарапайым салулардан бастап шешу керек. 3. Есептер шешу кезінде әсіресе көрнекі құралдар мен модельдерді (нұсқаларды) пайдаланудың ерекше маңызы бар. 4. Негізгі салуларды дәл орындау керек: а) кеңістіктегі нүктенің орнын анықтау; б) берілген екі нүкте арқылы түзу жүргізу; в) бір түзудің бойында жатпайтын үш нүкте арқылы жазықтық жүргізу; г) түзу мен жазықтықтың қиылысу нүктесін табу; д) әрбір жазықтықта барлық планиметриялық салулардың орындалуы; е) егер өзін анықтайтын элементтер берілсе, онда геометриялық дене салу.
Егер кеңістікте салуға берілген есептердегі негізгі амалдар, яғни онда ұсақ бөліктерге бөлінетін негізгі қарапайым салулар түгел орындалса, онда кеңістіктегі кез-келген геометриялық салу орындалады деп есептеледі.
1 ... 6 7 8 9 10 11 12 13 ... 16
-
Планиметрия курсын үйрену әдістемесі.
-
Геометрия есептерін шешудіңәдістері. -
Стереометрия курсын үйренуәдістемесі.
-
Геометрияны оқытуда есептерді шеше білу дағдысын қалыптастыру және оны жалпы түрде дамыту аса маңызды мәселелердің бірі болып табылады. Геометриялық есептерді шешу туралы жалпы білік- дағдылар әдетте көптеген есептерді шешу арқылы қалыптасады. Олай болса, студент пен оқытушының не мұғалім мен оқушының жүйелі түрде ұзақ уақыт еңбектенуіне тура келеді. Шешілу жолы беймәлім, әр түрлі теориялық
Есептің шартын түсіну: а) есепті талдау; б) есеп шартын схема түрінде жазу. Есепті талдағанда оның шарты қандай, онда қандай талап қойылған (не берілген, не белгілі, есеп шарты неден тұрады?) екені анықталады. Есеп шартын схема түрінде жазғанда оның сызбасы қоса қарастырылады, осы талдаудың нәтижесінде есеп шартындағы ең керекті, таныс элементтер ескеріліп, олар қысқаша жазылады. Есепті талдау мен оның сызбасын және шартын схема түрінде қысқаша жазу — есепті шешу үшін жоспар іздеудің негізгі құралы болып табылады. Есепті талдай келе осы есепке қандай мөлшерде теориялық білімнің қажет болатындығы анықталады.
Есеп шешімін іздеу — есепті шешудің тәсілін іздеу, бұл бүкіл процестің негізгі бөлігі болып табылады. Бұл кезеңде ең алдымен берілген есептің түрі (типі), яғни оның дәлелдеуге, есептеуге не геометриялық түрлендіруге берілгені анықталады, осыған орай есепті шешу тәсілі ізделеді. Есеп шартында берілген элементтер мен іздеуге, анықталуға тиісті белгісіздер арасындағы байланыс ізделеді. Есеп шешімін іздеуде бір-бірімен тығыз байланысты мынадай екі жақты мәселені анықтайды: а) белгілі теориялық білімді шешілуге тиісті есеп шартына сай түрлендіру; б) есеп шартын белгілі теориялық фактілерге сәйкес және оларға байланысты түрлендіру. Бұл арада теориялық білім деп отырғанымыз математикалық ұғымдар мен олардың анықтамалары, теоремалар және математикадағы негізгі әдістер (координаттар әдісі, векторлық әдіс, геометриялық түрлендірулер мен теңдеулер құру әдісі және т.б.). Есептердің түрі мен құрылысына қарай оларды кластарға жіктеп талдау мен шешу әдістерін таңдап алады. Әсіресе, бірнеше теориялық материалдарды біріктіретін, әрі күрделі, әрі көптеген есептерді шешуге теориялық әдістемелік негіз болатын тірек есептерін талдау кезінде белгілі бір гипотеза ұсынылады және оның іске асырылуы тексеріледі. Есеп шешімін іздеу үшін гипотеза ұсына отырып,
Жоспарды іске асыру. Бұл арада шешу идеясы табылып, есеп шешіледі.
Шешілген есепті талқылау: а) есеп шешімін тексеру; б) есепті зерттеу; в) есеп шешімін әр түрлі параметрлер мен байланыстар бойынша талдау.
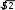 мысал. Тікбұрышты үшбұрыштың катеттеріне жүргізілген
мысал. Тікбұрышты үшбұрыштың катеттеріне жүргізілгенмедианалары
см және
см. Оның гипотенузасын табу керек (8-сурет).

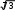 А
АЕ
С В
F
8-сурет
Шешуі. ВС мен AC катеттерін сәйкес х пен у ар-ылы белгілейік.
ВСЕ, ACF — тікбұрышты үшбүрыштар болғандықтан,
ВС 2 BE 2 EC 2
және
CF2
AF 2
-
AC
2 , яғни x
2
2 y
73
4
және
x 52 y2
2
4
. Бұл тендеулер жүйесін
шешіп, х пен у-ті табамыз:
 73 0,25y2 4 52 4y2 ,
73 0,25y2 4 52 4y2 ,y2 36 ;
y 6cм ,
х 8см;
АВ
10см .
мысал. ABC үшбұрышында АВ=26см, BC=30см, АС=28см. В төбесінен ВН биіктігі мен BD биссектрисасы жүргізілген. BHD үшбұрышының ауданын табу керек.
SAВС
0,5АС ВН
0,5 28 h 14h ; екінші жағынан
S АВС
336см2 .
Демек, 14h=336, h=24 см. Енді CD=x деп алып, ABC үшбұрышының ішкі бұрышы биссектрисасының қасиетін пайдаланайық: ВС:АВ=CD:DA, 30:26=x:(28-x), х=СD=15см; AD=28-15=13см. ВСН : СН 2 ВС 2 ВН 2 324,
CH=18 см, DH=CH-CD=18-15=3см, S=0,5
DH ВН
36см2 .
-
мысал. Медианалары
mb 9см ,
ma 12см ,
mc 25см
болатын
үшбұрыштың ауданын есептеу керек (9-сурет).
 С
СА
-
сурет
Шешуі.
ABC : mb BE 9см ,
ma AD 12см .
mc CF 15см. Берілген
элементтер мен іздеген элементтің арасындағы байланысты анықтайық (О — медианалардың қиылысу нүктесі).
AOC : AО 2 m 2 12 8см , OC 2 m
10см , OE 1 m
3см
3 a3
3 с 2 b
ОЕ медианасын екі еселеп, АОС үшбұрышын AOCB1
параллелограмына дейін толықтырайық. Сонда AC 2 OB2 2(AO2 OC2 ) ;
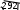 AC . Осы сияқты OD медиананы екі еселеп, ВОС үшбүрышын
AC . Осы сияқты OD медиананы екі еселеп, ВОС үшбүрышынпараллелограмға толықтырсақ:
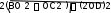
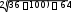
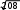 BC .
BC .Осылай қарастырып, АВ=10см екенін аламыз. Енді Герон
ABC
формуласымен ауданды есептесек, S 72см2 .
Осы есепті басқа әдіспен шешейік.
AOC мен
ABC -ның табандары тең
болғандықтан, S
1 S
Шынында да,
OME BNE ,
OM OE , ал
OE 1
AOC
3 AOC
BN BE
BE 3
болғандықтан,
OM 1 . Сондықтан
BN 3
SAOC SABC
OM
BN
1 ,
3
SAOC
1 S
3
ABC
Енді
AOCB1
параллелограмынан:
1
SAOC SOCB ;
p 12 ,
S 24см2 ,
S 72см2
-
Геометрия есептерін шешудің әдістеріне: а) геометриялық;
б) алгебралық; в) комбинациялық деп аталатын негізгі әдістер жатады.
Есептерді геометриялық әдіспен шешкенде логикалық ойлаудың жәрдемімен белгілі теоремалар арқылы тұжырымдауды қажетсінетін сөйлемдерді дәлелдейміз. Ал есептерді алгебралық әдіспен шешкенде ізделінген шаманы табу, не тұжырымдауға тиісті сөйлемді дәлелдеу тікелей есептеу жолымен немесе теңдеулер мен олардың жүйелерін құру арқылы іске асады. Тікелей есептеу әдісінің мәні мынада: есептің берілгендері мен белгісіздерінің жан-жақты байланыстарынан аралық қосымша белгісіз шамалар тізбегі құрылады, тізбекке қатысытын әрбір белгісіз шама анықталады немесе іздеген шама белгілі шамалар арқылы өрнектеледі.
-
- мысал. Теңбүйірлі ABC үшбұрышының табаны AC, төбесіндегі В бұрышы сүйір, С бұрышының биссектрисасы CD кесіндісі болсын. D нүктесі арқылы CD биссектрисасына перпендикуляр түзу жүргізілген. Бұл түзу үшбұрыштың AC табанымен немесе оның созындысымен Е нүктесінде қиылысады. AD =0,5ЕС болатынын дәлелдеу керек (10-сурет).
 В
ВF
D
Е А K С
-
сурет
Есеп геометриялық әдіспен тікелей шешіледі. CD кесіндісі — EFC үшбұрышының әрі биіктігі, әрі биссектриссасы. D нүктесін ВС қабырғасымен (CD EF және CD — С бұрышының биссектриссасы) қиылысқанша созсақ, EFC теңбүйірлі үшбұрышы шығады. Есептің шарты бойынша CD EF. Ендеше ED = DF. D нүктесінен ВС-ға параллель түзу жүргізсек, ол AC табанымен К нүктесінде қиылысады. Бұл DK кесіндісі EDC үшбұрышының медианасы бола алады. ЕК:КС = ED:DF = 1, бұлардан DK = 0,5ЕС, сондықтан AD = DK= 0,5 EC.
-
-мысал.Теңбүйірлі трапецияға іштей дөңгелек сызылған. Трапеция
ауданының дөңгелек ауданына қатынасы
-ге тең. Трапецияның үлкен
8
табанындағы сүйір бүрышын табу керек (11-сурет). ABCD — теңбүйірлі
трапециясы берілген,
Sдон : STP : 8 .
Бірінші тәсіл. Есептің мазмұнынан оны синтез әдісімен немесе алгебралық әдіспен шешуге болатынын байқаймыз. Синтез әдісі бойынша
r 2
0,5(a b) 2r
, 8
a b 8r,
r a b .
8
Екінші жағынан шеңберді сырттай сызылған төртбұрыштың қасиеті бойынша AD+BC=AB+DC теңдігін жаза аламыз. Бұдан 2AD=a+b,
AD=0,5(a+b). Тікбұрышты AED үшбұрышынан
sin A DE
AD
4r a b
; бұл
теңдікке r-дің мәнін қойып ықшамдасақ, sin A = 0,5 шығады. Сонымен,
A .
6
 A B
A BE
-
сурет
Бұл есепте жоғарыда айтылған тірек элементін және қосымша белгісіздер енгізу, теңдеу құру, қосымша белгісіздерді ығыстыру процестерінің барлығы орындалады.
Екінші тәcіл. 11-суреттен AD=BC теңдігін ескеріп, бір нүктеден шеңберге жүргізілген екі жанама тең болатынын пайдалансақ,
AN a ,
2
NN b,
2
sin A DE
AD
2r
AN ND
4r .
a b
r-дің 1-тәсілдегі мәнін орнына қойсақ, sinA = 0,5, бұдан
A .
6
Теңдеулер құру арқылы шешілетін есептерді қарастыралық.
6-мысал. Тікбұрышты үшбұрыштың гипотенузасы с-ға тең, үшбұрыштың бір сүйір бұрышынан катеттерінің біріне ұзындығы m-ге тең медиана жүргізілген. Осы үшбұрыш катеттерінің ұзындықтарын табу керек (12-сурет).
 В
ВD
С А
12-сурет
бойынша:
АС 2 ВС 2 AB 2 ,
АС 2 СD2 AD2
немесе
x2 y2 c2 ,
x2
(0,5y)2
m2 . Бұл жүйенің шешімі
BC 2
, AC .
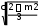
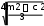 Математикалық есептердің көбінде қосымша белгісіздер енгізу әдісі қолданылады. Бұл есептердің берілген элементтері мен қажетті теориялық материалдарды байланыстыруға септігін тигізеді. Есепті шешу барысында осы қосымша белгісіздер ығысады.
Математикалық есептердің көбінде қосымша белгісіздер енгізу әдісі қолданылады. Бұл есептердің берілген элементтері мен қажетті теориялық материалдарды байланыстыруға септігін тигізеді. Есепті шешу барысында осы қосымша белгісіздер ығысады.7-мысал. Ромб биіктігі оның қабырғасын m және n бөліктерге бөледі.
Ромб диагоналдарының ұзындықтарын табу керек (13-сурет).
 С
СА
13-сурет
-
тәсіл. Теңдеулер құруға қажетті белгісіздер енгізелік. Ол үшін АС=x,
BD=y деп белгілейміз. Сонда
АВ AE EB m n.
Бұл қосымша элементті
есеп шартындағы белгілі және белгісіз шамалар арқылы өрнектейміз. ЕD h
десек,
h2 y2 n2
және
h2 (m n)2 m2.
h2 -тың мәндерін теңестірсек,
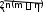 у2 n2 (m n)2 m2, х-ті табамыз:
у2 n2 (m n)2 m2, х-ті табамыз:y 2 2mn 2n2
немесе
y . АОВ үшбұрышынан
 АО2 AB2 OB2 (m n)2 (0,5
АО2 AB2 OB2 (m n)2 (0,5 AC x 2AO
AC x 2AO 2n(m n))2 ,
.

 Сонда жауабы: 2n(m n), .
Сонда жауабы: 2n(m n), .-
тәсіл. Аудандарды пайдалану әдісі бойынша
0,5d1d2
шамасын

 қосымша элементтер арқылы табылатын ауданға теңестіреміз, яғни
қосымша элементтер арқылы табылатын ауданға теңестіреміз, яғни0,5d1d2 (m n)
2n(m n) , мұндағы
h 2n(m n) . АОВ үшбұрышынан
(0,5d )2 (0,5d )2 (m n)2 немесе d 2 d 2 4(m n)2 . Бірінші теңдіктің екі
1 2 1 2

 жағында 4-ке көбейтіп екінші теңдікке қоссақ, онда
жағында 4-ке көбейтіп екінші теңдікке қоссақ, онда1 2
(d d )2 4(m n)
4(m n)2 4(m n)(
m n).
Бірінші теңдіктен d1 -ді тапсақ және оны соңғы теңдікке қойсақ,
түрлендіргеннен кейін
d болады. Енді d 2 4(m n)2 d2
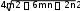
 2 1 1
2 1 1теңдігіне
d 2 -нің табылған мәнін қойсақ,
d1 екені шығады. Егер
берілген есепте кейбір шамалардың (ұзындықтардың немесе аудандардың) қатынастарын табу қажет болса, дербес жағдайда белгілі бір бұрышты есептеу қажет болса, ондай есептер көмекші параметр енгізу деп аталатын тәсілмен шешіледі. Бұл тәсіл бойынша есепті шешу үшін сызықтық
-
Мектеп оқушыларының кеңістікті қабылдап, оны көз алдына елестете алуы стереометрияны оқытудың негізгі мәселелерінің бірі болып саналады. Осы айтылған мақсатты іс жүзіне асыруда кеңістіктегі салуға берілген есептерді шешудің зор мәні бар. Жазықтықтағы геометриялық салулар теориясы жеткілікті түрде талқыланып қарастырылады, ал стереометрияның әдістемелік мәселелеріне әлі де толық көңіл бөлінбей келеді. Геометриялық салулар теориясы – салуды негіздеу, есептерді кластарға жіктеу, есеп шешу әдістері, белгілі бір класқа жататын есептерді шешу критериі, салу есептерін шешкенде барынша жай әдістерді тиімді қолдану сияқты мәселелерді қарастырады.
мысал. Берілген а және b түзулеріне паралелль, берілген А нүктесінен өтетін жазықтық жүргізу керек.
Талдау. Іздеген жазықтық а түзуіне паралелль а1
түзуі арқылы өтуі
керек. Дәл осы сияқты іздеген жазықтық b түзуіне паралелль b1
түзуі арқылы
өтуі керек. а1
және b1
түзулері А нүктесі арқылы өтуі керек.
Салу. 1. А нүктесі және а түзуі арқылы жазықтығын жүргіземіз. 2.
жазықтығында А нүктесі арқылы а түзуіне паралелль а1
түзуін
жүргіземіз. 3. А нүктесі және b түзуі арқылы жазықтығын жүргіземіз. 4.
жазықтығында А нүктесі арқылы b түзуіне паралелль b1 түзуін жүргіземіз. 5.
а1 және b1
түзулерінен бір-бірден М және N нүктелерін таңдап аламыз. 6. А,
М, N нүктелері арқылы іздеген а жазықтығын жүргіземіз.
Дәлелдеу. 1. Салуымыз бойынша
а1 а
және
а1 . яғни,
а
. 2.
b1 b -бұл салуымыз бойынша және
b1 . Демек,
b
. 3.
A a1
және
A b1 .
сонда, A.
Зерттеу. А нүктесінің а немесе b түзулерінде жатуына тәуелсіз есептің әрқашан шешімі болады. Егер а мен b түзулері паралелль болмаса,
онда есептің бір ғана шешімі бар болады. Ал көп шешуі бар болады.
а b
болса, онда есептің сансыз
-
мысал. Барлық төрт қабырғасы және қарама-қарсы екі қабырғасының орталарын қосатын кесінді берілген жағдайда ABCD төртбұрышын салу керек (14-сурет).
 D С
D СC1
14-сурет
Шешуі. ABCD — ізделген тертбұрыш, EF — АВ және DC қабырғаларының орталарын қосатын кесінді болсын. AD қабырғасын
 параллель жылжытып
параллель жылжытыпED1
және ВС қабырғасын параллель жылжытып
EC1
жағдайына келтіреміз, сонда
DD1 AE ,
DD1
AE ; CC1 BE ,
CC1
BE , DF CF —
бұлар шарт бойынша, демек,
DD1 F FC1C
(екі қабырғасы және олардың
арасындағы бұрышы бойынша тең). Бұл үшбұрыштардың теңдігінен
DFD1 CFC1
шығады. Демек,
D1 , F және
C1 — нүктелері бір түзудің
бойында жатады.
D1 EC1
үшбұрышында екі қабырғасы мен үшінші медианасы
белгілі болғанда оны салуға болады. Бұдан соң үш қабырғасы бойынша
DD1 F және
FCC1
үшбұрыштарын салып,
DAED1 , және
BEC1C
параллелограмдарын салуға болады. Бұдан соң A және В нүктелері анықталады.
Салу.
DEC1
үшбұрышын
D1 E AD
және
CE1 BC, сондай-ақ EF
медианасы бойынша саламыз. Бұл үшін ең алдымен 2EF,
ED1 ,
EC1 , үш
қабырғасы бойынша үшбұрыш салып, оны параллелограмға дейін
толықтырамыз. Осы параллелограмның жартысы
D1 EC1 — үшбұрышы
болады. Қабырғалары
1 DC
2
және
1 AB
2
болатын өзара тең үшбұрыштар
D1 F
және
FC1
кесінділеріне салынады. Бұлар арқылы D және С нүктелерін
саламыз.
DAED1
және
BEC1C
параллелограмдарын салып, А және В
нүктелерін табамыз.
Дәлелдеу. ABCD төртбұрышы — ізделген төртбұрыш, себебі ол есептің барлық шарттарын қанағаттандырады. DF және FC бір түзудің бойында
жатыр, себебі
DFD1 CFC1 және
DF1 және C1 F
бір түзудің бойьшда жатыр.
Зерттеу.
ED1C1 үшбүрышын салу үшін
2EF AD BC
және
2EF
AD BC
шарттарының орындалуы қажетті, ал
DD1 F
және
FCC1 —
салу үшін
D F 1 ( AB CD) және D F
AB CD
шарттары орындалуы
1 2 1
қажетті. Егер бұл шарттар орындалса, онда есептің бір ғана шешімі бар болады.
Әдістемелік ұсыныстар: 1. Кеңістікте салуға берілген есепті шешуге кірісуден бұрын материалдың теориялық жағын меңгеріп алу қажет. 2. Салу есептерін шешуге кіріскенде алдымен қарапайым салулардан бастап шешу керек. 3. Есептер шешу кезінде әсіресе көрнекі құралдар мен модельдерді (нұсқаларды) пайдаланудың ерекше маңызы бар. 4. Негізгі салуларды дәл орындау керек: а) кеңістіктегі нүктенің орнын анықтау; б) берілген екі нүкте арқылы түзу жүргізу; в) бір түзудің бойында жатпайтын үш нүкте арқылы жазықтық жүргізу; г) түзу мен жазықтықтың қиылысу нүктесін табу; д) әрбір жазықтықта барлық планиметриялық салулардың орындалуы; е) егер өзін анықтайтын элементтер берілсе, онда геометриялық дене салу.
Егер кеңістікте салуға берілген есептердегі негізгі амалдар, яғни онда ұсақ бөліктерге бөлінетін негізгі қарапайым салулар түгел орындалса, онда кеңістіктегі кез-келген геометриялық салу орындалады деп есептеледі.