Файл: Алпысов А.. Математиканы оыту дістемесі оу ралы Павлодар, 2012.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 1785
Скачиваний: 140
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. Математиканы оқыту әдістемесі пәні
2. Математиканы оқытудың мақсаттары мен мазмұны
Математиканы оқытудың қағидалары
Математиканы оқытудың әдістері
5. Математикалық ұғымдар, сөйлемдер және оларды үйренудің әдістемесі
6. Математиканы есептер арқылы оқыту әдістемесі
Математикадан сыныптан тыс жұмыстар, оны өткізу әдістері
9. Педагогикалық практика туралы
Анализ (грекше analygts) – жіктеу, бөлшектеу, талдау дегенді білдіреді. Синтез (грекше sinthesis) – біріктіру, жинақтау, теру дегенді білдіреді.
Синтез деп жеке элементтерді бір тұтасқа жинақтауға көмектесетін логикалық тәсіл. Математиканы оқытуда анализ бен синтез мәні өте зор, ол есептерді шешу әдісі ретінде, теореманы дәлелдеу, математикалық ұғымдардың қасиетін үйрену т.б. әр алуан формада кездеседі.
Анализ бен синтез – іс жүзінде бірін-бірі толықтыратын бір тұтас аналитикалық – синтетикалық әдіс. Мәселен, анализ кезінде күрделі есептер жай есептерге бөлшектенеді, ал синтез жай есептерді бір ғана мағыналы, бір тұтас бір есепке біріктіреді. Анализді бүтіннен оның құрамды бөліктеріне жіктейтін ойлау әдісі, ал синтез – жеке бөліктерді бір бүтінге біріктіретін ойлау әдісі деп түсінеміз. Анализ бен синтез математиканы оқыту процесінде ұғымдарды қалыптастыруға, теоремаларды дәлелдеуде және есептерді шығаруда кеңінен пайдаланады. Анализ бен синтез математиканы оқып – үйренудің аса маңызды әдістері болып табылады. Олардың қолдануларын көрсететін мысалдар қарастырамыз:
Мысалы. Үшбұрыштың ішкі бұрыштарының қосындысы 2d болатынын дәлелдеу керек.
-
Аналитикалық жолмен дәлелдеу тәсілі. 2d – жазық бұрыш кез келген үшбұрыштың үш бұрышы жазық бұрышқа орналасатынын көрсету керек (4-сурет).
а) М- нүктесінен өтетін CK||AB болатын жазыңқы бұрышты саламыз. б) 2 жазбадан бірден табылады.
в) 5 1, CK||AB, М-қиюшы.
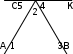
М
5-сурет
г) 4 3
д) 5 4 2 2d
е) 1 2 3 2d
-
Синтетикалық жолмен дәлелдеу тәсілі.
а) CK||AB жүргіземіз.
б) 4 3, CK||AB, ВМ-қиюшы.
в) 5 1, CK||AB, АМ-қиюшы.
г) 5 4 2 2d
д) 1 2 3 2d
жазыңқы бұрыш.
Стереометрия есептерін шешуге анализ бен синтезді қолдану.
Мысалы. Призманың табаны ұзындығы 3м болатын тең қабырғалы үшбұрыш. Бүйір қабырғасы 5м, ол табан қабырғаларымен бұрыш жасайды. Призма көлемін табу керек (6-сурет).
В1
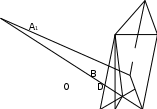 С1
С1А E С
6-сурет
Берілгені: АВСА1 В1С1 үшбұрышты призма.
АВС : АВ
ВС
АС
3м
А1 АВ А1 АС .
А1 А 5м
Т.к V=?
Аналитикалық әдіс: Призма көлемі V SH
h=? S=?
(1)
 A OE : АО (2)
A OE : АО (2)1 1
A EA : A EA 900 , A AE ,
АА 5м
Мұнда
1 1 1
АЕ1 5sin
1
(3)
АЕ 5cos (4)
АЕО : AEО 900 , ОAЕ 300 бұдан ОЕ АЕtg 300
ОЕ 5cos tg300 (5)
(3) және (5) мәнін (2)-ге қойсақ,
 А1О (5cos) (5cos tg30 ) ,
А1О (5cos) (5cos tg30 ) ,2 0 2
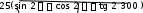
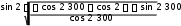 А1О
А1О 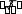
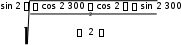 5
5
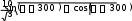 (6)
(6)ABC ның ауданын табу үшін оның қабырғаларының ұзындығын табу керек.
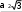
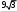 S
S 4 4
(7)
-
және (7) мәндерін (1)-ге қоямыз:
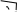
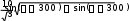
 V 9 3
V 9 3 4
куб бірлік.
Синтетикалық әдіс: Қосымша салу жұмысын жүргіземіз:
а) AD-биссектриса
ВАС, б)
А1О АС,ОЕ А1Е А1 Е АС
А1 ЕА :
А1 Е
5sin
(1),
АЕ 5cos
(2)
ОЕ 5cos tg300
(3)
А1ОЕ :
А1О
(4)
-
 және (3) мәндерін (4)-ке қоямыз:
және (3) мәндерін (4)-ке қоямыз:
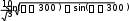 А1О
А1О ABC : S
( AC)2
2
sin 600
 4
4
 V 9 3 10
V 9 3 104 30
sin( 300 ) sin( 300 ),
 V 45
V 452
sin( 300 ) sin( 300 )
куб бірлік.
Синтетикалық әдіс арқылы есептерді шешу және теоремаларды дәлелдеу барысын қысқа да ықшамды тұжырымдауға мүмкіндік береді. Мұнда кейбір жағдайларда синтетикалық жолмен баяндауды аналитикалық тәсілмен ауыстырып отыру керек. Бұл оқушылардың танымдық қызметін белсендіреді және есептерді шешу жолдарын саналы түрде іздестіре отырып, сапалы түрде түсінуіне мүмкіндік береді.
-
Индукция (лат. Inductio-ой салу) - жеке фактілер жайындағы ғылыми білімнен немесе дербес білімнен жалпы білімге, тәжірибелік нәтижелерден теориялық жалпылау мен қорытындыға, жекеден жалпыға, белгіліден белгісізге қарай қозғалудың логикалық әдісі.
Мысалы, 1+3=4, 5+7=12, 9+11=20, …, . Бұл мысалдардан «екі тақ санның қосындысы жұп сан болады» және 2+4=6, 6+8=14, 8+10=18, 12+14=26, … . «екі жұп санның қосындысы жұп сан болады» деген қорытындылар жасаймыз. Сонымен дербес фактілерден жалпы қорытындылар жасау әдісін индукция дейді.
Индукция әдісі – математиканы баяндауға таңдап алынған аксиоманың негізіне жатады. Аксиомалар математикалық тұжырымдамалардың дұрыстығын анықтауға көмектеседі. Белгілі бір теореманың дұрыстығы ғасырлар бойы қалыптасқан дәстүр бойынша күнделікті тұрмыста кездесетін тәжірибемен көрнекі түсініктердің негізінде дәлелденеді, тек осыдан кейін ғана оған дедуктивтік қорытынды жасалады. Сондықтан индукция әдісіне қарағанда дедукция әдісі күрделірек. Орта мектептердің сыныптарында индукция, ал жоғары сыныптарында дедукция көбірек қолданылады. Ғылыми зерттеу жұмыстарындағы күрделі есептермен орта мектептегі есептерді, әртүрлі мәселелерді шешуге индукция мен дедукция қатар қолданып бірін–бірі толықтырады.
Дедукция теориялық мәселелер формальды сипатталатын білімдер облысында (мысалы, математикада) үлкен роль атқарады.
Дедукция – жалпыдан жалқыға, бүтіннен бөлшекке көшетін пайымдау жолы.
Дедукция – ғылыми–зерттеу әдісі. Дедукция кейбір берілген тұжырымдарға сүйеніп, тікелей логикалық тұрғыда қорытынды жасалатын ойлау формасы.
Мысалы. «Кез келген натурал санның цифрларының қосындысы үшке бөлінсе, онда санның өзі де үшке бөлінеді» деген тұжырым дұрыс.
Дедуктивтік ой қорытудың, мынадай түрлері бар:
-
Неғұрлым жалпы қағидадан жеке қағидаға қарай апаратын ой қорытындылары. Мәселен, НОД (р, q)=1 мысалы осының дәлелі. -
Жалпы қағидадан жалпы қағидаға апаратын ой қорытындысы.
Мысалы. Барлық жұп сандар 2-ге бөлінеді. Барлық тақ сандар 2-ге бөлінбейді.
-
Жеке қағидадан дербес қағидаға апаратын ой қорытындылары.
Мысалы. 5-жай сан. 5-натурал сан. Кейбір натурал сандар жай сан болады.
Дедукция әдісін ежелгі грек ғалымдары қалыптастырған. Б.э.д. ІІІ ғасырда ертедегі грек геометрі Евклид жазған «Негіздер» кітабы теорияны дедуктивтік түрде құрастырудың ең тамаша үлгісі болды. Осы үлгіде математикалық шығармалар мен қатар философиялық трактаттарда жазылды. Дедукция әдісімен жасалған қорытынды дұрыс болуы үшін әуелгі негізгі мағлұмат дұрыс дәлелденген болуы керек, сонда бұлардан шығатын қорытындылар дұрыс болады. Дедукция ретінде алынатын аксиомалар жүйесін дедукциялық әдіс дейді. Осы әдіспен ХІХ ғасырда геометрияның толық аксиомалар жинағы құрылды. Неміс математигі Д.Гильбердтің
«Геометрияның негіздерінде» негізгі ұғымдарға нүкте, түзу, жазықтық,
ал олардың арасында негізгі қатынасқа «жататындығы», «арасында жататындығы», «конгруэнтті» болуы алынады. Қазіргі мектепте нүкте, түзу, жазықтық, арақашықтық сияқты негізгі ұғымдар алынған басқаша аксиомалар жүйесі қолданылады. Геометрия қандай аксиомалар жүйесіне негізделсе де бәрі бір оның қалған сөйлемдері, ұғымдары мен теоремалары таңдап алынған аксиомаларға сүйеніп құрылады. Теореманы дәлелдеуге нақты үшбұрыштардың қабырғаларының ұзындығы мен бұрыштарының шамасын өлшеу нәтижелеріне сүйенуге болмайды. Бұл дәлелдеулер таза логикаға сүйеніп дедуктивті түрде қорытындыланды. Дедуктивтік зерттеу жұмысы барысындағы жалпы қағидалар және заңдар ғылымдардың жаңылыс жолға түсіп кетпеуіне, шындық дүниесінің құбылыстарын дұрыс түсінуге мүмкіндік береді. Бірақ осы негізде дедуктивтік әдістің ғылыми мәнін асыра бағалау да дұрыс болмаған еді. Дедуктивтік ой қорытулар үшін бастапқы білімдер керек болады. Міне осы кезде дедукцияға индукция жәрдемге келеді. Сондықтан индукция және дедукция бірін-бірі толықтырып, өзара тығыз байланыста болады.
Индукция әдісі толымсыз, толық, математикалық болып үшке бөлінеді. Толымсыз индукция деп қарастырылатын жағдайлар өте көп болып, олардың барлығын түгел зерттеу мүмкін болмаған жағдайда, олардың тек кейбіреулерін ғана зерттеп солардан шығатын қорытындыны барлық фактілер үшін жасалатын қорытындыны айтамыз. Мысалы, 1=12, 1+2=32, 1+3+5=32 , 1+3+5+4=42 ,..., теңдіктерін бірден есептеу арқылы олардың дұрыстығына көз жеткіземіз. Осы дербес мағлұматтарға сүйеніп 1+3+5+7+9+…(2k-1) =k2 деген жалпы қорытынды жасаймыз.
Толық индукция деп математикада қарастырылатын жағдайларының саны шектеулі, ол жағдайлардың бәрін түгел қарастырып барып қорытынды жасауға болатын жағдайларды айтады.
Мысалы, кез келген дұрыс көпжақ үшін Т+Қ+Ж=2 (1) қатысы дұрыс болады. Мұндағы Т - көпжақтың төбесінің саны, Қ- қабырға саны, Ж- көпжақтың жақ саны. Тетраэдр, октаэдр, куб, додекаэдр, икосаэдр сияқты бес дұрыс көпжақты қарастырумен шектелеміз. Басқа дұрыс көпжақ болмайды. Кесте бойынша тексерейік:
| көпжақтың аты | төбе саны | қабырға саны | жақ саны |
| Тетраэдр | 4 | 6 | 4 |
| октаэдр | 6 | 12 | 8 |
| куб | 8 | 12 | 6 |
| додекаэдр | 20 | 30 | 12 |
| икосаэдр | 12 | 30 | 20 |