ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 153
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рис. 3.1. График зависимости
Mтр
f(d)
началом отсчета по каждой оси (рис.3.1).
-
Возле каждого конца осей координат указывается измеряе- мая физическая величина с множительным коэффициентом и
единиц измерений, например
Mтр 103,
Н м
или
Mтр ,
103
Н м
-
это эквивалентные формы записи обозначе-
ний осей, что соответствует тому, что число, соответствующее
точке на оси координат, необходимо разделить на 103
-
в первом
варианте, чтобы получить измеренную величину
Mтр
5,6 103 Н м, а во втором – умножить на 103
(рис. 3.1).
-
Через экспериментальные точки проводится линия таким
образом, чтобы сумма квадратов расстояний Si
от эксперимен-
тальных точек до линии принимало минимальное значение
n
S
i
i1
2 min. В программе Microsoft Excel этой линией является
линия тренда, для которой определяется уравнение кривой и ко-
эффициент корреляции проксимации.
R2 или коэффициент достоверности ап-
-
ЛАБОРАТОРНАЯ РАБОТА № 1.
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА ВРАЩЕНИЯ
И МОМЕНТА СИЛ ТРЕНИЯ В ОПОРЕ
-
Цель работы-
Освоение экспериментального метода определения мо- мента инерции тела с массой, равномерно распределённой отно- сительно оси вращения, и момента сил трения в опоре. -
Ознакомление с методом оценки силы натяжения нити ûв рывке§.
-
-
Подготовка к работе
Прочитать в учебниках следующие параграфы: [1] – øø 3.4, 4.1 – 4.3; [2] – øø 13, 16 – 18; [3] – øø 35, 36. Для выполнения ра- боты студент должен: а) знать законы динамики поступательного и вращательного движения и закон изменения энергия; б) уметь пользоваться измерительными приборами.
-
Выполнение работы
-
Описание лабораторной установки
-
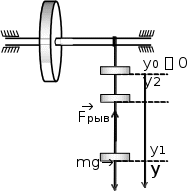 Лабораторная уста- новка представляет собой маховик с валом, на кото- ром подвязана нить с гру- зом (рис. 4.1).
Лабораторная уста- новка представляет собой маховик с валом, на кото- ром подвязана нить с гру- зом (рис. 4.1).Нить наматывается на вал до тех пор, пока нижнее основание груза не поднимется до уровня со- ответствующего коорди-
нате
y0 0 . Механическая
энергия груза в этом со- стоянии (начальная ско-
рость 0 ) равна его по-
тенциальной энергии mg( y1 y0 ) , механическая энергия рассматриваемой системы равна
Рис.4.1.Схемаустановки
Ε1 mg( y1 y0 ) Εрм mgy1 Eрм .
Предоставим грузу возможность опускаться. Через время t1
нить полностью разматывается, нижнее основание груза достига-
ет координаты
y1, скорость груза и угловая скорость махо-
вого колеса с валом принимает свои максимальные значения
2 y1 / t1; (4.1)
2 y1 /(Rt1) . (4.2)
В точке с координатой
y1 груз на мгновение останавлива-
ется, а маховое колесо продолжает вращаться в ту же сторону. Это приводит к тому, что происходит переброс нити на валу, и груз начинает подниматься вверх. Пренебрегая изменением угло- вой скорости за время, в течение которого маховое колесо пово- рачивается на угол, равный π (и направление скорости движения
груза изменяется на противоположное), можно оценить время Δτ переброса нити на валу (время ûрывка§ груза)
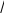 R. (4.3)
R. (4.3)При движении груза вверх маховое колесо вращается замед-
ленно, и через время t2
маховое колесо и груз останавливаются.
Нижнее основание груза при этом имеет координату
y2 , и меха-
ническая энергия системы при этом равна
E3 :
E3 mg( y1 y2 ) Eрм . (4.4)
- 1 2 3 4 5 6 7 8 9 ... 13
Экспериментальное определение момента инерции маховика с валом
-
Измерьте координату y1, радиус вала R; масса груза,
подвешенного на нити – m1; масса груза
m2 m1 m1, где
m1
– масса первого дополнительного груза; масса груза
m3 m2 m2 , где m2 – масса второго дополнительного груза.
Значения
y1, Rи m занесите в табл. 4.1 и 4.2.
-
Для каждого груза произведите не менее пяти измере-
ний времени
t1 опускания груза и координаты
y2 (измерения ко-
ординаты
y2 будут более точными, если маховик в момент оста-

 новки зафиксировать рукой); результаты измерений занесите в
новки зафиксировать рукой); результаты измерений занесите в
 табл. 4.1; найдите средние значения t1 и сите в табл. 4.2.
табл. 4.1; найдите средние значения t1 и сите в табл. 4.2.y2 .Результаты зане-
Таблица4.1
Результатыизмеренийвремениопускания грузаt1
икоординатыy2
| № п/п | m1= кг | m2 = | кг | m3 = кг | ||
| t1 | y2 | t1 | y2 | t1 | y2 | |
| с | м | с | м | с | м | |
| 1 | | | | | | |
| 2 | | | | | | |
| 3 | | | | | | |
| 4 | | | | | | |
| 5 | | | | | | |
| среднее | | | | | | |
| | y0 = | м | y1 = | м | R= | м |
-
По формуле
I 2 2
y1 y2
mRgt1
y1(2 y1
-
y2
1
)
вычислите момент инерции Iмаховика с валом; найдите среднее

 значение I.
значение I.Таблица 4.2Результатырасчетамоментасилытренияисилы натяжения



 нитив¶рывкеß
нитив¶рывкеß| № п/п | m | t1 | y2 | I | Mтр | Fрыв |
| кг | с | м | кг¬м2 | Н·м2 | Н | |
| 1 | | | | | | |
| 2 | | | | | | |
| 3 | | | | | | |
| I= кг¬м2 | Mтр = Н¬м2 | |||||
-


 Определите максимальную кинетическую энергию груза и максимальную кинетическую энергию маховика с валом;
Определите максимальную кинетическую энергию груза и максимальную кинетическую энергию маховика с валом;