Файл: Связи и массовых коммуникаций российской федерации федеральное государственное.docx
Добавлен: 09.11.2023
Просмотров: 227
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Часть 2. Точечные оценки исследуемого процесса
Задание 4. Формирование оценки выборки сигнала
В десяти независимых измерениях температуры процессора, установленного на компьютере, получены следующие значения:
Таблица 4.1
| Температурные значения процессора Тi | 38.6 | 48.2 | 45.3 |
| ni | 2 | 5 | 3 |
| n | 10 | ||
Задание 4.1
Вычислить значение выборочной дисперсии по данному распределению выборки (таблица 4.1).
Вычислить значение выборочной дисперсии по данному распределению выборки по следующим данным - таблица 4.2.
Таблица 4.2
| Температурные значения процессора Тi | 31,1 | 28,6 | 27,2 |
| ni | 3 | 4 | 3 |
| n | 10 | ||
Задание 4.2
Вычислить значение исправленной выборочной дисперсии по данному распределению выборки: таблица 4.1 и таблица 4.2.
Выполнение работы
Задание 4.1.
В программной среде MS Excel вычислим значения выборочной дисперсии по данному распределению выборки для таблиц 4.1. и 4.2.
Условие задания в MS Excel будет выглядеть так:
Таблица 4.1.
| варианта выборки | частота встречаемости xi | количество значений в выборке |
| xi | ni | n |
| 38,6 | 2 | 10 |
| 48,2 | 5 | 10 |
| 45,3 | 3 | 10 |
Таблица 4.2.
| варианта выборки | частота встречаемости xi | количество значений в выборке |
| xi | ni | n |
| 31,1 | 3 | 10 |
| 28,6 | 4 | 10 |
| 27,2 | 3 | 10 |
Найдем для обеих таблиц несмещенную оценку генеральной средней, определяемую по выражению:
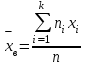
где xi варианта выборки; ni частота встречаемости варианты xi в выборке, и количество значений (вариант) в выборке определяется выражением:
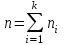
Формула для среды MS Excel будет выглядеть так:
=СУММ(A3*B3+A4*B4+A5*B5)/C3
Для таблицы 4.1. значение хв=45.41, для таблицы 4.2. значение хв=28.93.
Далее найдем Смещенной оценкой генеральной дисперсии служит выборочная средняя, определяемая по выражению:
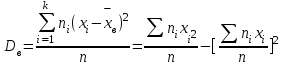
Проведем для подсчета значений выборочной дисперсии по данному распределению выборки промежуточные расчеты и получим итоговые цифры в графе Dв.
| Для таблицы 4.1. | |
| Σ ni*xi | 454,1 |
| Σ ni*xi^2 | 20752,39 |
| хв | 45,41 |
| Dв | 13,1709 |
| Для таблицы 4.2. | |
| Σ ni*xi | 289,3 |
| Σ ni*xi^2 | 8392,99 |
| хв | 28,93 |
| Dв | 2,3541 |
Использованные формулы:
Σ ni*xi = СУММ(A3*B3+A4*B4+A5*B5)
Σ ni*xi^2 =A3^2*B3+A4^2*B4+A5^2*B5
Dв = (I4/C3)-(I3/C3)^2
Задание 4.2
Вычислим значение исправленной выборочной дисперсии по данному распределению выборки для таблиц 4.1 4.2. по формуле:
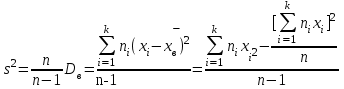
| | Табл. 4.1. | Табл. 4.2. |
| S2 | 14,63433 | 2,615667 |
Где формула s2 будет иметь вид:
=(I4-(I3^2/C3))/(C3-1)
Вывод: В программной среде MS Excel удобно считать дисперсию и математическое ожидание. Можно сделать промежуточный вывод: чем меньше значения в выборке и частота встречаемости ближе к средним значениям, тем меньше будет дисперсия и математическое ожидание.
Задание 5. Формирование оценки коррелированности сигналов
На приемник поступают два сообщения – два сигнала, описываемые выражениями (5.1) и (5.2). Требуется установить степень тождественности – схожести сигналов. С этой целью проводится вычисление корреляционной функции.
Задание 5.1
Вычислить значение коэффициента корреляции для выборочных значений двух сигналов, заданных выражениями:
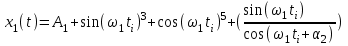 | 5.1.1 |
При условии: А1= 0 ; 1 = 480 ; i= 1,2,3,……. ,52; 1 = 0
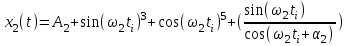 | 5.1.2 |
При условии: А2= 50 ; 2 = 240,260,280, ……520 ; i= 1,2,3,……. ,52; 2 = 0
Задание 5.2
Вычислить значение коэффициента корреляции для выборочных значений двух сигналов, заданных выражениями:
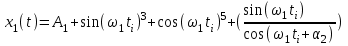 | 5.2.1 |
При условии: А1= 0 ; 1 = 480 ; i= 1,2,3,……. ,52; 1 = 0
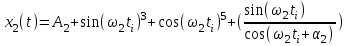 | 5.2.2 |
При условии: А2= 50 ; 2 =480; i= 1,2,3,……. ,52; 2 = 0,25;0.5;0.75;……;4.0
Выполнение работы
Задание 5.1.
Зададим условия задачи в программном комплексе MS Excel:
| n=52 | | Дано | | | | | | Уравнение 1 | Уравнение 2 |
| i | ti | A1 | A2 | w1 | w2 | a1 | a2 | x1 | x2 |
| 1 | 1 | 0 | 50 | 480 | 240 | 0 | 0,25 | -0,851564138 | 62,41431966 |
| 2 | 2 | 0 | 50 | 480 | 260 | 0 | 0,5 | -4,939554198 | 47,1471624 |
| 3 | 3 | 0 | 50 | 480 | 280 | 0 | 0,75 | 3,010221716 | 46,64249366 |
| 4 | 4 | 0 | 50 | 480 | 300 | 0 | 1 | -0,112228301 | 50,83580917 |
| 5 | 5 | 0 | 50 | 480 | 320 | 0 | 1,25 | 0,740368682 | 48,00739471 |
| 6 | 6 | 0 | 50 | 480 | 340 | 0 | 1,5 | -0,835392049 | 48,22782896 |
| 7 | 7 | 0 | 50 | 480 | 360 | 0 | 1,75 | -15,97330416 | 49,94570095 |
| 8 | 8 | 0 | 50 | 480 | 380 | 0 | 2 | 2,092880607 | 47,88467131 |
| 9 | 9 | 0 | 50 | 480 | 400 | 0 | 2,25 | -0,491180874 | 51,47049364 |
| 10 | 10 | 0 | 50 | 480 | 420 | 0 | 2,5 | 0,316077786 | 49,76824668 |
| 11 | 11 | 0 | 50 | 480 | 440 | 0 | 2,75 | -1,042721364 | -10,89102851 |
| 12 | 12 | 0 | 50 | 480 | 460 | 0 | 3 | 8,061457451 | 48,88530071 |
| 13 | 13 | 0 | 50 | 480 | 480 | 0 | 3,25 | 1,556084037 | 49,37408044 |
| 14 | 14 | 0 | 50 | 480 | 500 | 0 | 3,5 | -0,824653561 | 49,80088825 |
| 15 | 15 | 0 | 50 | 480 | 520 | 0 | 3,75 | -0,238191451 | 50,28749007 |
| 16 | 16 | 0 | 50 | 480 | 540 | 0 | 4 | -1,730171872 | 44,23961367 |
Поскольку t не задано, будем измерять его с интервалом 1 секунду в течение 52 секунд (в готовом модуле можно задать любое значение t), а уравнения 1 и 2 зададим выражениями:
=C3+SIN(E3*B3)^3+COS(E3*B3)^5+((SIN(E3*B3))/(COS(E3*B3+G3)))
=D3+SIN(F3*B3)^3+COS(F3*B3)^5+((SIN(F3*B3))/(COS(F3*B3+H3)))
Для вычисления коэффициента корреляции, по условию задания, нам потребуется провести несколько промежуточных расчетов.
Вычисление x1 и x2 среднего проведем по формуле:

Формула будет иметь вид: =СРЗНАЧ(I3:I54).
Далее подсчитаем столбец xi-xв для каждого уравнения и выведем в итогах столбца сумму по столбцу. Это необходимо для вычисления значения дисперсии, определяемой по формуле:
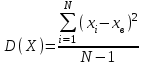
| x1-x1 cp | x1-x1 cp^2 |
| -0,81406 | -0,8529707 |
| -4,93955 | -4,9395542 |
| 3,010222 | 3,01022172 |
| -0,11223 | -0,1122283 |
| 0,740369 | 0,74036868 |
| -0,83539 | -0,835392 |
| -15,9733 | -15,973304 |
| 2,092881 | 2,09288061 |
| -0,49118 | -0,4911809 |
| 0,316078 | 0,31607779 |
Посчитаем дисперсию для каждого уравнения:
| D(x1) | D(x2) |
| 46,05336 | 5,369862 |
Формула будет иметь вид: =O55/(A54-1)
Далее посчитаем корреляционный момент (коэффициент ковариации) по формуле:
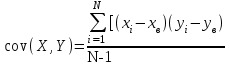
Для вычислений коэффициента введем еще 3 столбца с промежуточными расчетами и итоговой суммой под столбцом.