Файл: Связи и массовых коммуникаций российской федерации федеральное государственное.docx

x1-x1 cp	x2-x2 cp	(x1-x1 cp)*(x2-x2 cp)
-0,81406	16,36096442	-13,31881329
-4,93955	47,1471624	-232,8859639
3,010222	46,64249366	140,4042473
-0,11223	50,83580917	-5,705216513
0,740369	48,00739471	35,54317156
-0,83539	48,22782896	-40,28914485
-15,9733	49,94570095	-797,7978729
2,092881	47,88467131	100,2169
-0,49118	51,47049364	-25,28132206
0,316078	49,76824668	15,73063723
-1,04272	-10,8910285	11,35630811
8,061457	48,88530071	394,0867717

Проведем вычисления коэффициента корреляции по выражению:

---

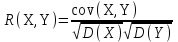D(x1)	46,05336
D(x2)	5,369862
cov(x1,x2)	19,11830144
R (x1,x2)	1,215729959

Где формула R(x1, x2) будет иметь вид: =Q55/(КОРЕНЬ(M3)*КОРЕНЬ(N3))

Проведем проверку вычисленного значения встроенной функцией КОРЕЛЛ.

КОРРЕЛ

0,008968061

Где, формула для вычислений для столбцов x1 и x2 будет иметь вид: =КОРРЕЛ(J3:J54;I3:I54)

Вычисленные значения совпадают.

Для оценки тесноты, или силы, корреляционной связи обычно используют общепринятые критерии, согласно которым абсолютные значения rxy < 0.3 свидетельствуют о слабой связи, значения rxy от 0.3 до 0.7 - о связи средней тесноты, значения rxy > 0.7 - о сильной связи.

Более точную оценку силы корреляционной связи можно получить, если воспользоваться таблицей Чеддока:

Абсолютное значение rxy	Теснота (сила) корреляционной связи
менее 0.3	слабая
от 0.3 до 0.5	умеренная
от 0.5 до 0.7	заметная
от 0.7 до 0.9	высокая
более 0.9	весьма высокая

Полученное значение коэффициента корреляции <0.3, следовательно, между выражениями слабая корреляционная связь.

Найдем значение t-критерия для оценки статистической значимости корреляционной связи по формуле:



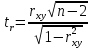
Полученное значение tr сравнивается с критическим значением при определенном уровне значимости и числе степеней свободы n-2. Если tr превышает tкрит, то делается вывод о статистической значимости выявленной корреляционной связи.

Tr	1,149145378
Критическое значение tкрит найдем по таблице критических значений корреляции Пирсона
к=n-2	50	число степеней свободы
р	0,01	уровень значимости
tкрит	0,451	по таблице корреляции Пирсона
ИТОГ	Статистически значимо	если Тр больше Ткрит то связь является статистически значимой

---

Задание 5.2.
Выполнение задания 5.2. будем проводить аналогично выполнению задания 5.1. с поправкой на a2, заданное с интервалом 0.25, 0.5, 0.75….4.0.

Модуль подсчета в среде MS Excel будет выглядеть следующим образом:

N=52		Дано						Уравнение 1	Уравнение 2
i	ti	A1	А2	w1	w2	a1	a2	х1	x2
1	1	0	50	480	480	0	0,25	-0,742317023	49,25768298
2	2	0	50	480	480	0	0,5	-2,347225118	47,65277488
3	3	0	50	480	480	0	0,75	-2,047080428	47,95291957
4	4	0	50	480	480	0	1	4,941031657	54,94103166
5	5	0	50	480	480	0	1,25	0,550559816	50,55055982
6	6	0	50	480	480	0	1,5	-0,661367124	49,33863288
7	7	0	50	480	480	0	1,75	-2,022065746	47,97793425
8	8	0	50	480	480	0	2	-0,217004877	49,78299512
9	9	0	50	480	480	0	2,25	-1,176793495	48,82320651
10	10	0	50	480	480	0	2,5	1,321234241	51,32123424
11	11	0	50	480	480	0	2,75	5,850996656	55,85099666
12	12	0	50	480	480	0	3	-4,972514788	45,02748521
13	13	0	50	480	480	0	3,25	-0,625919561	49,37408044

---

Выведем столбцы со средними значениями и разницу x1 – x1ср, x2 – x2ср,

x1 ср	x2 cp	x1-x1 cp	x1-x1 cp^2	(x1-x1 cp)*(x2-x2 cp)
0,270288	50,2702883	-1,01261	-0,8153728	1,02536949
		-2,34723		-111,8517901
		-2,04708		-98,16348314
		4,941032		271,4653767
		0,55056		27,8311069
		-0,66137		-32,63094974
		-2,02207		-97,0145374
		-0,217		-10,80315275
		-1,17679		-57,45483181
		1,321234		67,807372
		5,850997		326,7839947
		-4,97251		-223,8998361
		-0,62592		-30,90420274
		-1,10955		-54,24625936
		0,855602		43,51216176
		1,782071		92,27931581

---

Проведем вычисления коэффициента корреляции по выражению:

D(x1)	-0,73490958
D(x2)	50,27028828
cov(x1,x2)	1090,8247
R (x1,x2)	0,15009

Выполним проверку:

КОРРЕЛ

0,15

Результаты совпадают, следовательно, вычисления проведены правильно.

Поскольку значение коэффициента корреляции <0.3 имеем дело со слабой корреляционной связью.

Найдем значение t-критерия для оценки статистической значимости корреляционной связи.

Найдем значение t-критерия для оценки статистической значимости корреляционной связи:
Tr	1,073453301
Вывод	Слабая корреляционная связь
Критическое значение tкрит найдем по таблице притических значений корреляции Пирсона
к=n-2	50	число степеней свободы
р	0,01	уровень значимости
tкрит	0,451	по таблице корреляции Пирсона
ИТОГ	Статистически значимо		если Тр больше Ткрит то связь является статистически значимой

Таким образом, мы исследовали возможность обработки сигналов в среде MS Excel, оценивали их взаимосвязь и статистическую значимость. Отмечается, что, хотя на первый взгляд выражения кажутся похожими, на самом деле они имеют мало общего из-за разницы в значении переменных. Тем не менее, даже небольшая связь может быть статистически значимой.

---