Файл: Проектирование цифрового арифметикологического устройства на интегральных микросхемах.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 83
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- 1 2 3 4 5 6 7 8
Разработка схемы логической операции “ ”
”
Данная схема является самой простой в данной курсовой работе.
Чтобы реализовать данную схему над двумя 32-разряжными операндами достаточно выполнить эту операцию побитно над каждыми i-м разрядами операндов. Для этого используются вентили «ИЛИ», после которых сигналы поступают на вентиль «НЕ», тем самым инвертируя операцию «ИЛИ»
В пункте “Описание разработанного устройства” упоминалось, что выходы у арифметической и у логической схемы общие, и для определения какой из моделей должен быть включен используются выходные буферы, реализованные при помощи микросхем 74HC245.
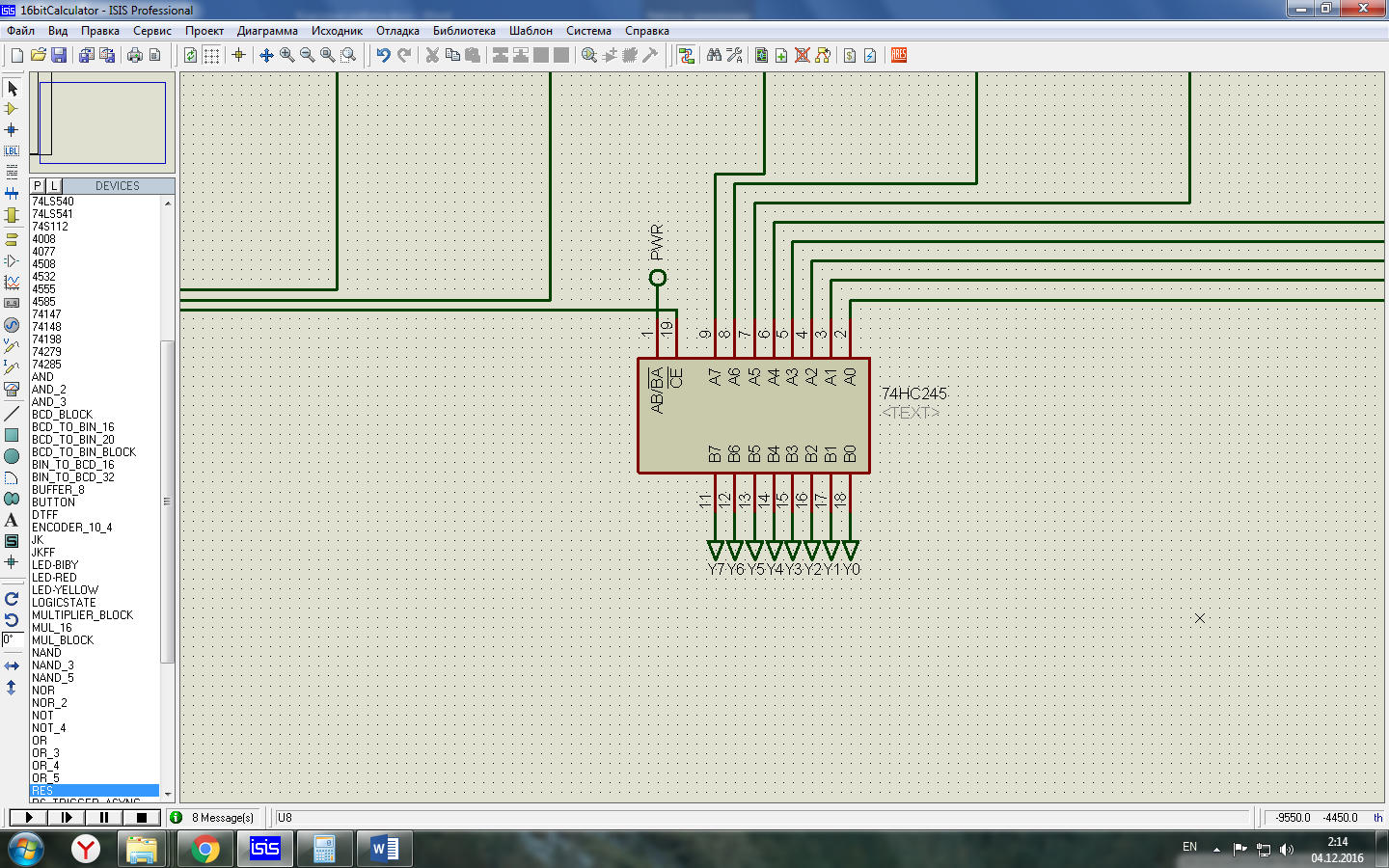
Рисунок 2.1. Пример выполнения выходного буфера с использованием микросхемы КР 74HC245 АП6.
Для выполнения операции “

Рисунок 2.2. Вид блока логической операции “Исключающее ИЛИ” для 16-разрядных операндов.
Полная схема блока “

Рисунок 2.2.1 Результат работы
-
Разработка схемы арифметической операции “Умножение”
Наиболее просто умножение выполняется в прямом коде, независимо от того, являются ли операнды целыми или дробными числами. В ЭВМ с фиксированной точкой умножение реализуется в два этапа.
Первый этап заключается в определении знака произведения с помощью сложения знаковых цифр сомножителей по модулю два, где 0 – соответствует плюсу, а 1 – минусу (табл. 2.1.1).
Таблица 2.1.1.
Сложение по модулю два
-
X1
X2
Y
0
0
0
0
1
1
1
0
1
1
1
0
По-другому, это эквивалентно
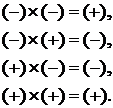
На втором этапе производится перемножение модулей сомножителей, затем в случае необходимости округления полученного модуля произведения, после чего к модулю результата приписывается его знак, определенный на первом этапе.
Умножение производится по обычным правилам арифметики, согласно двоичной таблицы умножения (табл. 2.1.2).
Таблица 2.1.2.
Таблица умножения
-
X1
X2
Y
0
0
0
0
1
0
1
0
0
1
1
1
Рисунок 2.7. Схема операции «Сложение»
Рассмотрим пример умножения двоичных чисел в ЭВМ.
Выполнить умножение чисел A = 101112 и B = 1012 в двоичной системе счисления.
Умножение выполняется в несколько этапов:
1. Впишем множимое A, допустим в 8-ми разрядный регистр, начиная с младших разрядов (нумерация разрядов начинается с нуля). В недостающие разряды записываем нули.
2. Впишем множитель В в 8-ми разрядный регистр, начиная с младших разрядов. В недостающие разряды записываем нули.

3. Подготовим (обнулим) регистр результата C удвоенной разрядности (16 бит). Произведение содержит в два раза больше разрядов чем исходные сомножители.
4. Дальше выполняется следующий цикл:
4.1. Анализируем очередной разряд множителя В (начинаем с младших), если он "1", то прибавляем множимое A к старшим разрядам регистра С, результат снова в С. Если очередной разряд множителя "0", пропускаем данный шаг.
4.2. Сдвигаем содержимое регистра С на один разряд вправо. При этом крайний левый (старший) разряд заполняется нулем. Но
если перед этим была операция сложения, во время которой возник перенос из старшего разряда, то тогда крайний левый разряд заполняется единицей.
4.3. Действия, описанные в п. п. 5.1 и 5.2,повторяютсядо тех пор не будут проанализированы все разряды множителя.
В итоге процесс умножения выглядит следующим образом:

где «+А» - числоА прибавляется к регистру C; «-->»содержимое регистра C сдвигается на один разряд вправо; «=» - показывается значение частичного произведения полученного после сложения, которое заносится в регистр С.
5. Определяется знак результата. Если знаки исходных сомножителей одинаковы, то результирующее произведение положительно и наоборот. В данном случае знаки совпадают, следовательно результирующее произведение положительно.
В итоге получается ответ:
Ниже приведены схемы полусумматора, полного сумматора и фрагмента схемы вычитания в программе Proteus
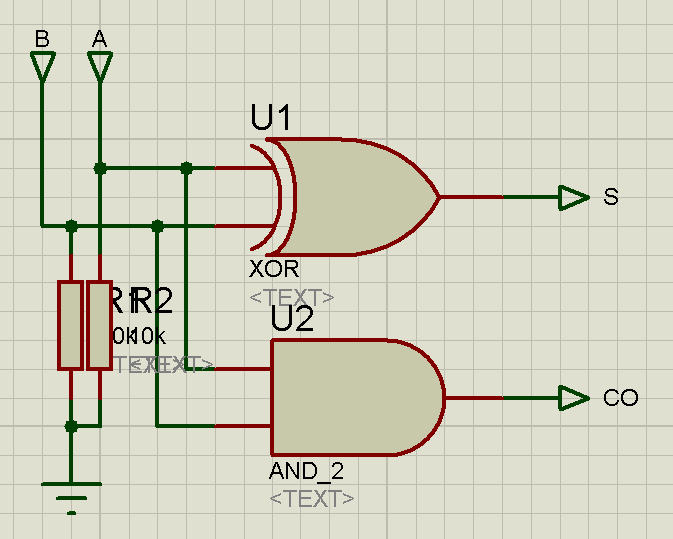
Рисунок 2.9. Схема блока полусумматора в программе Proteus
Входы схемы подтянуты к земле через 10 КОм резисторы для однозначного определения низкого уровня на входах, при отсутствии поступающих сигналов.
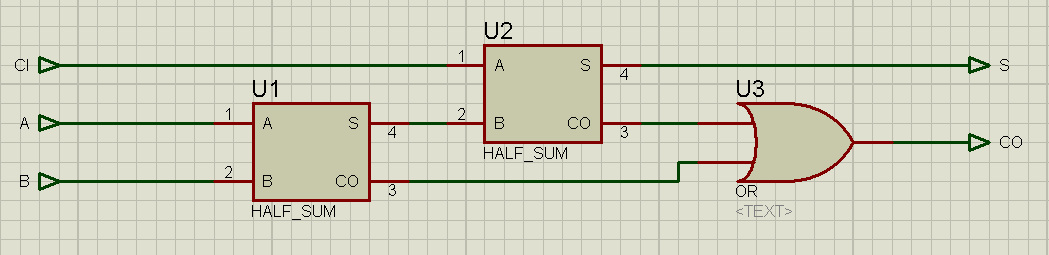
Рисунок 2.10. Схема блока полного сумматора в программе Proteus
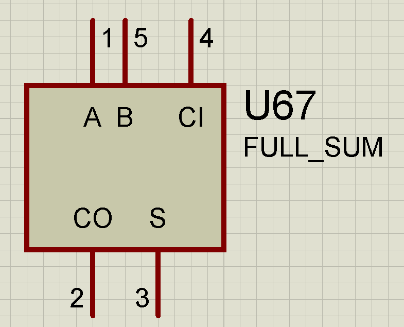
Рисунок 2.11. Вид блока полного сумматора в программе Proteus
Для наглядности вся схема вычитания была помещена в блок вычитания (рис. 5.). Выходные буферы также помещены внутрь данного блока. Включение выходных буферов осуществляется через вход OE.

Рисунок 2.12. Вид блока полного сумматора в программе Proteus
Полная схема арифметической операции “Умножение” была создана на основе схем вышеописанных блоков по и приведена в Приложении 1.
Рисунок 2.12.1 Результат работы
- 1 2 3 4 5 6 7 8