Файл: Методы расчета показателей надежности сжат.docx

3.2 Расчет надежности комбинационных схем

Исходные данные:

Вариант 14
Функция алгебры логики

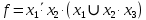
Значение вероятностей появления входных переменных:








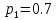
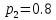
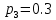
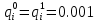
С помощью логической функции, заданной в алгебраическом виде построим комбинационную схему на двухвходовых логических элементах (рис.1):



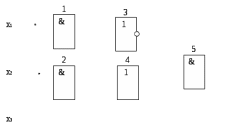
Рис.1 Комбинационная схема

Для анализа комбинационной схемы построим таблицу истинности (табл. 1)

Таблицу истинности построим по логической формуле ФАЛ. Для этого в логическую формулу функции нужно подставить все возможные значения входных переменных и вычислить значения функции.

Таблица 1

S	x1	x2	x3	f
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	1
5	1	0	1	1
6	1	1	0	0
7	1	1	1	0

При расчетах надежности принимается допущение об одиночных константных неисправностях. Неисправность логического элемента приводит на выходе элемента к отказам двух видов:

---

- ложное появление сигнала 1 вместо 0.

- ложное появление сигнала 0 вместо 1.



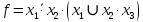
y1 = 0,

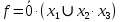
y1 = 1,

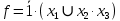
y2 =0,

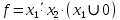
y2 = 1,

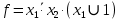
y3 = 0,

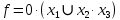
y3 = 1,

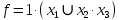
y4 = 0,

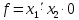
y4 = 1,

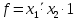
y5 = 0, f =

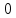
y5 = 1, f =

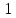
По полученным формулам построим таблицу неисправностей (табл. 2.), где 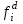- функция, реализуемая схемой при неисправности i-го логического элемента типа d.

Таблица 2

S	x1	x2	x3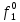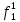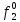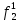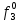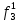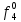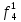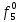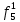
0	0	0	0	0	0	0	1	0	0	0	1	0	1
1	0	0	1	0	0	0	1	0	0	0	1	0	1
2	0	1	0	0	0	0	1	0	0	0	1	0	1
3	0	1	1	1	0	0	1	0	1	0	1	0	1
4	1	0	0	1	0	1	1	0	1	0	1	0	1
5	1	0	1	1	0	1	1	0	1	0	1	0	1
6	1	1	0	1	0	0	0	0	1	0	0	0	1
7	1	1	1	1	0	0	0	0	1	0	0	0	1

---

Введем понятие функции ошибки 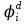. (табл.3) Эта функция выделяет те наборы , для которых неисправность является существенной.

Так как по определению 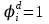, если 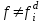, то тогда определение соответствует формуле: .

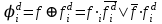Таким образом, в соответствии с определением функция ошибки равна 1 для наборов, на которых неисправность является существенной.

Таблица 3

S	x1	x2	x3	f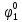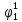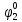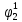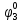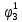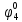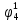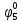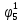
0	0	0	0	0	0	0	0	1	0	0	0	1	0	1
1	0	0	1	0	0	0	0	1	0	0	0	1	0	1
2	0	1	0	0	0	0	0	1	0	0	0	1	0	1
3	0	1	1	1	0	1	0	0	1	0	1	0	1	0
4	1	0	0	1	0	1	0	0	1	0	1	0	1	0
5	1	0	1	1	0	1	0	0	1	0	1	0	1	0
6	1	1	0	0	1	0	0	0	0	1	0	0	0	1
7	1	1	1	0	1	0	0	0	0	1	0	0	0	1

---

Произведя подобные вычисления для сбоев типа 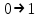и 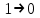всех пяти элементов схемы, получим:

φ1 = {6,7}; φ1 = {3,4,5}; φ2 = {-}; φ2 = {0,1,2}; φ3 = {3,4,5}; φ3 = {6,7}

φ4 = {3,4,5}; φ4 = {0,1,2}; φ5 = {3,4,5}; φ5 = {1,2,3,6,7};

При расчете надежности следует учитывать, что вероятность отказа элемента зависит не только от характера неисправности - n_{i ,} но и от вероятности появления входных наборов.

Определим вероятности R_k появления входных наборов.

Появление всех входных наборов составляет полную группу событий, поэтому



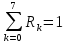
где k – номера входных наборов.

Составим таблицу, отражающую полную группу событий на входе схемы.

Результаты расчета приведены в таблице 4.







Таблица 4

S	x1	x2	x3	f	Rk
0	0	0	0	1	R0= (1-p1)(1-p2)(1-p3) = 0,3 * 0,2 * 0,7 = 0,042
1	0	0	1	1	R1 = (1-p1)(1-p2)p3= 0,3 * 0,2 * 0,3 = 0,018
2	0	1	0	0	R2 = (1-p1)p2(1-p3) = 0,3 * 0,8 * 0,7 = 0,101
3	0	1	1	1	R3 = (1-p1)p2p3 = 0,3 * 0,8 * 0,3 = 0,072
4	1	0	0	0	R4 = p1(1-p2)(1-p3) = 0,7 * 0,2 * 0,7 = 0,098
5	1	0	1	1	R5 = p1(1-p2)p3 = 0,7 * 0,2 * 0,3 = 0,042
6	1	1	0	1	R6 = p1p2(1-p3) = 0,7 * 0,8 * 0,7 = 0,392
7	1	1	1	1	R7 = p1p2p3 = 0,7 * 0,8 * 0,3 = 0,168

---

Определим вероятности истинности функций ошибки как условные вероятности того, что на выходе схемы происходит ошибка при наличии сбоя



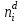
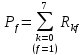
где 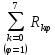- сумма вероятностей тех наборов, на которых функция .

В нашем случае:

P(φ₁) = R₆ +R₇ = 0,392+0,168=0,56

P(φ₁) = R₃+ R₄+ R₅= 0,072+0,098+0,042=0,212

P(φ₂) = -

P(φ₂) = R₀ + R₁ +R₂= 0,042+0,018+0,101=0,161

P(φ₃) = R₃+ R₄+ R₅= 0,072+0,098+0,042=0,212

P(φ₃) = R₆ +R₇ =0,392+0,168=0,56

P(φ₄) = R₃+ R₄+ R₅= 0,072+0,098+0,042=0,212

P(φ₄) = R₀ + R₁ +R₂= 0,042+0,018+0,101=0,161

P(φ₅) = R₃+ R₄+ R₅= 0,072+0,098+0,042=0,212

P(φ₅) = R₀ + R₁ +R₂ +R₆ +R₇ =0,042+0,018+0,101+0,392+0,168=0,721

Далее необходимо определить вероятность появления неисправности в момент времени.

Допустим, что вероятности сбоев 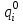и 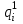для всех элементов одинаковые и равны:



В этом случае:

Q₁ = 0,001 * 0,56 = 56 ∙ 10^-5

Q₁ = 0,001 * 0,212= 21,2 ∙ 10^-5

Q₂ = -

Q₂ = 0,001 * 0,161 = 16,1 ∙ 10^-5

Q₃ = 0,001 * 0,212 = 21,2 ∙ 10^-5

Q₃ = 0,001 * 0,56 = 56 ∙ 10^-5

Q₄ = 0,001 * 0,212 = 21,2 ∙ 10^-5

Q₄ = 0,001 * 0,161 = 16,1 ∙ 10^-5

Q₅ = 0,001 * 0,221 = 22,1 ∙ 10^-5

Q₅ = 0,001 * 0,721 = 72,1 ∙ 10^-5

Вероятность ошибки на выходе схемы в момент времени t определяется по следующей формуле:



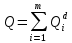
Для нашего примера:

Q = (56+21,2+16,1+21,2+56+21,2+16,1+22,1+72,1) ∙ 10^-5 = 302 ∙ 10^-5

Соответственно, вероятность отсутствия ошибки на выходе схемы, т.е. вероятность исправной работы схемы равна:

P = 1 – Q

P = 1 – 302*10^-5 = 0,99698

---