Добавлен: 23.11.2023
Просмотров: 243
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. Особенности надежности и безопасности СЖАТ
2. Показатели надёжности для невосстанавливаемых и восстанавливаемых систем
3. Методы расчета показателей надежности СЖАТ
3.1 Статистические оценки показателей надежности
3.2 Расчет надежности комбинационных схем
3.3 Расчет показателей надежности восстанавливаемых систем методом Марковских процессов
3.6 Расчет эксплуатационной надежности СЖАТ
5. Способы повышения надежности и безопасности устройств и систем ЖАТ
3.3 Расчет показателей надежности восстанавливаемых систем методом Марковских процессов
Исходя из значений интенсивностей отказов
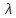 ???? и интенсивностей восстановления
???? и интенсивностей восстановления 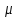 ????, найти параметры надежности (предполагая простейший поток отказов): финальные вероятности нахождения системы во всех состояниях Рi , в том числе вероятность отказа системы Qc ; время наработки на отказ Tcp и интенсивность отказов системы
????, найти параметры надежности (предполагая простейший поток отказов): финальные вероятности нахождения системы во всех состояниях Рi , в том числе вероятность отказа системы Qc ; время наработки на отказ Tcp и интенсивность отказов системы 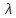 c ; среднее время восстановления Tв; коэффициент готовности Кг ; среднее время безотказной работы системы (среднюю наработку до отказа) Тот.
c ; среднее время восстановления Tв; коэффициент готовности Кг ; среднее время безотказной работы системы (среднюю наработку до отказа) Тот.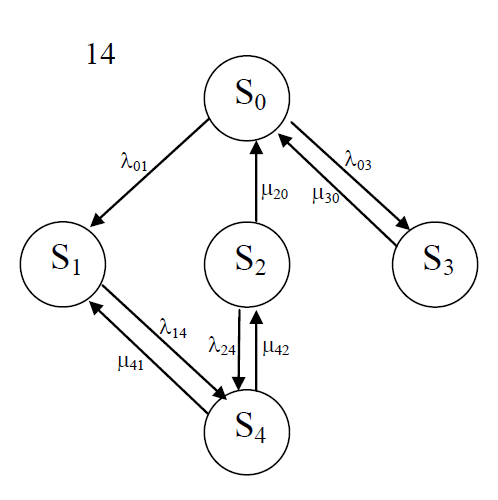
Рис.6. Граф состояний
Исходя из графа, система может находиться в одном из 5 состояний:
0 – исправное состояние;
1 – 1-е работоспособное состояние: отказал первый элемент (находится в ремонте), второй и третий – исправны;
2 - 2-е работоспособное состояние: отказал второй элемент (находится в ремонте), первый и третий – исправны;
3 – 3-е работоспособное состояние: отказал третий элемент (находится в ремонте), первый и второй – исправны;
4 – неработоспособное состояние (состояние отказа): отказали последовательно все элементы и находятся в состоянии ремонта.
Интенсивность отказов
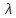 ????????=
????????=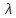 =
= 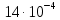 1/ч, интенсивность восстановления
1/ч, интенсивность восстановления 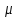 ????????=
????????=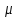 =0,7142, 1/ч.
=0,7142, 1/ч.Составим систему уравнений Колмогорова для финальных вероятностей нахождения во всех состояниях:
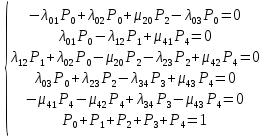
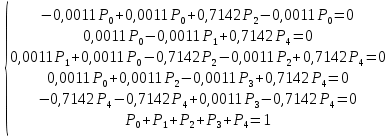
Решим систему и получим значения финальных вероятностей:
Система состоит из шести уравнений, пять неизвестных, значит можно путем подстановки выразить каждую переменную:
Р0=0,355
P1=0,131
P2=0,487
P3=0,025
P4=0,002
Вероятность отказа системы:
QC=P4=0,00018
Вероятность безотказной работы:
PC=1-QC=1-0,00018=0,99982
Время наработки на отказ:
Tср=
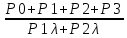 =
=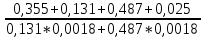 =897,1 ч.
=897,1 ч.Интенсивность отказов:
λc=1/ Tср=1/897,1 = 0,00111 1/ч.
Среднее время восстановления:
Tв=
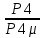 =
=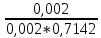 =1,40
=1,40Коэффициент готовности:
Кг=
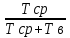 =
=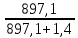 =0,999
=0,999Для нахождения среднего времени безотказной работы выполним преобразование Лапласа для уравнений Колмогорова с учетом начальных условий:
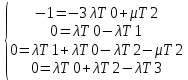 →
→ 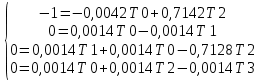
Система состоит из четырех уравнений, 3 неизвестных, значит можно путем подстановки выразить каждую переменную:
T0=714,3 ч.
T1=714,3 ч.
T2=2,2 ч.
T3=717 ч.
Среднее время безотказной работы системы:
Tот=T0+T1+T2+T3=714,3+714,3+2,2+717=2147,8 ч.
3.4 Структурный метод расчета надежности
Задана последовательно-параллельная схема расчёта надёжности. Так же задана интенсивность отказов для каждого i-ого элемента, время восстановления узла и время работы t=1год.
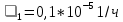 ,
, 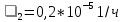 ,
, 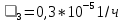 ,
, 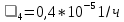 ,
, 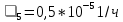 , и
, и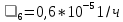 ,
, 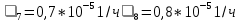 ,
, 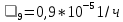
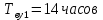 ,
, 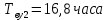 ,
, 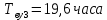
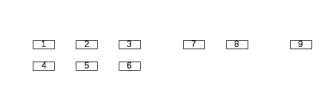
Рис.7.
Логическая функция схемы:
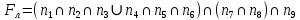
Арифметическая функция:
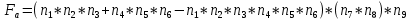
Преобразуем узлы схемы:
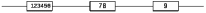
Рис.8.
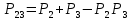
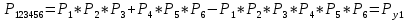
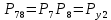
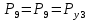
Функция надежности:
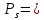
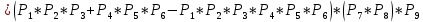
Значения функции надёжности схемы за t=1 год (8760 ч):
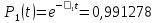
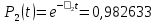
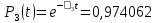
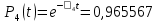
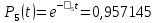
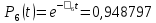
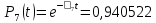
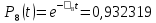
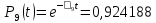
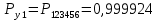
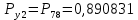
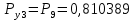
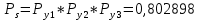
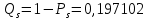
Интенсивностьотказов:
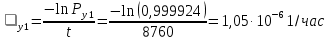
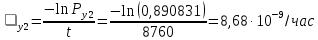
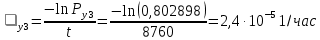
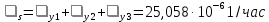
Среднее время наработки до отказа:
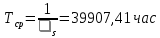
Среднее время восстановления системы:
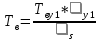
+
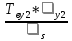 +
+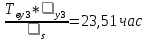
Коэффициент готовности:
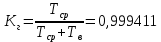
Вывод: после определения всех параметров системы можно сделать вывод, что система в течении года будет работать надёжно с вероятностью 99.94%
3.5 Топологический метод расчета надежности резервированных систем
Топологическими называются методы, которые позволяют определить показатели надежности либо по графу состояний, либо по структурной схеме системы без составления и решения уравнений. Как и любые другие методы расчета надежности, они имеют свои ограничения:
-
интенсивности отказов и восстановления элементов сложной системы являются величинами постоянными, другими словами, время наработки на отказ и время восстановления распределены по экспоненциальному закону; -
топологические методы нельзя использовать для многосвязных графов.
Дана система, состоящая из трех последовательно включенных блоков.
Рис.9.
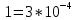 1/ч,
1/ч, 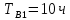
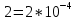 1/ч,
1/ч,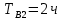
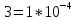 1/ч,
1/ч,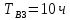
Обслуживанием занимается одна ремонтная бригада (r = 2).
Найдем время наработки на отказ системы без резервирования. Для экспоненциального закона распределения интенсивностей отказов и восстановлений получим:
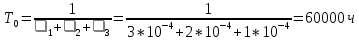

Время наработки на отказ системы без резервирования:
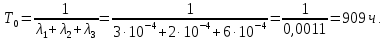
-
Интенсивность отказа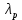 и интенсивность восстановления
и интенсивность восстановления 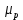 .
.
Если все элементы системы идентичны по безотказности и ремонтопригодности, то функционирование систем с постоянно включённым резервом, резервом замещением, с мажоритарным резервированием и скользящим резервом, обслуживаемых любым количеством ремонтных бригад, будет описываться графом, показанным на рис. 3.

Рис. 3. Граф состояний резервированной системы с идентичными элементами
Приняты следующие обозначения:
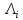 – интенсивности переходов, соответствующие отказам элементов системы,
– интенсивности переходов, соответствующие отказам элементов системы, 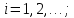
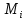 – интенсивности переходов, соответствующие восстановлениям элементов системы.
– интенсивности переходов, соответствующие восстановлениям элементов системы.Воспользуемся таблицей 2 и приведёнными ниже формулами:
-
наработка на отказ:
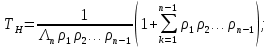
где
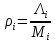
-
среднее время восстановления:
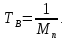
-
интенсивность восстановления
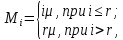
где r – число ремонтных бригад.
Интенсивность отказа первой системы после резервирования определяется по формуле в соответствии с таблицей 2 для постоянного резервирования:
Найдем интенсивность отказа и интенсивность восстановления первого элемента после резервирования ????1р и μ1р.
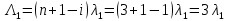
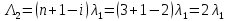
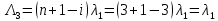
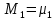
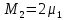
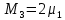
где
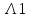 ,
,