ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.11.2023
Просмотров: 20
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Оглавление
Введение 2
Постановка задачи 3
Решение задачи 6
Выводы 8
Литература 9
Введение
Предпочтениемлица, принимающего решения (ЛПР) выраженное каким-либо образом его личное суждение о наличии или отсутствии преимущества одного из вариантов по отношению к другому варианту или ко всем остальным вариантам, либо в целом, либо по некоторым отдельным характеристикам разработана методология и ряд технологий, позволяющих более гибко извлекать знания из ЛПР, и компактно хранить их в виде структурных и параметрических элементов экономико-математических моделей. При этом построенные модели оказываются хорошо согласованными с целевыми установками ЛПР, что вызывает доверительное отношение ЛПР к решениям, принимаемым в системе.
Предлагаемая методология позволяет подстраивать такие модели в условиях изменчивости среды и/или предпочтений ЛПР. Построенные таким образом модели представляют собой экспертные знания опытных ЛПР в соответствующей предметной области. Поскольку такие модели работают на некотором поле исходных ситуаций, требующих принятия решений, а на выходе формируются готовые решения, то знания, хранящиеся в подобных моделях, могут отчуждаться от их первоначального источника (ЛПР) и использоваться в дальнейшем несколькими способами.
Рассмотрим класс моделей линейного программирования, используемых в качестве основы процедур распределения ограниченных ресурсов на оперативном горизонте планирования в производственных системах, приведена технология эффективного взаимодействия системы с ЛПР для извлечения из него необходимых знаний. Указанные модели входят в состав систем поддержки принятия решений (СППР) комплексных информационных систем (КИС) предприятий. Если условия применения моделей выполняются, и они оказываются эффективными, то в ряде случаев бывает желательно ускорить процесс настройки параметров целевой функции. Для пользователя всегда желательно, чтобы процесс итерационной настройки был бы как можно короче, а точность настройки модели была бы как можно выше. Эти требования взаимосвязаны и противоречивы, однако в ряде практических случаев их можно, в той или иной степени, выполнить.
Постановка задачи
Пусть в СППР для выбора решений используется задача линейного программирования (ЗЛП) на максимум:
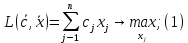
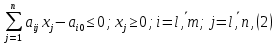 где c, x – вектор параметров целевой функции и вектор переменных. Ограничения (2), образующие область допустимых решений (ОДР) и приводящие к необходимости выбора решения, названы ситуацией, требующей принятия решения (СТПР). Они обычно автоматически формируются из данных учетных систем предприятия. Априорная неопределенность задачи (1)-(2) заключается в том, что реально менеджер принимает во внимание не один, а несколько критериев, поэтому коэффициент c , как векторная свертка, не известен. Задачу (1)-(2) будем называть прямой ЗЛП (ПЗЛП). На фазе настройки (обучения) модели по тем предъявлениям (2), для которых принятое ЛПР решение (после их реализации) признано «хорошим», решается обратная ЗЛП (ОЗЛП) с помощью, например, итерационной процедуры, построенной на основе метода наименьших квадратов [3], в результате чего вычисляются оценки
где c, x – вектор параметров целевой функции и вектор переменных. Ограничения (2), образующие область допустимых решений (ОДР) и приводящие к необходимости выбора решения, названы ситуацией, требующей принятия решения (СТПР). Они обычно автоматически формируются из данных учетных систем предприятия. Априорная неопределенность задачи (1)-(2) заключается в том, что реально менеджер принимает во внимание не один, а несколько критериев, поэтому коэффициент c , как векторная свертка, не известен. Задачу (1)-(2) будем называть прямой ЗЛП (ПЗЛП). На фазе настройки (обучения) модели по тем предъявлениям (2), для которых принятое ЛПР решение (после их реализации) признано «хорошим», решается обратная ЗЛП (ОЗЛП) с помощью, например, итерационной процедуры, построенной на основе метода наименьших квадратов [3], в результате чего вычисляются оценки 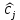 координат вектора
координат вектора 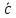 . Так, если воспользоваться стохастическим рекуррентным алгоритмом оценивания, то он кратко может быть представлен в таком виде:
. Так, если воспользоваться стохастическим рекуррентным алгоритмом оценивания, то он кратко может быть представлен в таком виде: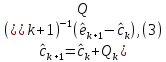
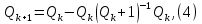
где k – номер шага итерационной процедуры;
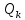 – дисперсионная матрица оценок вектора целевой функции;
– дисперсионная матрица оценок вектора целевой функции; 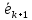 – суммарный вектор (единичной длины), соответствующий гиперплоскостям образующих крайнюю точку ОДР, выбранную ЛПР в качестве оптимальной в (k+1)-м наблюдении. В подобных алгоритмах начальное значение искомого вектора обычно принимают минимально возможным, а элементы (диагональные) дисперсионной матрицы – максимально возможными. Бизнес-процессы организационно экономических систем, в которых используется модель (1), (2), делятся на две группы: на такие, которые допускают вмешательство
– суммарный вектор (единичной длины), соответствующий гиперплоскостям образующих крайнюю точку ОДР, выбранную ЛПР в качестве оптимальной в (k+1)-м наблюдении. В подобных алгоритмах начальное значение искомого вектора обычно принимают минимально возможным, а элементы (диагональные) дисперсионной матрицы – максимально возможными. Бизнес-процессы организационно экономических систем, в которых используется модель (1), (2), делятся на две группы: на такие, которые допускают вмешательствов формирование ограничений (2),
предъявляемых ЛПР для выбора решений, и на такие, которые не оставляют этой возможности. Для второй группы ускорить процесс настройки не представляется возможным, а для первой существуют два варианта: первый – сформировать ограничения (2) оптимальным (в смысле максимизации прироста информации о векторе
 ) способом; второй – не изменяя реально возникших ограничений (2), скомпоновать из них такие отдельные подмножества, которые, будучи предъявленными ЛПР, позволят получить максимальный прирост информации о векторе
) способом; второй – не изменяя реально возникших ограничений (2), скомпоновать из них такие отдельные подмножества, которые, будучи предъявленными ЛПР, позволят получить максимальный прирост информации о векторе  . Первый способ назван активным экспериментом над ЛПР, а второй полуактивным. Термин «эксперимент над ЛПР» имеет смысл, т.к. означает взаимодействие с ЛПР как со звеном системы управления бизнес-процессами, характеристики которого необходимо измерить (оценить).
. Первый способ назван активным экспериментом над ЛПР, а второй полуактивным. Термин «эксперимент над ЛПР» имеет смысл, т.к. означает взаимодействие с ЛПР как со звеном системы управления бизнес-процессами, характеристики которого необходимо измерить (оценить).Решение задачи
Для описания вариантов ускорения процесса выявления предпочтений ЛПР введем ряд терминов, описывающих взаимодействие среды (генерирующей ситуации), ЛПР и модели.
В ПЗЛП оптимальные крайние точки области допустимых решений (ОДР) несут различный объем информации о целевой функции. Телесный угол, образованный пучком гиперплоскостей, определяет степени свободы для гиперплоскости ЦФ – чем больше угол, тем более определенным является положение ЦФ. Этот показатель будем называть информативностью СТПР – ϕ . Поскольку априори неизвестно, на какой из вершин будет достигнут оптимум, то, в идеале, желательно иметь ОДР в виде симметричного многогранника, близкого к сфере (гиперсфере).
Способность ЛПР быстро «переварить» некоторое количество ограничений будем называть пропускной способностью ЛПР –
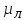 . А его возможность различать альтернативы, расположенные в различной степени удаления друг от друга, будем называть разрешающей способностью ЛПР –
. А его возможность различать альтернативы, расположенные в различной степени удаления друг от друга, будем называть разрешающей способностью ЛПР – 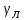 . Если ЛПР обладает высокой пропускной и разрешающей способностью, то при достаточно информативной СТПР его предпочтения в рамках рассматриваемого подхода могут быть выявлены практически за один шаг. По аналогии с пропускной способностью ЛПР будем говорить и о плотности потока альтернатив, предъявляемых ЛПР (или просто плотности альтернатив – λ ), и понимать под этим количество вершин ОДР в одном предъявлении. Поскольку настраиваемая модель является отражением предпочтений ЛПР, то введем и термин разрешающей способности модели –
. Если ЛПР обладает высокой пропускной и разрешающей способностью, то при достаточно информативной СТПР его предпочтения в рамках рассматриваемого подхода могут быть выявлены практически за один шаг. По аналогии с пропускной способностью ЛПР будем говорить и о плотности потока альтернатив, предъявляемых ЛПР (или просто плотности альтернатив – λ ), и понимать под этим количество вершин ОДР в одном предъявлении. Поскольку настраиваемая модель является отражением предпочтений ЛПР, то введем и термин разрешающей способности модели –
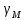 .
. Таким образом, информативность СТПР и плотность альтернатив – это характеристики внешней (по отношению к ЛПР) среды. Разрешающая и пропускная способности ЛПР являются характеристиками, от которых зависит качество принимаемых решений. Разрешающая способность модели отражает ее качество как звена выбора решений. Если разрешающая способность модели не хуже разрешающей способности ЛПР и оценки
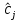 не смещены относительно
не смещены относительно  , то модель адекватна предпочтениям ЛПР.
, то модель адекватна предпочтениям ЛПР. Процесс адаптивной настройки модели может быть ускорен на основе применения методов планирования оптимальных экспериментов [4]. Эксперименты над ЛПР (зондирование ЛПР) можно проводить с двумя целями: для выявления предпочтений ЛПР (решение ОЗЛП для построения оценок
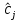 ); для тестирования ЛПР (оценивание его характеристик
); для тестирования ЛПР (оценивание его характеристик  и
и  ). Возможна и комбинация этих целей, однако здесь рассмотрим лишь первую из них. При этом будем полагать, что характеристики
). Возможна и комбинация этих целей, однако здесь рассмотрим лишь первую из них. При этом будем полагать, что характеристики  и
и  априори неизвестны, а значит в соответствии с принципом минимизации данных в каждом предъявлении и для обеспечения максимальной контрастности альтернатив в предъявлении активный и полуактивный эксперименты должны быть организованы следующим образом (покажем на примере двух переменных).
априори неизвестны, а значит в соответствии с принципом минимизации данных в каждом предъявлении и для обеспечения максимальной контрастности альтернатив в предъявлении активный и полуактивный эксперименты должны быть организованы следующим образом (покажем на примере двух переменных). Активный эксперимент (см. рис.1 а). Предъявления выполняются по шагам. На каждом шаге для выбора решения добавляется по одному ограничению (пронумерованы: 1, 2, 3, …), обеспечивающему максимальную контрастность новых альтернатив. ЛПР на каждом шаге выбирает наилучшую альтернативу в пределах своей разрешающей способности, постепенно приближаясь к идеальной точке на вписанной сфере. Предъявления проводятся одним из двух способов: либо стандартными ограничениями (2), либо в виде набора альтернативных крайних точек ОДР.
Полуактивный эксперимент (см. рис. 1 б). Предъявления также выполняются по шагам, однако в каждом предъявлении ограничения выбираются из существующего набора (2). Эффект достигается за счет снижения нагрузки на ЛПР на каждом очередном шаге в предположении, что он обладает минимальными
 и
и  . Для примера, приведенного на рис. 1 б, число предъявляемых ограничений постепенно возрастает (1, 2, 3, ...), начиная с одного, вместо исходных семи. Следует отметить, что максимальную скорость решения ОЗЛП, т.е. получения эффективных оценок
. Для примера, приведенного на рис. 1 б, число предъявляемых ограничений постепенно возрастает (1, 2, 3, ...), начиная с одного, вместо исходных семи. Следует отметить, что максимальную скорость решения ОЗЛП, т.е. получения эффективных оценок  , обеспечивает активный эксперимент.
, обеспечивает активный эксперимент.Выводы
1. Предложены алгоритмы, существенно повышающие скорость и достоверность выявления предпочтений ЛПР для аппроксимации их линейной целевой функцией. Алгоритмы построены в соответствии с принципами планирования оптимального эксперимента.
2. Введены формальные характеристики ЛПР как звена системы управления предприятием, которые также могут быть оценены в рамках тестовых экспериментов. Измерение этих характеристик может быть использовано для мониторинга их соответствия требуемым значениям как пороговые уровни требований к ЛПР.
Литература
1. Ярушкина Н. Г. Основы теории нечетких и гибридных систем. – М.: Финансы и статистика, 2004. – 320 с.
2. Черноруцкий И.Г. Методы принятия решений. – СПб.: БХВ-Петербург, 2005. – 416 с.
3. Вилисов В.Я. Методы выбора экономических решений. – М.: Финансы и статистика, 2006. – 228 с. 4. Федоров В.В. Теория оптимального эксперимента. – М.: Наука, 1971. – 312 с.